机器学习吃瓜教程打卡班第一、二章
机器学习吃瓜教程打卡班第一、二章
- 绪论
-
- 基本概念
- 归纳
- NFL定律
- 模型评估
-
- 过拟合与欠拟合:
- 评估方法
-
- 留出法
- 交叉验证法
- 自助法
- 调参
- 性能度量
-
- 错误率与精度
- 混淆矩阵(Confusion Matrix)
- ROC与SUC
- 代价敏感错误率与代价敏感曲线
- 比较检验
-
- 假设检验
-
- 二项分布
第一二章的内容主要包含绪论及模型评估,通过对西瓜书的学习,对机器学习的概念有了初步认识,对机器学习的模型评估有了一定的了解。
绪论
基本概念
- 学习算法:机器学习所研究的内容是关于在计算机上从数据中产生模型的算法。 机器学习:通过计算的手段,利用经验改善系统自身的性能
- 示例/样本:每条关于一个事件或对象的描述记录; 属性/特征:反映事件或对象在某方面的表现或性质的事项,如“色泽”、“根蒂”……
- 属性值:属性上的取值,
- 属性空间/样本空间/输入空间:属性张成的空间;如把“色泽”、“根蒂”和“敲声”作为三个坐标轴,则它们张成一个用于描述西瓜的三维空间;
- 特征向量:一个事件或对象,即示例,因为空间中每个点对应一个坐标向量; 标记:关于示例结果的信息,如“好瓜”;
- 样例:拥有标记信息的示例,如 ((色泽=青绿;根蒂=蜷缩;敲声=浊响),好瓜) 标记空间/输出空间:所有标记的集合。
- 泛化能力:学得模型适用于新模型的能力。
归纳
机器学习在学习过程中对某种类型假设的偏好,称为“归纳偏好”或者简称为“偏好”。任何一个有效的机器学习算法必定有它的归纳偏好。
“奥卡姆剃刀”,是一种常用的、自然科学研究中最基本的原则,能够引导算法确立“正确的”偏好。即“若有多个假设与观察一致,则选最简单的那个”。那么怎么判定哪个假设更“简单”呢,这个问题需要借助其他机制才能解决。(简而言之,通过一定的标准,选最简单的)
NFL定律
没有免费午餐定理是说无论两种算法 La多聪明、Lb多笨拙,它们的期望性能竟然相同。
NFL定理的前提是:所有问题出现的机会相同、或者说所有的问题同等重要。
具体推导可见https://zhuanlan.zhihu.com/p/48493722
模型评估
不同的机器学习任务, 如分类(classification)、回归(regression)、排序(ranking)、聚类(clustering)、主题模型(topic modeling),有着不同的评价指标。
过拟合与欠拟合:
过拟合:把训练样本自身的特点当成所有潜在样本都会具有的一般性质
欠拟合:对训练样本的一般性质尚未学好
评估方法
对于一个数据集,为兼顾训练与测试,从中产生训练集S与测试集T
留出法
即直接讲数据集拆分成两个互斥的集合。还有分层采样等方式,通常训练集占2/3-4/5
交叉验证法
自助法
其思想主要是:每次随机从 D 中挑选一个样本,将其拷贝放入 DF’ 然后再将该样本放回初始数据集 D 中,使得该样本在
下次采样时仍有可能被采到;这个过程重复执行 m 次后,我们就得到了包含m个样本的数据集DF。
lim m ↦ ∞ ( 1 − 1 m ) m ↦ 1 e ≈ 0.368 \lim _{m \mapsto \infty}\left(1-\frac{1}{m}\right)^m \mapsto \frac{1}{e} \approx 0.368 m↦∞lim(1−m1)m↦e1≈0.368
调参
验证集(validation set)参与调参,测试集不参与
性能度量
通过对比预测结果与真实结果,计算两者的误差。
均方误差:
E ( f ; D ) = 1 m ∑ i = 1 m ( f ( x i ) − y i ) 2 E(f ; D)=\frac{1}{m} \sum_{i=1}^m\left(f\left(\boldsymbol{x}_i\right)-y_i\right)^2 E(f;D)=m1i=1∑m(f(xi)−yi)2
对于数据分布D和概率密度函数 p ( x ) p(x) p(x)其也可写成:
E ( f ; D ) = ∫ x ∼ D ( f ( x ) − y ) 2 p ( x ) d x E(f ; \mathcal{D})=\int_{\boldsymbol{x} \sim \mathcal{D}}(f(\boldsymbol{x})-y)^2 p(\boldsymbol{x}) \mathrm{d} \boldsymbol{x} E(f;D)=∫x∼D(f(x)−y)2p(x)dx
错误率与精度
错误率定义为:
E ( f ; D ) = 1 m ∑ i = 1 m I ( f ( x i ) ≠ y i ) E(f ; D)=\frac{1}{m} \sum_{i=1}^m \mathbb{I}\left(f\left(\boldsymbol{x}_i\right) \neq y_i\right) E(f;D)=m1i=1∑mI(f(xi)=yi)
特别的,符号 I \mathbb{I} I为指示函数,或示性函数(indicator function)。数学中,指示函数是定义在某集合X上的函数,表示其中有哪些元素属于某一子集A。
简而言之,括号为真则为1.
精度则定义为:
acc ( f ; D ) = 1 m ∑ i = 1 m I ( f ( x i ) = y i ) = 1 − E ( f ; D ) \begin{aligned} \operatorname{acc}(f ; D) &=\frac{1}{m} \sum_{i=1}^m \mathbb{I}\left(f\left(\boldsymbol{x}_i\right)=y_i\right) \\ &=1-E(f ; D) \end{aligned} acc(f;D)=m1i=1∑mI(f(xi)=yi)=1−E(f;D)
对于数据分布D和概率密度函数 p ( x ) p(x) p(x),两者可分别描述为:
E ( f ; D ) = ∫ x ∼ D I ( f ( x ) ≠ y ) p ( x ) d x E(f ; \mathcal{D})=\int_{\boldsymbol{x} \sim \mathcal{D}} \mathbb{I}(f(\boldsymbol{x}) \neq y) p(\boldsymbol{x}) \mathrm{d} \boldsymbol{x} E(f;D)=∫x∼DI(f(x)=y)p(x)dx
acc ( f ; D ) = ∫ x ∼ D I ( f ( x ) = y ) p ( x ) d x = 1 − E ( f ; D ) . \begin{aligned} \operatorname{acc}(f ; \mathcal{D}) &=\int_{\boldsymbol{x} \sim \mathcal{D}} \mathbb{I}(f(\boldsymbol{x})=y) p(\boldsymbol{x}) \mathrm{d} \boldsymbol{x} \\ &=1-E(f ; \mathcal{D}) . \end{aligned} acc(f;D)=∫x∼DI(f(x)=y)p(x)dx=1−E(f;D).
混淆矩阵(Confusion Matrix)
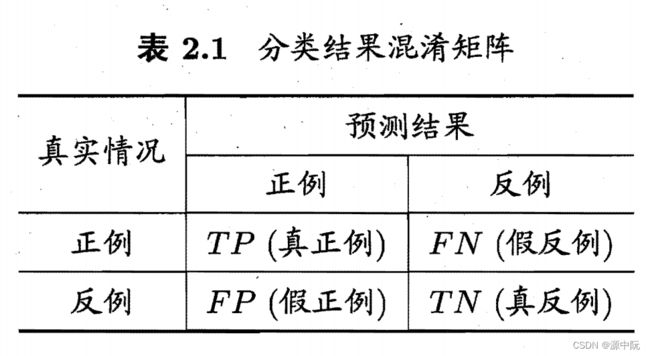
查准率 P 与查全率 R 分别定义为
P = T P T P + F P R = T P T P + F N \begin{aligned} &P=\frac{T P}{T P+F P} \\ &R=\frac{T P}{T P+F N} \end{aligned} P=TP+FPTPR=TP+FNTP
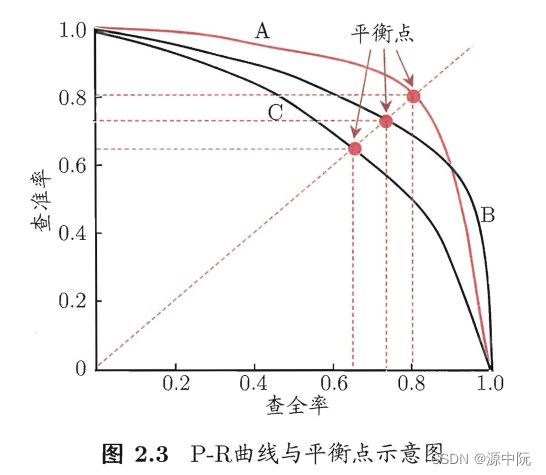
查准率和查全率是一对矛盾的度量.以查准率为纵轴、查全率为横轴作图 ,就得到了查准率-查全率曲线,简称 " P-R曲线"
常用F1度量(Fl 是基于查准率与查全率的调和平均 (harinonicmean)定义的)
F 1 = 2 × P × R P + R = 2 × T P 样例总数 + T P − T N F 1=\frac{2 \times P \times R}{P+R}=\frac{2 \times T P}{\text { 样例总数 }+T P-T N} F1=P+R2×P×R= 样例总数 +TP−TN2×TP
当对查准率与查全率重视程度不同时(如希望不能漏掉真例,或希望推荐内容用户的却感兴趣,减少打扰),定义 F β F_{\beta} Fβ如下
F β = ( 1 + β 2 ) × P × R ( β 2 × P ) + R F_\beta=\frac{\left(1+\beta^2\right) \times P \times R}{\left(\beta^2 \times P\right)+R} Fβ=(β2×P)+R(1+β2)×P×R
其中 β > 0 \beta > 0 β>0度量了查全率对查准率的相对重要性 [Van Rijsbergen, 1979]. β = 1 \beta = 1 β=1时退化为标准的 F1; β > 1 \beta > 1 β>1时查全率有更大影响 ; β < 1 \beta <1 β<1时查准率有更大影响。
ROC与SUC
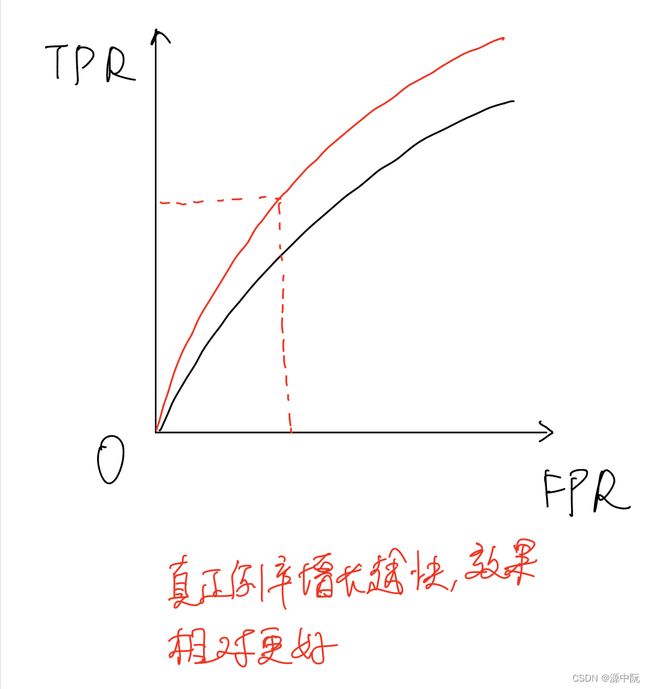
ROC 全称是"受试者工作特征" (Receiver Operating Characteristic) 曲线 ,
ROC 曲线的纵轴是"真正例率" (True Positive Rate,简称 TPR),横轴是"假正例率" (False PositiveRate,简称 FPR)

根据TPR的定义可以看出,当TPR的增长率相比更快时,模型效果更好
这里为了理解AUC的定义,引用了南瓜书关于AUC的内容。
A U C = 1 2 ∑ i = 1 m − 1 ( x i + 1 − x i ) ⋅ ( y i + y i + 1 ) \mathrm{AUC}=\frac{1}{2} \sum_{\mathrm{i}=1}^{\mathrm{m}-1}\left(\mathrm{x}_{\mathrm{i}+1}-\mathrm{x}_{\mathrm{i}}\right) \cdot\left(\mathrm{y}_{\mathrm{i}}+\mathrm{y}_{\mathrm{i}+1}\right) AUC=21i=1∑m−1(xi+1−xi)⋅(yi+yi+1)
假设预测结果为:
( s 1 , 0.77 , + ) , ( s 2 , 0.62 , − ) , ( s 3 , 0.58 , + ) , ( s 4 , 0.47 , + ) , ( s 5 , 0.47 , − ) , ( s 6 , 0.33 , − ) , ( s 7 , 0.23 , + ) , ( s 8 , 0.15 , − ) \left(\mathrm{s}_1, 0.77,+\right),\left(\mathrm{s}_2, 0.62,-\right),\left(\mathrm{s}_3, 0.58,+\right),\left(\mathrm{s}_4, 0.47,+\right),\left(\mathrm{s}_5, 0.47,-\right),\left(\mathrm{s}_6, 0.33,-\right),\left(\mathrm{s}_7, 0.23,+\right),\left(\mathrm{s}_8, 0.15,-\right) (s1,0.77,+),(s2,0.62,−),(s3,0.58,+),(s4,0.47,+),(s5,0.47,−),(s6,0.33,−),(s7,0.23,+),(s8,0.15,−)
三步:
1.先排序,从高到低
2.把每个作为阈值,如果是真正例就上升,假正例就下降,如果阈值改变不影响就斜着划(如图中的4.7)
3.步长为 1 / m + 1/m^+ 1/m+
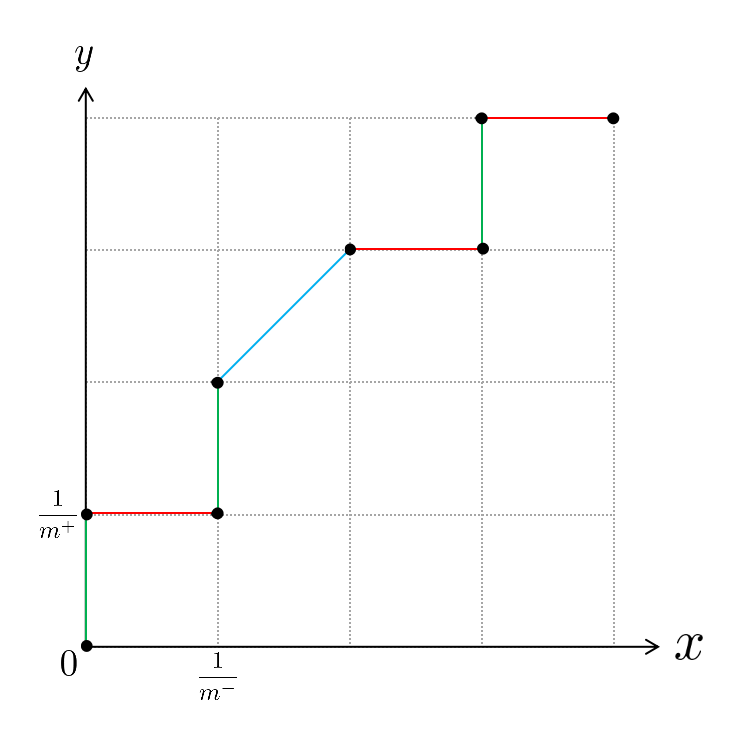
在这里我们为了能在解析公式(2.21)时复用此图所以没有写上具体地数值,转而用其数学符号代替。其中绿色线段表示在分类阈值变动的过程中只新增了真正例,红色线段表示只新增了假正例,蓝色线段表示既新增了真正例也新增了假正例。
根据\text{AUC}AUC值的定义可知,此时的\text{AUC}AUC值其实就是所有红色线段和蓝色线段与xx轴围成的面积之和。观察上图可知,红色线段与xx轴围成的图形恒为矩形,蓝色线段与xx轴围成的图形恒为梯形,但是由于梯形面积公式既能算梯形面积,也能算矩形面积,所以无论是红色线段还是蓝色线段,其与xx轴围成的面积都能用梯形公式来计算,也即
1 2 ⋅ ( x i + 1 − x i ) ⋅ ( y i + y i + 1 ) \frac{1}{2} \cdot\left(\mathrm{x}_{\mathrm{i}+1}-\mathrm{x}_{\mathrm{i}}\right) \cdot\left(\mathrm{y}_{\mathrm{i}}+\mathrm{y}_{\mathrm{i}+1}\right) 21⋅(xi+1−xi)⋅(yi+yi+1)
将其进行求和即可得到:
∑ i = 1 m − 1 [ 1 2 ⋅ ( x i + 1 − x i ) ⋅ ( y i + y i + 1 ) ] \sum_{i=1}^{m-1}\left[\frac{1}{2} \cdot\left(x_{i+1}-x_i\right) \cdot\left(y_i+y_{i+1}\right)\right] i=1∑m−1[21⋅(xi+1−xi)⋅(yi+yi+1)]
此即为AUC。为计算损失,其公式为
ℓ rank = 1 m + m − ∑ x + ∈ D + ∑ x − ∈ D − ( I ( f ( x + ) < f ( x − ) ) + 1 2 I ( f ( x + ) = f ( x − ) ) ) \ell_{\text {rank }}=\frac{1}{\mathrm{~m}^{+} \mathrm{m}^{-}} \sum_{x^{+} \in \mathrm{D}^{+}} \sum_{\boldsymbol{x}^{-} \in \mathrm{D}^{-}}\left(\mathbb{I}\left(\mathrm{f}\left(\boldsymbol{x}^{+}\right)<\mathrm{f}\left(\boldsymbol{x}^{-}\right)\right)+\frac{1}{2} \mathbb{I}\left(\mathrm{f}\left(\boldsymbol{x}^{+}\right)=\mathrm{f}\left(\boldsymbol{x}^{-}\right)\right)\right) ℓrank = m+m−1x+∈D+∑x−∈D−∑(I(f(x+)<f(x−))+21I(f(x+)=f(x−)))
对于rankloss的解释没有进一步研究,后期用到再看。
代价敏感错误率与代价敏感曲线
为权衡不同类型错误所造成的不同损失,可为错误赋予"非均等代价" (unequa1 cost)。

若将第 0 类判别为第 1 类所造成的损失更大,则 cost01 > cost l0; 损失程度相差越大 , cost01 与 cost l0 值的差别越大.
E ( f ; D ; cost ) = 1 m ( ∑ x i ∈ D + I ( f ( x i ) ≠ y i ) × cost 01 + ∑ x i ∈ D − I ( f ( x i ) ≠ y i ) × cost 10 ) \begin{aligned} E(f ; D ; \operatorname{cost})=& \frac{1}{m}\left(\sum_{\boldsymbol{x}_i \in D^{+}} \mathbb{I}\left(f\left(\boldsymbol{x}_i\right) \neq y_i\right) \times \operatorname{cost}_{01}\right.&\left.+\sum_{\boldsymbol{x}_i \in D^{-}} \mathbb{I}\left(f\left(\boldsymbol{x}_i\right) \neq y_i\right) \times \operatorname{cost}_{10}\right) \end{aligned} E(f;D;cost)=m1(xi∈D+∑I(f(xi)=yi)×cost01+xi∈D−∑I(f(xi)=yi)×cost10)
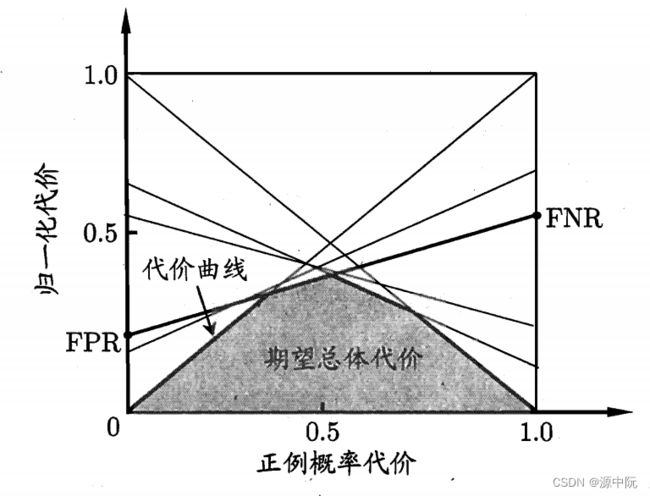
为了反应学习器期望总体代价,定义代价曲线(cost curve)。其横轴为取值为[0,1]的正例概率代价
P ( + ) cost = p × cost 01 p × cost 01 + ( 1 − p ) × cost 10 P(+) \operatorname{cost}=\frac{p \times \operatorname{cost}_{01}}{p \times \operatorname{cost}_{01}+(1-p) \times \operatorname{cost}_{10}} P(+)cost=p×cost01+(1−p)×cost10p×cost01
其中p是样例为正例的概率;纵轴是取值为[0,1]的归一化代价。
cost n o r m = FNR × p × cost 01 + F P R × ( 1 − p ) × cost 10 p × cost 01 + ( 1 − p ) × cost 10 \operatorname{cost}_{n o r m}=\frac{\text { FNR } \times p \times \operatorname{cost}_{01}+\mathrm{FPR} \times(1-p) \times \operatorname{cost}_{10}}{p \times \operatorname{cost}_{01}+(1-p) \times \operatorname{cost}_{10}} costnorm=p×cost01+(1−p)×cost10 FNR ×p×cost01+FPR×(1−p)×cost10
比较检验
统计假设检验 (hypothesis test)为我们进行学习器性能比较提供了重要依据。基于假设检验结果我们可推断出,若在测试集上观察到学习器 A 比 B 好,则 A 的泛化性能是否在统计意义上优于 B,以及这个结论的把握有多大。
问题:
1.测试集上到性能与真正的泛化性能未必相同
2.测试集不同反应出来的性能不同
3.机器学习算法本身具有一定的随机性,同一个测试集运行多次,结果可能不一样。
因此,需要引入假设检验的方法,检验模型的泛化性能。
假设检验
复习概率论!!!!
二项分布
P ( ϵ ^ ; ϵ ) = ( m ϵ ^ × m ) ϵ ϵ ^ × m ( 1 − ϵ ) m − ϵ ^ × m P(\hat{\epsilon} ; \epsilon)=\left(\begin{array}{c} m \\ \hat{\epsilon} \times m \end{array}\right) \epsilon^{\hat{\epsilon} \times m}(1-\epsilon)^{m-\hat{\epsilon} \times m} P(ϵ^;ϵ)=(mϵ^×m)ϵϵ^×m(1−ϵ)m−ϵ^×m
个人理解,这个公式可以看作
P = C m n q n ( 1 − q ) m − n P = C_{m}^{n} q^{n}(1-q)^{m-n} P=Cmnqn(1−q)m−n
