通俗易懂的RNN

一、什么是RNN

RNN（Recurrent Neural Network）是一类用于处理序列数据的神经网络。首先我们要明确什么是序列数据，摘取百度百科词条：时间序列数据是指在不同时间点上收集到的数据，这类数据反映了某一事物、现象等随时间的变化状态或程度。这是时间序列数据的定义，当然这里也可以不是时间，比如文字序列，但总归序列数据有一个特点——后面的数据跟前面的数据有关系。

RNN是神经网络的一种，类似的还有深度神经网络DNN，卷积神经网络CNN，生成对抗网络GAN，等等。RNN对具有序列特性的数据非常有效，它能挖掘数据中的时序信息以及语义信息，利用了RNN的这种能力，使深度学习模型在解决语音识别、语言模型、机器翻译以及时序分析等NLP领域的问题时有所突破。

举几个具有序列特性的例子：

• 拿人类的某句话来说，也就是人类的自然语言，是不是符合某个逻辑或规则的字词拼凑排列起来的，这就是符合序列特性。
• 语音，我们发出的声音，每一帧每一帧的衔接起来，才凑成了我们听到的话，这也具有序列特性。
• 股票，随着时间的推移，会产生具有顺序的一系列数字，这些数字也是具有序列特性。

二、为什么要发明RNN

我们先来看一个NLP很常见的问题，命名实体识别，举个例子，现在有两句话：

第一句话：I like eating apple！（我喜欢吃苹果！）

第二句话：The Apple is a great company！（苹果真是一家很棒的公司！）

现在的任务是要给apple打Label，我们都知道第一个apple是一种水果，第二个apple是苹果公司，假设我们现在有大量的已经标记好的数据以供训练模型，当我们使用全连接的神经网络时，我们做法是把apple这个单词的特征向量输入到我们的模型中（如下图），在输出结果时，让我们的label里，正确的label概率最大，来训练模型，但我们的语料库中，有的apple的label是水果，有的label是公司，这将导致，模型在训练的过程中，预测的准确程度，取决于训练集中哪个label多一些，这样的模型对于我们来说完全没有作用。问题就出在了我们没有结合上下文去训练模型，而是单独的在训练apple这个单词的label，这也是全连接神经网络模型所不能做到的，于是就有了我们的循环神经网络。

【全连接神经网络结构】

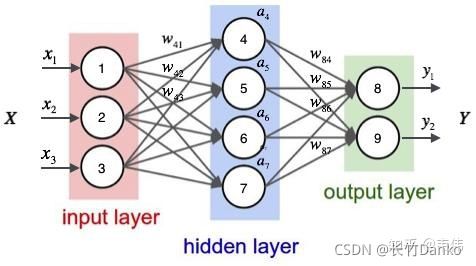
三、RNN的基础知识

1、循环核介绍

循环核具有记忆力，通过不同时刻的参数共享，实现了对时间序列的信息提取

• ht：记忆体内当前时刻存储的状态信息
• xt：当前时刻输入特征
• ht-1：记忆体上一时刻存储的状态信息
• yt：当前时刻循环核的输出特征

2、循环核按时间步展开

按时间步展开，就是把循环核按照时间轴方向展开。每个时刻记忆体状态信息ht被刷新，记忆体周围的参数矩阵wxh、whh和why是固定不变的。要训练优化的就是这些参数矩阵。训练完成后，使用效果最好的参数矩阵，执行前向传播，输出预测结果。循环神经网络，就是借助循环核提取时间特征后，送入全连接网络，实现连续数据的预测。

3、记忆体

循环核按照时间步展开后，可以发现，循环核是由多个记忆体构成，记忆体是循环神经网络储存历史状态信息的载体，每个记忆体都可以设定相应的个数，这个个数决定了记忆体可以存储历史状态信息的能力，记忆体个数越多，训练效果越好，但是由于记忆体的个数决定了参数矩阵的维度，因此记忆体个数越多，需要训练的参数量就越多，所需要消耗的资源就越大，训练时间就越长，因此需酌情评估。图中的例子中记忆体的个数为3，这个记忆体的个数，决定了ht的维度，进一步决定了Wxh、Whh以及Why的维度。

对于记忆体，还有一种更好的理解方式，输入xt+记忆体ht+输出yt这一个结构其实对应的就是全连接神经网络，其中输入层就是输入xt，隐藏层就是记忆体，隐藏层神经元的个数即是记忆体的个数，输出层就是输出yt，具体图示如下：

图中的Wxh维度是3x4，Whh维度是4x4，Why维度是4x2。

4、循环计算层

每个循环核构成一层循环计算层。循环计算层的层数时是向输出方向增长的。

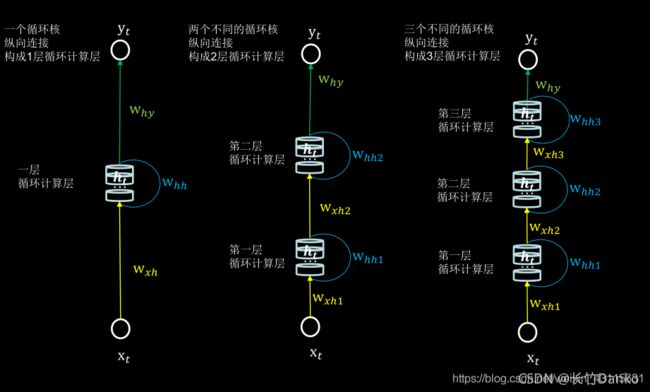
5、TF描述循环计算层

tf.keras.layers.SimpleRNN(记忆体个数,
                          activation = '激活函数',  # 其中默认为tanh
                          return_sequences = Ture or False  # 是否每个时刻输出ht到下一层，
                                                            # 如果不是则仅最后时间步输出ht，False为默认值
                          
)

（1）每个时间步都会输出ht：一般是中间层

（2）仅最后时间步输出ht：一般是输出层

二、RNN的补充知识

1、RNN梯度消失的原因

RNN和DNN梯度消失的原因是不同的，DNN梯度消失及梯度爆炸的原因可见之前的文章，这里我们介绍RNN梯度消失的原因。

RNN结构如图：

【注】：图中的隐藏层标记St与上面图片中的标识ht不同，标识只是用于推导RNN梯度消失的原因，无其他含义。

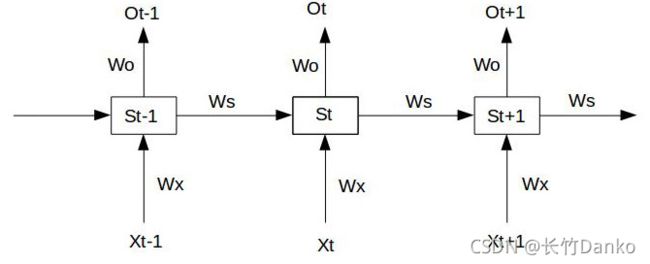
假设我们的时间序列只有三段， [公式] 为给定值，神经元没有激活函数，则RNN最简单的前向传播过程如下：

$S_1=W_x{X}_1+W_s{S}_0+b_1$
$O_1=W_o{S}_1+b_2$
$S_2=W_x{X}_2+W_s{S}_1+b_1$
$O_2=W_o{S}_2+b_2$
$S_3=W_x{X}_3+W_s{S}_2+b_1$
$O_3=W_o{S}_3+b_2$

输入时间序列长度为t的数据，假设在t时刻，损失函数为$L_t=\frac{1}{2}(Y_t-O_t{)}^2$。

使用随机梯度下降算法训练RNN，其实就是对$W_x、W_s、W_o$以及$b_1、b_2$求偏导，并不断调整它们，使得$L_t$尽可能小的过程。
现在假设我们的时间序列只有3段，$t_1、t_2、t_3$。

我们对$t_3$时刻的$W_x、W_s、W_o$求偏导（其他时刻类似）：

$\frac{\partial L_3}{\partial W_0}=\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial W_o}$

$\frac{\partial L_3}{\partial W_x}=\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial S_3}\frac{\partial S_3}{\partial W_x}+\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial S_3}\frac{\partial S_3}{\partial S_2}\frac{\partial S_2}{\partial W_x}+\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial S_3}\frac{\partial S_3}{\partial S_2}\frac{\partial S_2}{\partial S_1}\frac{\partial S_1}{\partial W_x}$

$\frac{\partial L_3}{\partial W_s}=\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial S_3}\frac{\partial S_3}{\partial W_s}+\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial S_3}\frac{\partial S_3}{\partial S_2}\frac{\partial S_2}{\partial W_s}+\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial S_3}\frac{\partial S_3}{\partial S_2}\frac{\partial S_2}{\partial S_1}\frac{\partial S_1}{\partial W_s}$

可以看出对于$W_0$求偏导并没有长期依赖，但是对于$W_x、W_s$求偏导，会随着时间序列产生长期依赖。因为$S_t$随着时间序列向前传播，而$S_t$又是$W_x、W_s$的函数。

根据上述求偏导的过程，我们可以得出任意时刻对$W_x、W_s$求偏导的公式：

$\frac{\partial L_t}{\partial W_x}={\sum }_{k=0}^t\frac{\partial L_t}{\partial O_t}\frac{\partial O_t}{\partial S_t}({\prod }_{j=k+1}^t\frac{\partial S_j}{\partial S_{j-1}})\frac{\partial S_k}{\partial W_x}$

$\frac{\partial L_t}{\partial W_s}={\sum }_{k=0}^t\frac{\partial L_t}{\partial O_t}\frac{\partial O_t}{\partial S_t}({\prod }_{j=k+1}^t\frac{\partial S_j}{\partial S_{j-1}})\frac{\partial S_k}{\partial W_s}$

如果加上激活函数，$S_j=tanh(W_x{X}_j+W_s{S}_{j-1}+b_1)$，

则${\prod }_{j=k+1}^t\frac{\partial S_j}{\partial S_{j-1}}={\prod }_{j=k+1}^{t}tan{h}^{{}^{\prime }}{W}_s$

由于激活函数tanh的导数是小于1的，因此随着累乘的增加，RNN会出现梯度消失的情况。

现在来解释一下，为什么说RNN和DNN的梯度消失问题含义不一样？

1. 先来说DNN中的反向传播：在DNN梯度消失及梯度爆炸的文章中，我推导了两个权重的梯度，第一个梯度是直接连接着输出层的梯度，求解起来并没有梯度消失或爆炸的问题，因为它没有连乘，只需要计算一步。第二个梯度出现了连乘，也就是说越靠近输入层的权重，梯度消失或爆炸的问题越严重，可能就会消失会爆炸。一句话总结一下，DNN中各个权重的梯度是独立的，该消失的就会消失，不会消失的就不会消失。
2. 再来说RNN：RNN的特殊性在于，它的权重是共享的。抛开$W_o$不谈，因为它在某时刻的梯度不会出现问题（某时刻并不依赖于前面的时刻），但是$W_s$和$W_x$就不一样了，每一时刻都由前面所有时刻共同决定，是一个相加的过程，这样的话就有个问题，当距离长了，计算最前面的导数时，最前面的导数就会消失或爆炸，但当前时刻整体的梯度并不会消失，因为它是求和的过程，当下的梯度总会在，只是前面的梯度没了，但是更新时，由于权值共享，所以整体的梯度还是会更新，通常人们所说的梯度消失就是指的这个，指的是当下梯度更新时，用不到前面的信息了，因为距离长了，前面的梯度就会消失，也就是没有前面的信息了，但要知道，整体的梯度并不会消失因为当下的梯度还在，并没有消失。
3. 一句话概括：RNN的梯度不会消失，RNN的梯度消失指的是当下梯度用不到前面的梯度了，但DNN靠近输入的权重的梯度是真的会消失，RNN 所谓梯度消失的真正含义是，梯度被近距离梯度主导，导致模型难以学到远距离的依赖关系。

【注】RNN实战可参考B站技术视频：北京大学-Tensorflow2.0-曹健老师