RNN详解

回顾FNN

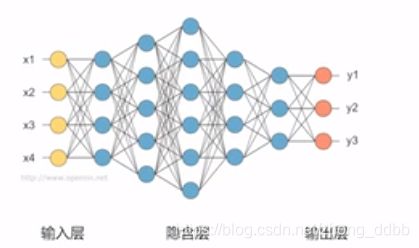
先来回顾一下前馈神经网络（FNN），网络结构如下图所示：

对于每个神经元进行如下运算：

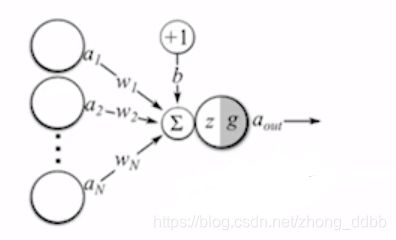
先进行加权求和
$$z=b+\sum _{i=1}^N{w}_i{x}_i$$
在进行非线性变换：
$$\begin{gathered} g(x)=\sigma (x)=\frac{1}{1+e^{-x}} \\ {a}_{out}=g(z)=\sigma (\sum _{i=1}^N{w}_i{x}_i+b) \end{gathered}$$
所以，整个神经网络相当于一个复合函数。

RNN基本模型

基本结构

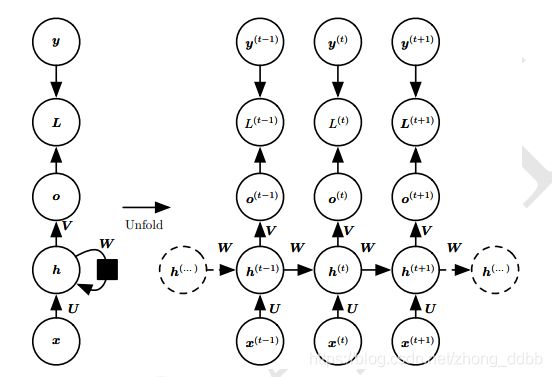
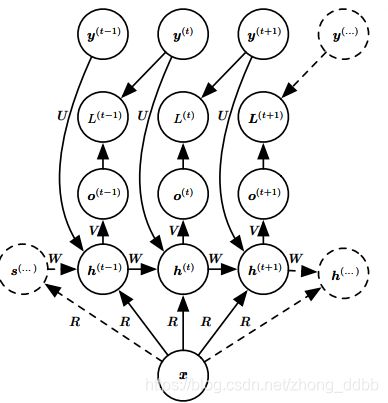
循环神经网络的结构如下：

将输入序列$x$映射到输出值$o$的对应序列。损失$L$衡量每个输出$o$与相应的训练目标$y$的距离。

输入到隐藏的连接由权重矩阵为$U$，隐藏到隐藏的循环连接由权重矩阵为$W$，隐藏到输出的连接由权重矩阵为$V$。RNN是共用一组参数。

该模型中的前向传播定义如下：
$$\begin{array}{rl}& {\mathbf{a}}^{(t)}=\mathbf{b}+\mathbf{W}{\mathbf{h}}^{(t-1)}+\mathbf{U}{\mathbf{x}}^{(t)}\\ & {\mathbf{h}}^{(t)}=\tanh ({\mathbf{a}}^{(t)})\\ & {\mathbf{o}}^{(t)}=\mathbf{c}+\mathbf{V}{\mathbf{h}}^{(t)}\\ & {\hat{\mathbf{y}}}^{(t)}=softmax({\mathbf{o}}^{(t)})\end{array}$$

这个循环网络将一个输入序列映射到相同长度的输出序列。与$x$序列配对的$y$的总损失是所有时间步的损失之和。采用极大似然函数的负数作为损失函数：
$$\begin{array}{rl}& L(\{x^{(1)},\dots ,x^{(\tau )}\},\{y^{(1)},\dots ,y^{(\tau )}\})\\ & =\sum _t{L}^{(t)}\\ & =-\sum _t\log P_{model}(y^{(t)}|\{x^{(1)},\dots ,x^{(\tau )}\})\end{array}$$
接下来通过时间反向传播（back-propagation through time，BPTT）来更新网络参数。

每一次梯度计算涉及执行一次前向传播，接着是由右到左的反向传播。运行时
间是 $O(\tau )$，并且不能通过并行化来降低，因为前向传播图是固有循序的; 每个时间
步只能一前一后地计算。前向传播中的各个状态必须保存，直到它们反向传播中被
再次使用，因此内存代价也是 $O(\tau )$。

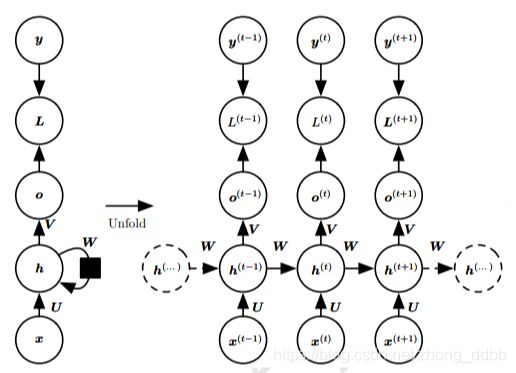
通过时间反向传播

循环神经网络的参数包括$\mathbf{U},\mathbf{V},\mathbf{W},\mathbf{b},\mathbf{c}$，对于每一个节点N，需要基于N后面的节点的梯度，递归进行计算。

从最终的损失的节点开始递归：
$$\frac{\partial L}{\partial L^{(t)}}=1$$

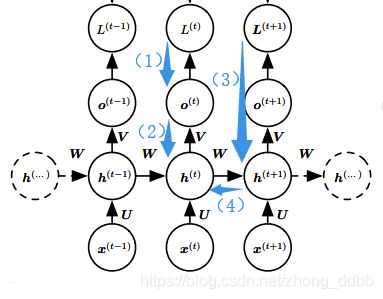
如下图所示：

可知通过时间反向传播梯度，注意${\mathbf{h}}^{(t)}$ 同时具有${\mathbf{o}}^{(t)}$ 和${\mathbf{h}}^{(t+1)}$ 后续两个节点，所以$L$对${\mathbf{h}}^{(t)}$的求导包括两个部分$L^{(t)}$对${\mathbf{h}}^{(t)}$的求导和$L^{(t+1)}$对${\mathbf{h}}^{(t)}$的求导。

（1）损失函数$L$关于时间步 $t$ 的输出 ${\mathbf{o}}^{(t)}$ d的梯度，先给出求导结果：
$$({\nabla }_{{\mathbf{o}}^{(t)}}L{)}_i=\frac{\partial L}{\partial o_i^{(t)}}=\frac{\partial L}{\partial L^{(t)}}\frac{\partial L^{(t)}}{\partial o_i^{(t)}}={\hat{y}}_i^{(t)}-1_{i,y^{(t)}}=\{\begin{array}{l}{\hat{y}}_i^{(t)}-1\\ {\hat{y}}_i^{(t)}-0\end{array}$$
上式可以理解为：期望输出的概率—该位置对应的真实label，$1_{i,y^{(t)}}$表示label，有两种取值0或1。

这个求导过程比较复杂，可以参考softmax回归详解，文中详细推导了以下结论：

若：
$$\begin{gathered} s_i=\frac{e^{z_i}}{{\sum }_{j=1}^K{e}^{z_i}}i=1,2,\dots ,K \\ L(w)=-\log P(y^{(i)}|x^{(i)};w) \end{gathered}$$
则：
$$\frac{\partial \mathrm{L}}{\partial {\mathrm{z}}_i}=s_i-y_i$$
其中:

$s_i$ 为经过softmax的结果，可以理解为概率，对应RNN中的${\hat{y}}_i^{(t)}$。

$y_i=1或y_i=0$，对应RNN中的$1_{i,y^{(t)}}$。

$z_i$对应RNN的输出${\mathbf{o}}^{(t)}$。

（2）所以$L$ 对${\mathbf{h}}^{(\tau )}$ 求导
$${\nabla }_{{\mathbf{h}}^{(\tau )}}L={\mathbf{V}}^T{\nabla }_{{\mathbf{o}}^{(\tau )}}L$$
（3）最终的梯度下降包括两个部分。
$$\begin{array}{l}{\nabla }_{h^{(t)}}L={\left(\frac{\partial {\mathbf{h}}^{(t+1)}}{\partial {\mathbf{h}}^{(t)}}\right)}^{\top }\left({\nabla }_{{\mathbf{h}}^{(t+1)}}L\right)+{\left(\frac{\partial {\mathbf{o}}^{(t)}}{\partial {\mathbf{h}}^{(t)}}\right)}^{\top }\left({\nabla }_{{\mathbf{o}}^{(t)}}L\right)\\ ={\mathbf{W}}^{\top }\left({\nabla }_{{\mathbf{h}}^{(t+1)}}L\right)\mathrm{diag}\left(1-{\left({\mathbf{h}}^{(t+1)}\right)}^2\right)+{\mathbf{V}}^{\top }\left({\nabla }_{{\mathbf{o}}^{(t)}}L\right)\end{array}$$
其中：
$$\begin{array}{rl}\frac{\partial {\mathbf{h}}^{(t+1)}}{\partial {\mathbf{h}}^{(t)}}& =\frac{\partial \tanh (\mathbf{b}+\mathbf{W}{\mathbf{h}}^{(t)}+\mathbf{U}{\mathbf{x}}^{(t+1)})}{\partial {\mathbf{h}}^{(t)}}\\ & ={\mathbf{W}}^{T}diag(1-({\mathbf{h}}^{(t+1)}{)}^2)\end{array}$$
注：${\tanh }^{\prime }(x)=1-(tanh(x){)}^2$

$diag(1-({\mathbf{h}}^{(t+1)}{)}^2)$ 是包含元素$1-(h_i^{(t+1)}{)}^2$的对角矩阵。

（4）更新参数

通过前面的步骤，可以得到以下参数梯度：
$$\begin{array}{rl}{\nabla }_{c}L& =\sum _t{\left(\frac{\partial {\mathbf{o}}^{(t)}}{\partial \mathbf{c}}\right)}^{\top }{\nabla }_{{\mathbf{o}}^{(t)}}L=\sum _t{\nabla }_{{\mathbf{o}}^{(t)}}L\\ {\nabla }_{\mathbf{b}}L& =\sum _t{\left(\frac{\partial {\mathbf{h}}^{(t)}}{\partial {\mathbf{b}}^{(t)}}\right)}^{\top }{\nabla }_{{\mathbf{h}}^{(t)}}L=\sum _t\mathrm{diag}\left(1-{\left({\mathbf{h}}^{(t)}\right)}^2\right){\nabla }_{{\mathbf{h}}^{(t)}}L\\ {\nabla }_{\mathbf{V}}L& =\sum _t\sum _i\left(\frac{\partial L}{\partial o_i^{(t)}}\right){\nabla }_{\mathbf{V}}{o}_i^{(t)}=\sum _t\left({\nabla }_{o^{(t)}}L\right){\mathbf{h}}^{(t{)}^{\top }}\\ {\nabla }_{\mathbf{W}}& =\sum _t\sum _i\left(\frac{\partial L}{\partial h_i^{(t)}}\right){\nabla }_{{\mathbf{W}}^{(t)}}{h}_i^{(t)}\\ & =\sum _t\mathrm{diag}\left(1-{\left({\mathbf{h}}^{(t)}\right)}^2\right)\left({\nabla }_{{\mathbf{h}}^{(t)}}L\right){\mathbf{h}}^{(t-1{)}^{\top }}\\ {\nabla }_{U}L& =\sum _t\sum _i\left(\frac{\partial L}{\partial h_i^{(t)}}\right){\nabla }_{{\mathbf{U}}^{(t)}}{h}_i^{(t)}\\ & =\sum _t\mathrm{diag}\left(1-{\left({\mathbf{h}}^{(t)}\right)}^2\right)\left({\nabla }_{{\mathbf{h}}^{(t)}}L\right){\mathbf{x}}^{(t{)}^{\top }}\end{array}$$

几种特殊RNN

基于上下文的RNN

将向量序列$\mathbf{X}=({\mathbf{x}}^{(1)},\dots ,{\mathbf{x}}^{(n_x)})$ 作为输入，而不是仅接收单个向量$\mathbf{x}$ 作为输入。这类RNN适用于很多任务如图注，其中单个图像作为模型的输入，然后产生描述图像的词序列。观察到的输出序列的每个元素 $y^{(t)}$ 同时用作输入（对于当前时间步）和训练期间的目标（对于前一时间步）。

此RNN包含从前一个输出到当前状态的连接。

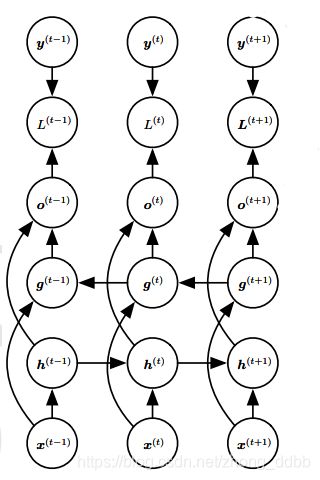
双向RNN

双向RNN是指结合时间上从序列起点开始移动的RNN和另一个时间上从序列末尾开始移动的RNN，典型的双向RNN如下图所示：

其中 ${\mathbf{h}}^{(t)}$代表通过时间向前移动的子RNN的状态，${\mathbf{g}}^{(t)}$代表通过时间向后移动的子RNN的状态，此时，输出单元${\mathbf{o}}^{(t)}$ 可以受益于输入${\mathbf{h}}^{(t)}$ 关于过去的相关信息以及输入${\mathbf{g}}^{(t)}$ 中关于未来的相关信息。

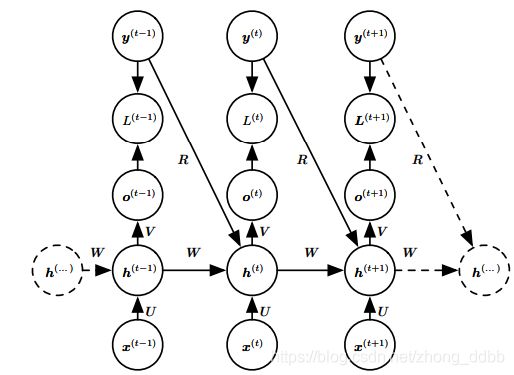
基于编码—解码的序列到序列架构

这种RNN最大的特点是输入序列和输出序列不一定等长。

主要想法是：

（1）编码器RNN处理输入序列，编码器输出上下文C，这个C是一个概况输入序列$\mathbf{X}=({\mathbf{x}}^{(1)},\dots ,{\mathbf{x}}^{(n_x)})$ 的向量或向量序列。

（2）解码器RNN则以固定长度向量为条件产生输出序列$\mathbf{Y}=({\mathbf{y}}^{(1)},\dots ,{\mathbf{y}}^{(n_y)})$。

（3）两个RNN共同训练以最大化$\log P({\mathbf{y}}^{(1)},\dots ,{\mathbf{y}}^{(n_y)}|{\mathbf{x}}^{(1)},\dots ,{\mathbf{x}}^{(n_x)})$

主要应用有语音识别，机器翻译和问答系统。

RNN缺陷：无法做到长期依赖

权值$W$角度

回顾RNN模型

循环联系：
$${\mathbf{h}}^{(t)}={\mathbf{W}}^T{\mathbf{h}}^{(t-1)}$$
可以简化为：
$${\mathbf{h}}^{(t)}=({\mathbf{W}}^t{)}^T{\mathbf{h}}^{(0)}$$

当$\mathbf{W}$ 符合下列形式的特征分解：
$$\mathbf{W}=\mathbf{Q}\mathbf{\Sigma }{\mathbf{Q}}^T$$
其中$\mathbf{Q}$是正交矩阵。

所以：
$${\mathbf{h}}^{(t)}={\mathbf{Q}}^T{\mathbf{\Sigma }}^t\mathbf{Q}{\mathbf{h}}^{(0)}$$
对于${\mathbf{\Sigma }}^t$ ，经过$t$次相乘后，即：经过多个阶段的传播后：如果特征值小于1，特征值将衰减到零。如果特征值大于1，经过$t$次相乘后，特征值将激增。任何不与最大特征向量对齐的${\mathbf{h}}^{(0)}$的部分将最终被丢弃，无法做到长期依赖。

梯度消失/爆炸角度

如下图所示：

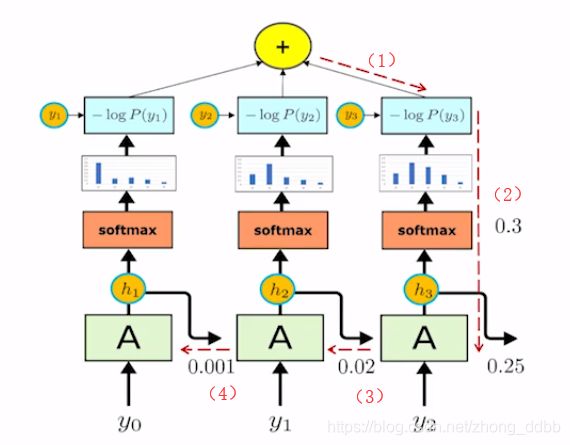
如上图(1)-(4)的反向传播过程：
$$\frac{\partial J}{\partial y_0}=\frac{\partial J}{\partial h_3}\frac{\partial h_3}{\partial h_2}\frac{\partial h_2}{\partial h_1}\frac{\partial h_1}{\partial y_0}$$
如果这个过程中：

（1）这一连串偏导数都小于1，这些小数连乘，可能会导致最终的结果趋于0，甚至等于0，造成梯度消失。梯度消失意味着无法通过加深网络层数来提升预测效果，只有靠近输出的几层才真正起到学习的作用，这样RNN很难学习到输入序列中的长距离依赖关系。

（2）这一连串偏导数都大于1，这些数连乘，可能会导致最终的结果趋于无穷大，造成梯度爆炸。以通过梯度裁剪来缓解，即当梯度的范式大于某个给定值的时候，对梯度进行等比缩放。

为了解决以上两个问题，我们引入LSTM。

RNN应用

RNN通常用于处理离散序列数据（离散线性，长度可变）；

从RNN结构来理解其应用：

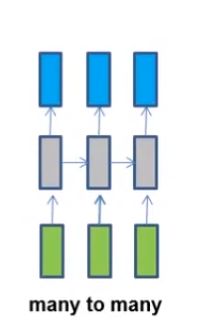
（1）词性标注，输入是每个词对应的向量，输出是词对应的词性。网络结构如下：

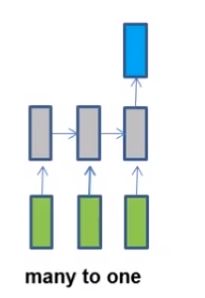
（2）情感分析，输入一句话，输出其情感的倾向标签。网络结构如下：

（3）机器翻译，输入是一种语言，输出是另一种语言。网络结构如下：

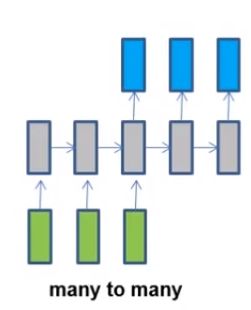
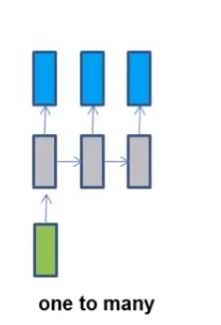
（4）图片文字生成，输入是一张图片，生成图片的描述。网络结构如下：

从功能的角度理解RNN应用：

（1）序列数据的分析，如市场趋势预测。

（2）序列数据的生成，如基于图片的诗歌创作。

（3）序列数据的转换，如语音识别，机器翻译。