数字图像处理练习题整理 (一)

• 注: 内容仅供参考, 不保证正确性, 如有误欢迎交流指正.
• 鸣谢: 感谢 小组的各位同学为内容整理提供的帮助

说明：不要直接使用MATLAB（或者OPENCV、PYTHON等）所带的图像处理函数，重点考察大家是否理解了各种处理算法。读写图像、显示图像等可直接使用库函数。若自己编程实现了某功能，则应与直接调用库函数的方法进行对比，看结果是否一致，运行速度如何。

一. 图像的获取

什么是图像的空间分辨率?
直观上看，空间分辨率是图像中可辨别的最小细节的度量。在数量上，空间分辨率可以有很多方法来说明，其中每单位距离线对数和每单位距离点数(像素数)是最通用的度量。空间分辨率度量用每英寸点数（DPI）来表示。空间分辨率越大，图片效果越好。

什么是密度（灰度）分辨率？
灰度分辨率是指在灰度级中可分辨的最小变化。灰度分辨率指的是色阶，色阶是表示图像亮度强弱的指数标准，也就是我们说的色彩指数。灰度分辨率指亮度，和颜色无关，但最亮的只有白色，最不亮的只有黑色。灰度分辨率表示：常用2的整数次幂，最常用是2的8次方=256。

在图像取样和量化中，DPI （Dots Per Inch）或者PPI（pixels per inch）与空间分辨率有何关系？
DPI(dots per inch)：打印分辨率（每英寸所能打印的点数，即打印精度）
PPI(pixels per inch)：图像的采样率（在图像中，每英寸所包含的像素数目）

空间分辨率与图像采样相结合，采样对应空间分辨率.
灰度分辨率与图像量化相结合，量化对应灰度分辨率.
对坐标值进行数字化称为取样，对幅值数字化称为量化。

对一幅图像，当量化级数一定时，采样点数对图像质量有着显著的影响。采样点数越多，图像质量越好； 当采样点数减少时，图上的块状效应就逐渐明显。
同理，当图像的采样点数一定时，采用不同量化级数的图像质量也不一样。量化级数越多，图像质量越好，当量化级数越少时，图像质量越差，量化级数最小的极端情况就是二值图像，图像出现假轮廓.

二. 图像的几何变换

1. 图像放大缩小

设一幅大小为M×N的灰度图像I中，现要变成（放大或缩小）为 P×Q的图像J，请写出J的生成算法。【参考函数：imresize】

算法的具体步骤如下: 假设原图像大小为 $M\ast N$, 其中 $M$ 和 $N$ 分别为原始图像的行数与列数。若图像的缩放因子为 $t(t>0)$, 则目标图像大小 $size=t\ast m\ast t\ast n$。对于目标图像的某个像素点 $P(x,y)$, 通过 $P\ast 1/t$ 可以得到对应的原始图像坐标 $P^{\prime }(x_1,y_1)$, 其中 $x_1=x/t,y_1=y/t$, 考虑到 $x_1,y_1$ 都不是整数而不存在这样的点, 因此可以找出与它相临的四个点的灰度 $f_1,f_2,f_3,f_4$, 使用双线性插值算法便得到了该像素点 $P^{\prime }(x_1,y_1)$ 的灰度, 也即像素 $P(x,y)$ 的灰度.
完整算法描述如下:

1. 通过原始图像和比例因子得到新图像的大小并创建新图像
2. 由新图像的某个像素 $(x,y)$ 映射到原始图像 $(x^{\prime },y^{\prime })$ 处
3. 对 $x^{\prime },y^{\prime }$ 向下取整得到 $([x],[y]),([x]+1,[y]),([x]，[y]+1),([x]+1,[y]+1)$ 的值
4. 利用双线性插值公式计算公式得到像素点 $(x,y)$ 的值并写回新图像
5. 重复步骤 (2) 直到新图像的所有像素写完
   注:

• 需要在原图像矩阵的最后加上一行和一列的 0, 以避免索引原图像矩阵时的边界溢出问题.
• 对于彩色图像需要将 R, G, B 三个颜色通道分离出来单独计算; 计算完成后再合并组装成彩色图像
• 双线性插值计算公式：(其中, $i,j$ 为浮点坐标整数部分; $u,v$ 为浮点坐标小数部分. 即 $(x^{\prime },y^{\prime })==(i+u,j+v)$)
  $$f(i+u,j+v)=(1-u)(1-v)f(i,j)+u(1-v)f(i+1,j)+(1-u)vf(i,j+1)+uvf(i+1,j+1)$$

代码:

2. 图像旋转

设一幅大小为M×N的灰度图像I中，现要将其逆时针旋转 A度，得到图像J，请写出J的生成算法。【应含多种角度，锐角、钝角；应有灰度图像及彩色图像的旋转】【参考函数：imrotate】

图像变换包括两个基本操作：

1. 坐标的空间变换。
2. 像素灰度赋值

坐标变化的具体步骤如下：

• 先将原图的图像坐标系转换为数学坐标系

  假设某个点$(x_0,y_0)$图像的宽为$M$，高为$N$。转换成旋转变换的空间坐标变换：

  $$\left[\begin{array}{ccc}{x}_1& y_1& 1\end{array}\right]=\left[\begin{array}{ccc}{x}_0& y_0& 1\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& -1& 0\\ -0.5M& 0.5N& 1\end{array}\right]$$

• 在数学坐标系下使用旋转坐标变换矩阵进行旋转计算

  $$\left[\begin{array}{ccc}{x}_2& y_2& 1\end{array}\right]=\left[\begin{array}{ccc}{x}_1& y_1& 1\end{array}\right]\left[\begin{array}{ccc}\cos A& \sin A& 0\\ \sin A& -\cos A& 0\\ 0& 0& 1\end{array}\right]$$

• 再将坐标转变回图像坐标系，$M^{\prime }$表示旋转后图像的宽，$N^{\prime }$表示旋转后图像的高

  $$\left[\begin{array}{ccc}{x}_3& y_3& 1\end{array}\right]=\left[\begin{array}{ccc}{x}_2& y_2& 1\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& -1& 0\\ 0.5M’& 0.5N^{\prime }& 1\end{array}\right]$$

像素灰度赋值主要有最近邻插值和双线性插值. 一般使用效果更好的双线性插值方法.

代码:

3. 插值

在图像几何变换中，最近邻插值、双线性插值的基本原理是什么？如何实现？
最近邻插值:
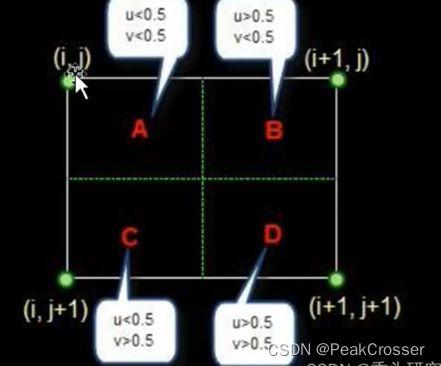
在四个像素点上划分为四个区域 A B C D 如下图所示, 然后插值到 A 区域的点，其像素值等于坐标 $(i,j)$ 的像素值，插值到 B 区域的点，其像素值等于坐标 $(i+1,j)$ 的像素值，插值到 C 区域的点，其像素值等于坐标 $(i,j+1)$ 的像素值，插值到 D 区域的点，其像素值等于坐标 $(i+1,j+1)$ 的像素值。

双线性插值:
是由两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。已知 $Q_{11}(x_1,y_1),Q_{12}(x_1,y_2),Q_{21}(x_2,y_1),Q_{22}(x_2,y_2)$ 四个点的像素值 ，现在要求点P的像素值；先根据点 $Q_{12}$ $Q_{22}$求出 $R_2$ 的像素值以及根据点 $Q_{11}$ $Q_{21}$求出 $R_1$ 的像素值，然后根据 $R_2$ $R_1$的像素值求出 P 的像素值，其过程分为两次单线性插值求出 P 的像素值。

在 x 方向做插值:
$$f(R_1)=f(x,y_1)\approx \frac{x_2-x}{x_2-x_1}f(Q_{11})+\frac{x-x_1}{x_2-x_1}f(Q_{21})$$
$$f(R_2)=f(x,y_2)\approx \frac{x_2-x}{x_2-x_1}f(Q_{12})+\frac{x-x_1}{x_2-x_1}f(Q_{22})$$
在 y 方向做插值:
$$f(x,y)\approx \frac{y_2-y}{y_2-y_1}f(R_1)+\frac{y-y_1}{y_2-y_1}f(R_2)$$
综合起来:
$$\begin{array}{rl}f(x,y)& \approx \frac{y_2-y}{y_2-y_1}f(R_1)+\frac{y-y_1}{y_2-y_1}f(R_2)\\ & =\frac{y_2-y}{y_2-y_1}(\frac{x_2-x}{x_2-x_1}f(Q_{12})+\frac{x-x_1}{x_2-x_1}f(Q_{22}))+\frac{y-y_1}{y_2-y_1}(\frac{x_2-x}{x_2-x_1}f(Q_{12})+\frac{x-x_1}{x_2-x_1}f(Q_{22}))\end{array}$$

代码:

三. 图像灰度变换

1. 直方图均衡化

设一幅大小为 M×N 的灰度图像 I 中，灰度为 g 的像素数为 h(g), $0\le g\le 255$. 请写出对图像I进行直方图均衡化，得到图像 J 的计算方法。【参考函数：histeq】

1. 计算原灰度图像 I 中每个灰度 $g_i$ 对应的频率 $p(g_i)=h(g_i)/(M\times N),i=0,1\dots 255$
2. 计算 $p(g_i)$ 的累积概率：$s_i={\sum }_{j=0}^{i}p(g_j)$
3. 原图像 I 中灰度为 $g_i$ 的点映射到新图像 J 中的灰度值是 $s_i$。将 $s_i$ 恢复到 0-255，记为 $h$：$h=round(255\ast s_i)$，四舍五入
4. 映射回原图像像素的坐标的灰度值。

代码:

%I=imread('tire.tif');myhisteq(I);
function [out_image ] = myhisteq(input_image )
    % input_mage输入图像，out_image直方图均衡化后的图像
    [h,w]=size(input_image);num=zeros(1,256);out_image=input_image;
    for i=1:h
        for j=1:w
            k = input_image(i,j);
            num(k+1)= num(k+1)+1;
        end
    end
    num = num/(h*w);
    for i=2:256
        num(i)=num(i-1)+num(i);
    end
    num = uint8(255 * num+0.5);
    for i=1:h
        for j=1:w
            out_image(i,j)=num(input_image(i,j)+1);
        end
    end
end

2. 直方图规定化

设一幅大小为M×N的灰度图像I中，灰度为g的像素数为h(g), $0\le g\le 255$。另给定一个直方图t(g), $0\le g\le 255$ 。 请写出对图像I进行变换的方法，使得变换后的新图像的直方图与t相同（近似相等）。

1. 对原灰度图像 I 进行直方图均衡化处理，求出每个灰度级 $g_i$ 对应的变换灰度 $s_i，i=0,1\dots 255$；
2. 对给定直方图 $t(g)$ 进行直方图均衡化处理（把灰度级 $g_i$ 记作 $z_i$）, 求出每个灰度级 $z_i$ 对应的变换灰度 $v_i$；
3. 找出 $s_i\approx v_i$ 的点对，并映射到 $z_i$；再利用 $s_i$ 和 $g_i$ 的对应关系得到原图灰度 $g_i$ 和目标灰度 $z_i$ 的关系：
   • 如果采用单映射规则（SML），则对原图像的每一个灰度级 $r_i$ 对应的 $s_i$ 与模板图像 $t$ 的所有变换灰度 $v_j(j=0,1,\dots 255)$ 做差值并取绝对值 $|s_i-v_j|$，比较运算结果，差值绝对值的最小值对应的变换灰度 $v_j$ 就是原图灰度 $r_i$ 对应的直方图规定化的灰度值；
   • 如果采用组映射规则（GML），则对模板图像 $t$ 的每一个变换灰度 $v_i$ (从灰度概率不为 0 开始)与原图像的所有变换灰度 $s_j(j=0,1,\dots 255)$ 做差值并取绝对值 $|v_i-s_j|$，找出差值绝对值最小值对应的原始图像灰度级 $j$。将该灰度级与上一次映射灰度级之间的原始图像灰度级都映射为模板图像中与之差值绝对值最小的灰度级。
     

代码:

function [out_image] = myhismap(input_image,match_image,option)
    % option=1表示选择单映射规则(SML)；option=2表示选择组映射规则(GML)
    [h1,w1]=size(input_image);[h2,w2]=size(match_image);
    num_image=zeros(1,256);num_match=zeros(1,256);
    for i=1:h1
        for j=1:w1
            num_image(input_image(i,j)+1)=num_image(input_image(i,j)+1)+1;
        end  
    end
    for i=1:h2
        for j=1:w2
            k = match_image(i,j);
            num_match(k+1)= num_match(k+1)+1;
        end
    end
    num_image = num_image/(h1*w1);num_match = num_match/(h2*w2);
    for i=2:256
        num_image(i)=num_image(i-1)+num_image(i);num_match(i)=num_match(i-1)+num_match(i);
    end
    num_image=uint8(255 * num_image+0.5);num_match = uint8(255 * num_match+0.5);
    out_image=input_image;
    if option == 1
        dist=zeros(256,256);
        for i = 1:256
            for j=1:256
                dist(i,j)=abs(num_image(i)-num_match(j));
            end
        end
        [m,index] = min(dist,[],2);
        index = index -1;
        for i=1:h1
            for j=1:w1
                out_image(i,j)=index(input_image(i,j)+1);
            end
        end
    else if option ==2
        index = zeros(1,256);
        for i=1:256
            if num_match(i) ~= 0
                temp=1;
                m=abs(num_match(i)-num_image(1));
                for j = 2:256
                    k = abs(num_match(i)-num_image(j));
                    if k 

3. 自适应直方图均衡化

请描述自适应直方图均衡化的实现算法。
移动模板 $W$ 在图像 $A$ 上逐行移动，并且模板 $W$ 的中心 $c(x_0,y_0)$ 对应图像上的点 $f(x_0,y_0)$；计算模板 $W$ 区域的直方图均衡化变化关系：$g(x,y)=T(f(x,y))$，计算模板中心点 $c(x_0,y_0)$ 的均衡化对应像素值：$g(x_0,y_0)=T(f(x_0,y_0))$。用 $g(x_0,y_0)$ 替代 $f(x_0,y_0)$; 逐行计算得到整幅图像的自适应直方图均衡化图像。

将图片分割成多个块（块的大小可以自定义，一般设定8×8的块，无法整除可以使用边界填充padding），然后遍历计算各个块的像素的灰度累积分布函数，最后使用插值方法来计算每个像素点对应的变换灰度。具体插值计算如下图所示：

图中将原图划分为4×4区域，它可以分为三类：蓝色像素区域表示图像的中间部分，红色像素区域是图像的四个角，绿色像素区域是图像边缘部分。蓝色区域的像素点采用相邻四个区域的灰度变换的双线性插值，绿色部分使用相邻两区域的灰度变换的线性插值，红色部分直接使用块所在的累积灰度变换函数。

4. 直方图均衡化方法的优缺点分析

设有一细胞图像，图像中大部分像素为较黑的背景，细胞中含有灰度不同的成份，若想更好的看清细胞部分，能否使用直方图均衡化方法，为什么？
可以用直方图均衡化的方法。理由如下：
当图像的灰度分布不均匀，出现过亮过暗，或者对比度过低的情况时，图像细节不明显，肉眼观察时会丢失一些信息。这时可以使用直方图均衡技术对图像进行变换，变成肉眼易于分辨的细节分明的图像。直方图均衡导致的对比度增强足以补偿图像在视觉上难以区分灰度级的差别。在给出原始图像间的重要对比度差别后，该例说明了直方图均衡作为自适应对比度增强工具的强大作用。

5. 图像灰度的对数 / 指数变换

设一幅图像整体偏暗，在暗区中不同对象较难分辨。为了增强暗区中的对象，应选用灰度的对数变换，还是指数变换？灰度变换的公式是什么？
应选用灰度的对数变换，对数变换将图像的低灰度值部分扩展，将其高灰度值部分压缩，以达到强调图像低灰度部分的目的；同时可以很好地压缩像素值变化较大的图像的动态范围，目的是突出需要的细节。

灰度对数变换公式: $s=c\log (1+r)$

• $r$ 表示原始图像的灰度级
• $s$表 示变换后的灰度级
• $c$ 为常数。

灰度指数变换公式: $s=c{r}^{\gamma }$

• $c$ 和 $\gamma$ 是正常数
• $r$ 是原始图像的灰度级
• $\gamma <1$ 时, 函数曲线在正比函数上方, 提高灰度级, 使图像变亮
• $\gamma >1$时, 函数曲线在正比函数下方, 降低灰度级, 使图像变暗

6. 图像灰度的分段线性拉伸

对一幅灰度图像，给出灰度分段线性变换方法，使得新图像中 5% 的像素的灰度变为 0， 5%的像素灰度变为 255。
设图像大小为 $M\times N$，5%的像素个数为 $5\%\times M\times N$，记为 $A$。

1. 计算图像中每个灰度级 $r$ 的像素数 $P(r)$
2. 计算灰度级 $i$ 对应的累积像素个数 ${\sum }_{r=0}^{r=i}P(r)$ 和逆序累积像素个数 ${\sum }_{r=i}^{r=255}P(r)$
3. 分别找出 $A$ 和 ${\sum }_{r=0}^{r=i}P(r)$，${\sum }_{r=i}^{r=255}P(r)$ 最接近时(即 ${\sum }_{r=0}^{r=a}P(r)\approx A$ ${\sum }_{r=b}^{r=255}P(r)\approx A$) 对应的灰度值 $a,b$。
4. 设原来灰度值为 $r$，变换后的灰度为 $g$。使用如下公式进行灰度变换：
   $$g=\{\begin{array}{ll}0,& 0\le r\le a\\ \frac{255}{b-a}(r-a),& a<r<b\\ 255,& b\le r\le 255\end{array}$$