GCN(Graph Convolutional Netwok)公式推导

理解GCN理论图卷积神经网络推导的主要资料（文章中很多内容都是出自以下文章）：
文章：https://www.zhihu.com/question/54504471/answer/332657604
https://blog.csdn.net/SperNijia/article/details/106724939
视频：https://www.youtube.com/watch?v=M9ht8vsVEw8&t=1913s
https://www.bilibili.com/video/BV1Vw411R7Fj/?spm_id_from=333.880.my_history.page.click

推导中用到的一些基础知识

特征值与特征向量：Aμ=λμ \qquad (μ为A的特征值，λ为A的特征向量)
实对称矩阵有性质：UU^T=E \qquad 则上式转化为（右边同乘U^T）得到：A=U∧U^T \qquad (U为A的特征向量组成的特征矩阵，∧为A的特征值组成的对角矩阵)
半正定矩阵性质：半正定矩阵的特征值君大于等于0
二次型：X^TAX
瑞利商：X^TAX/X^TX \qquad (A的二次型与单阵的比值)
瑞利商与特征值之间的关系：

########

Graph

GCN中的图（如下），是指数学中的用定点及边建立关系的拓扑图，用来处理非欧式距离的数据。

无向图的定义

无向图表示：G=(V,E)
V为无向图的顶点集合
E为无向图边的集合

邻接矩阵(adjacency matrix)A:
A∈R^N×N
A中矩阵元素，若两点之间存在相邻的边，则不为0（为1或者权重）
若两点之间没有相连的边，则为0

拉普拉斯矩阵

拉普拉斯矩阵：L=D-A
D为度矩阵（对角矩阵），对角矩阵上的元素${\lambda }_i$对应第i个结点的度。
A为邻接矩阵。
计算样例如下图：

在推导中还会用到的矩阵：
L$sym$=D^-1\2LD^-1\2,是对L的对称规范化（归一化）

拉普拉斯矩阵的性质

1. L以及L$sym$都是实对称矩阵，于是有：L=U∧U^T
2. L以及L$sym$都是半正定矩阵(下图第一张)
3. L$sym$特征值范围为[0,2]（下图第二张，切比雪夫多项式做卷积函数时会用到）
   
   

卷积（Convolutional）

图卷积学习链接：
https://www.zhihu.com/question/22298352#!
离散卷积：翻转再加权求和。但是在GCN中，参数本来就是未知的，所以不反转也是一样的。
连续卷积：先翻转，再求乘积的积分。

傅里叶变换

傅里叶分析之掐死教程（完整版）链接：https://zhuanlan.zhihu.com/p/19763358
以下是个人理解，如有不对请留言指出来：
傅里叶变换（简单的理解）：同一个事物在不同域里的视角是怎样的

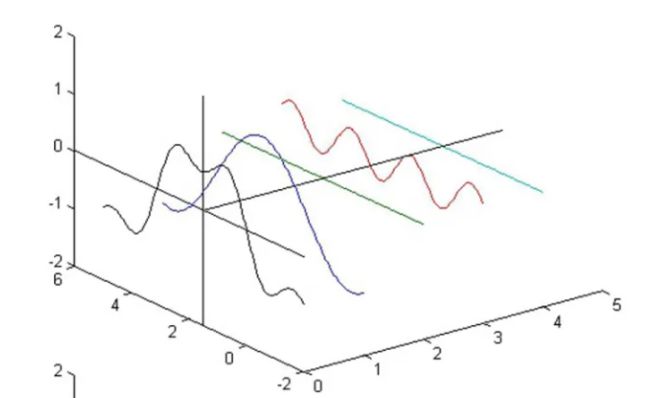
左边黑色的线经傅里叶变化为右边四条线
右边四条线经傅里叶逆变换成为左边的黑线

Graph上的傅里叶变换

f：是图上的点到信号量的一种映射。f(i)表示为图上第i个结点对应的信号量。
以拉普拉斯矩阵的特征矩阵U作为傅里叶变换的基：拉普拉斯为是对称矩阵，特征向量线性无关且相互正交。可以作为基。基就相当于搞了新的坐标系一样。

将空间维度转换为图谱维度：
给定图节点的信号量x(是信号量!)，经过傅里叶变换转到频域上：$x$=U^Tx
U为单位阵，所已某一个方向的基与x的乘积就代表了x在该基上的大小。

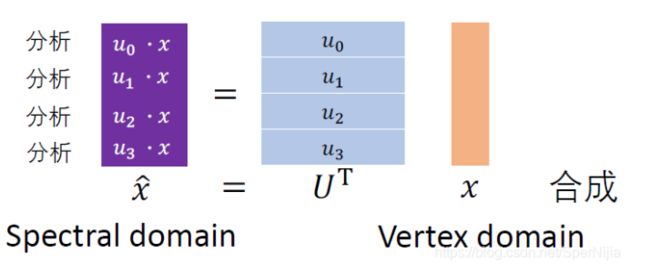
频域转换到空域：傅里叶逆变换：x=U$x$

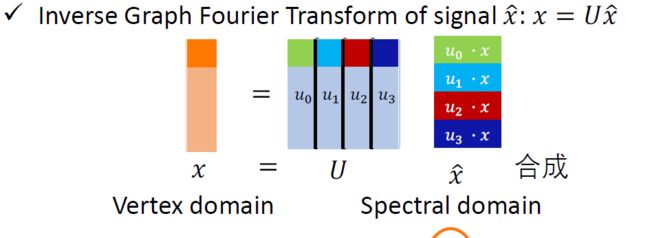
Graph上的卷积

先看下LX是什么：
LX=U∧U^TX。他其实已经实现了从空域转到频域，做卷积，再转回到空域。（从右往左看）

为什么还要用卷积核函数而不直接用拉皮拉斯矩阵呢？
应为当卷积核函数是关于∧的多项式时，就不能用一个拉普拉斯矩阵表示了

定义卷积核函数为$g_{\theta }$(∧)，（频域中的，函数形式任意）

则图上的卷积为：
信号量变换到频域中：U^Tx
卷积核函数与数据相乘：$g_{\theta }$(∧)U^Tx
转换到空域中，求出卷积：U$g_{\theta }$(∧)U^Tx

GCN公式

H^l+1=$\sigma$(U$g_{\theta }$(∧)U^TH^l)
对卷积核设计的不同,最后的通式也不相同。

第二代GCN

k等于1时，根据一阶邻居更新

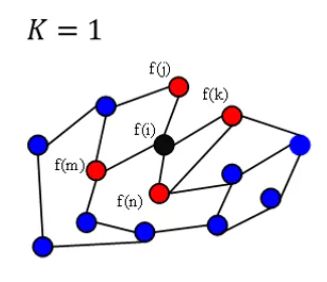
L²代表着与结点距离为2的邻居结点的信息
k等于2时，根据一阶邻居和二姐邻居更新

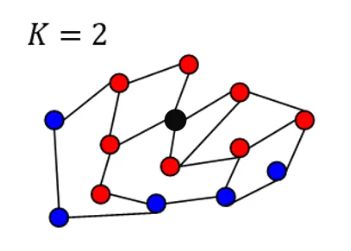
Lⁿ则代表着距离为n。
如果当n越来越大，那么图中的每一个结点会和其他的所有结点相关，这个就违反了局部性 localized。

采用切比雪夫多项式替代Lⁿ

第二个D掉了个小尖号