MWORKS.Syslab 使用攻略 | 信号处理工具箱实践-基于时差定位法的声源定位

在日常生活中，我们的耳朵会听到各种声音并进行识别定位，即所谓的“听声辨位”。有人发出声响后，人耳可以很快分辨出声音所在的方位；人耳也可轻易判断出从身边驶过的汽车的来车方向，甚至能大致知道汽车有多远；经过专业训练，人耳还可以挑战一些难度比较高的声源定位要求，例如盲人也可以踢足球。

声源定位技术是对语音或其他声音方位和位置的定位。例如，安防机器人、服务机器人、远程会议系统，在工作过程中需要对声音进行响应。安防机器人听到某个方向的声音比较大时，需要将摄像头对准该方向进行录像；服务机器人需要确定说话人的方位，以便面对服务对象进行对话；远程会议系统需要确定参会发言者位置，以便控制摄像头对发言者进行特写，将其近景视频传输至远程端，达到更好的直播效果。

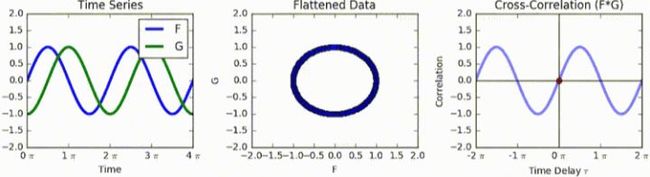
信号处理领域，互相关是两个序列的相似性的度量，作为一个序列相对于另一个序列的位移的函数，这也称为滑动点积或滑动内积。它通常用于在长信号中搜索较短的已知特征，在模式识别、单粒子分析、电子断层扫描、密码分析和神经生理学等领域都有应用。互相关在本质上类似于两个函数的卷积。

一维互相关——信号匹配

——相关性曲线

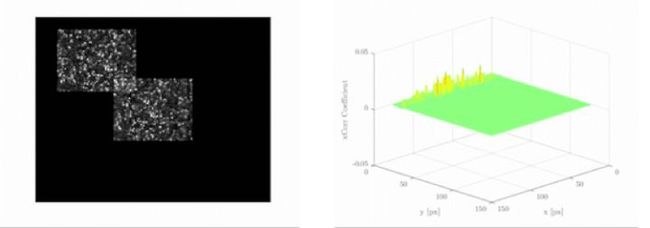
二维互相关——图像识别

——相关性曲面

声源定位算法主要有以下两大类：

1.声全息法（Holography）
Holography 算法能够重构被测物周围的整个声场，从而可以获得任何面上的声压大小分布。通过假设被测物周围符合一定声场的数学模型，麦克风阵列采集到声场中多点的声压值，从而可以解出数学模型中的未知参数，得到整个声场信息。

2.时差定位法（Time Difference of Arrival,TDOA）
TDOA 算法主要核心是计算声源到达各个麦克风的时间差，以此得到声源、麦克风相对距离用于位置估计。其中时差定位法由互相关或广义互相关算法计算得到。
 

时差定位法示例

本文以时差定位法为例作为信号处理工具箱的实践应用，下文代码及图片均为 MWORKS.Syslab 编写及生成。

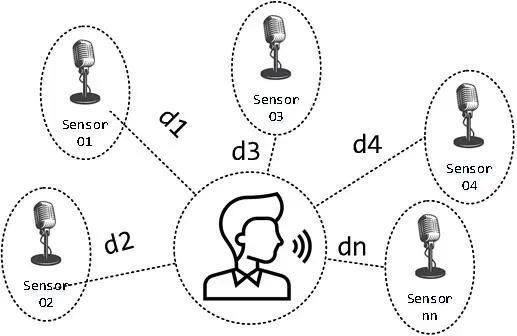
仅考虑二维平面空间，采用基于时延的声源定位算法，布置 N 个传感器进行坐标解算。

未知声源坐标 ，已知传感器、、……，传感器间时延 、 ……，为实现声源位置解算，需要至少布置三个及以上的传感器，构成有效方程个数大于未知数个数的超定方程组，并采用优化方法得到最优解。针对非线性方程数组求解的优化方法有很多，本文针对仅布置三个麦克风（下文亦称之为“传感器”），基于 NLsolve 算法包（NLsolve 为 Julia 非线性方程求解算法包），通过迭代求解非线性方程数组的数值解。

基于 TDOA 算法的多传感器定位方法

信号检测

信号检测阶段的主要目标是计算不同麦克风对同一声源信号的时延，需要依次完成采样、互相关分析、时延估计操作。

◎ 信号采样

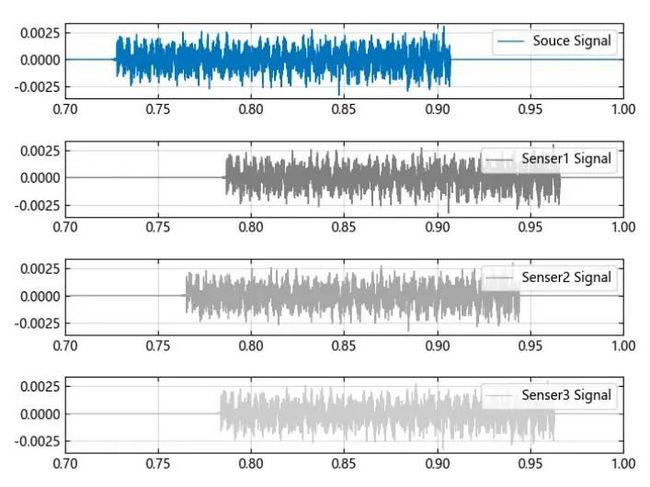
模拟声源在安静室内发出持续时间约 0.2 秒的声波，三组麦克风持续监听，并完成音频信号的采样记录，采样率越高，信号检测算法越精确，本文采用采样频率为常规 44100 Hz。
 

麦克风采样信号时域分析

◎ 互相关与时延分析

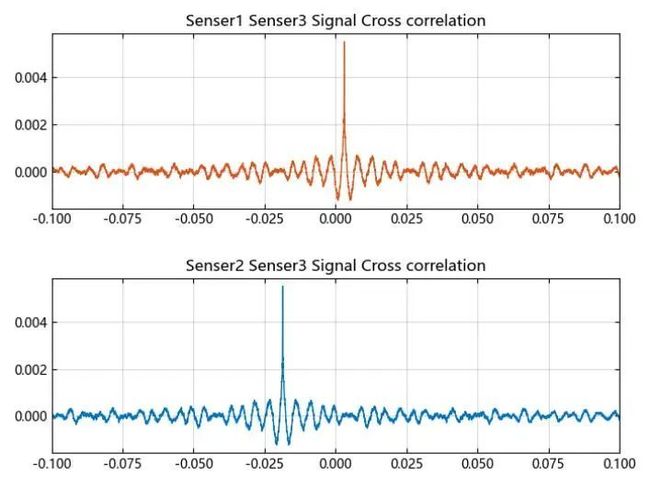
选择传感器 3 作为基准信号，用于计算接收信号的时延，基于相关性理论，采用核心函数 xcorr 对信号序列计算互相关及自相关，得到相关性分布曲线。

相关性分布曲线

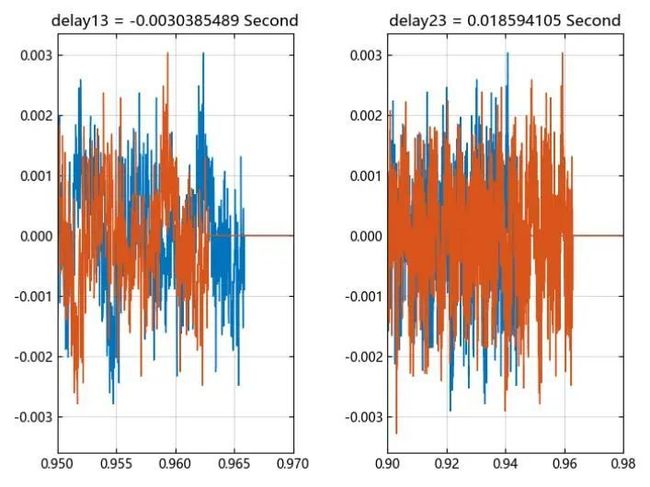
搜寻峰值相关点用于时延计算，其中对传感器 3 信号做自相关估计用于计算基准时间，对传感器 1/3、2/3 做互相关估计用于计算相对时延，因而得到传感器 1/3 时延（delay13）约 -3 微秒、传感器 2/3 时延（delay23）约为 16 微秒。

信号时延时域比较

附 Julia 计算代码：

# Julia Code
xCorr33, lags33 = xcorr(ro3)
xCorr13, lags13 = xcorr(ro1, ro3)
xCorr23, lags23 = xcorr(ro2, ro3)
_, I33 = findmax(abs.(xCorr33))
_, I13 = findmax(abs.(xCorr13))
_, I23 = findmax(abs.(xCorr23))
dealy13 = (I33 - I13) / fs
dealy23 = (I33 - I23) / fs

dealy13 = -0.0030385489
dealy23 = 0.018594105f0

声源定位

针对布置有三组麦克风的室内环境，描述声源平面坐标的方程组如下：



其中，声源坐标为，已知传感器坐标、 、 ，传感器间时延差为、 ，  为传感器  到声源的距离。

考虑麦克风信号采样及互相关算法存在一定误差，需采用优化方法求解方程组，给定声源坐标迭代初值，并寻求非线性方程最优数值解。

这里，选择 为系统状态变量  ，即：

则系统方程为：


推导关于状态变量的雅可比矩阵为:


其中，、、、 ，并且根据信号检测得到的时延结果为 =- 0.0030385489、 = 0.018594105，代入上式。

构建 F! 函数用于计算非线性系统残差，附 Julia 计算代码：

# Julia Code
function F!(F, x)
    F[1] = x[1]^2 + (x[2] - 20)^2 - (x[3] + 0.0030385489 * 340)^2
    F[2] = x[1]^2 + x[2]^2 - (x[3] - 0.018594105 * 340)^2
    F[3] = (x[1] - 30)^2 + (x[2] - 10)^2 - x[3]^2
end

构建 J! 计算系统的雅可比矩阵，附 Julia 计算代码：

# Julia Code
function J!(J, x)
    J[1, 1] = x[1] * 2
    J[1, 2] = x[2] * 2 - 20 * 2
    J[1, 3] = -x[3] * 2 - 0.0030385489 * 340 * 2
    J[2, 1] = x[1] * 2
    J[2, 2] = x[2] * 2
    J[2, 3] = -x[3] * 2 + 0.018594105 * 340 * 2
    J[3, 1] = x[1] * 2 - 30 * 2
    J[3, 2] = x[2] * 2 - 10 * 2
    J[3, 3] = -x[3] * 2
end

给定迭代算法初值，调用 NLsolve.nlsolve 函数求解。附 Julia 计算代码：

# Julia Code
result =# Julia Code
function J!(J, x)
    J[1, 1] = x[1] * 2
    J[1, 2] = x[2] * 2 - 20 * 2
    J[1, 3] = -x[3] * 2 - 0.0030385489 * 340 * 2
    J[2, 1] = x[1] * 2
    J[2, 2] = x[2] * 2
    J[2, 3] = -x[3] * 2 + 0.018594105 * 340 * 2
    J[3, 1] = x[1] * 2 - 30 * 2
    J[3, 2] = x[2] * 2 - 10 * 2
    J[3, 3] = -x[3] * 2
end nlsolve(F!, J!, [5.0; 5.0; 10.0])
Results of Nonlinear Solver Algorithm
 * Algorithm: Trust-region with dogleg and autoscaling
 * Starting Point: [5.0, 5.0, 10.0]
 * Zero: [12.002910310528083, 3.9953155842785555, 18.97238709871018]
 * Inf-norm of residuals: 0.000000
 * Iterations: 5
 * Convergence: true
   * |x - x'| < 0.0e+00: false
   * |f(x)| < 1.0e-08: true
 * Function Calls (f): 6
 * Jacobian Calls (df/dx): 6

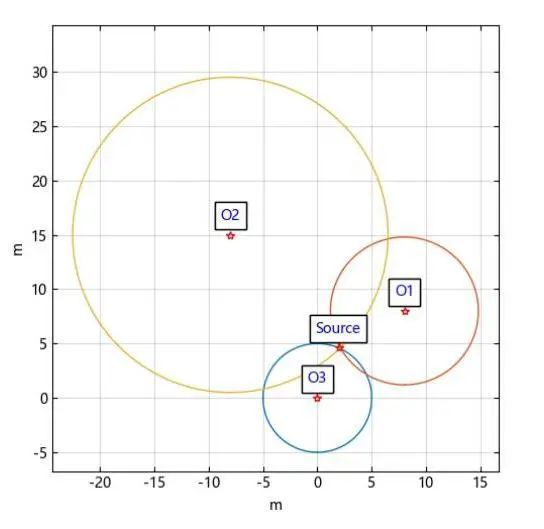
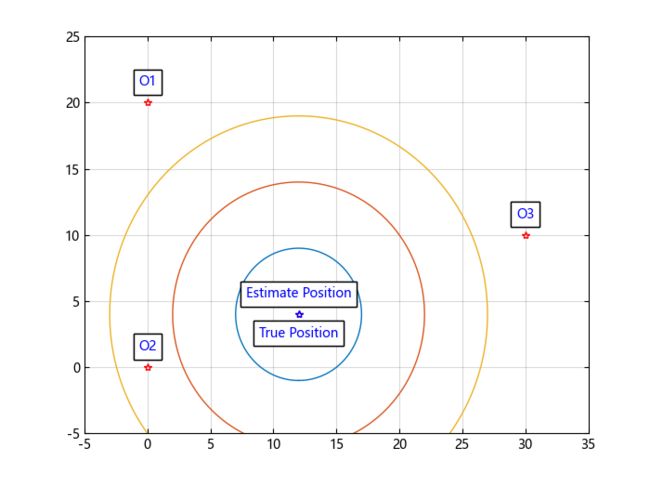
最终得到估计声源坐标 [12.002910310528083, 3.9953155842785555]，与场景中模拟的真实坐标 [12,4] 偏差为 0.005514857933001404 米。

声源位置估计

考虑到真实环境下噪声不可避免，而环境背景噪声影响互相关定位算法精度，易造成定位精度不佳，可以为此引入信号滤波算法，估计声源信号的频率范围，使用带通滤波器 bandpass 函数过滤非相关频率噪声，可以在一定程度上提高算法鲁棒性，由于篇幅限制，不在本文介绍。

信号处理工具箱（TySignalProcessing）是 MWORKS.Syslab 推出的专业工具箱之一，由同元软控完全自主开发，提供一系列函数用于包括信号分析、预处理与特征提取，滤波器设计和分析、重新采样、平滑处理、去趋势和功率谱估计等场景。

本文以声源定位为例，简要介绍了信号处理工具箱的功能，在具体工程实践中，结合通信、DSP 系统等专业工具箱，可广泛应用在音频、图像、医疗、通信、安防、定位等行业。

MWORKS.Syslab 的基础版供用户免费使用，信号处理工具箱内嵌于软件安装包内，欢迎大家前往同元软控官网自行下载。官网的 MWORKS.Syslab 仅兼容 Win10 及以上系统，若需在 Win7、Linux 或其他系统上运行，请联系同元软控公司技术支持。