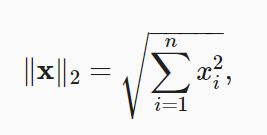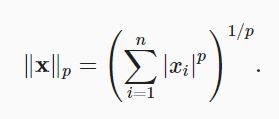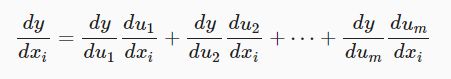李沐动手学深度学习-学习笔记之预备知识

目录

1.数据操作

1.1相关函数

1.2运算符

1.3广播机制

1.4切片

2.线性代数

2.1相关函数

2.2降维

2.3范数

3.自动微分

3.1梯度

3.2链式法则

 3.3自动求导

4.概率

---

1.数据操作

n维数组，也称为张量（tensor），张量表示由一个数值组成的数组，这个数组可能有多个维度。 具有一个轴的张量对应数学上的向量（vector）； 具有两个轴的张量对应数学上的矩阵（matrix）； （具有两个轴以上的张量没有特殊的数学名称）

1.1相关函数

先导入torch

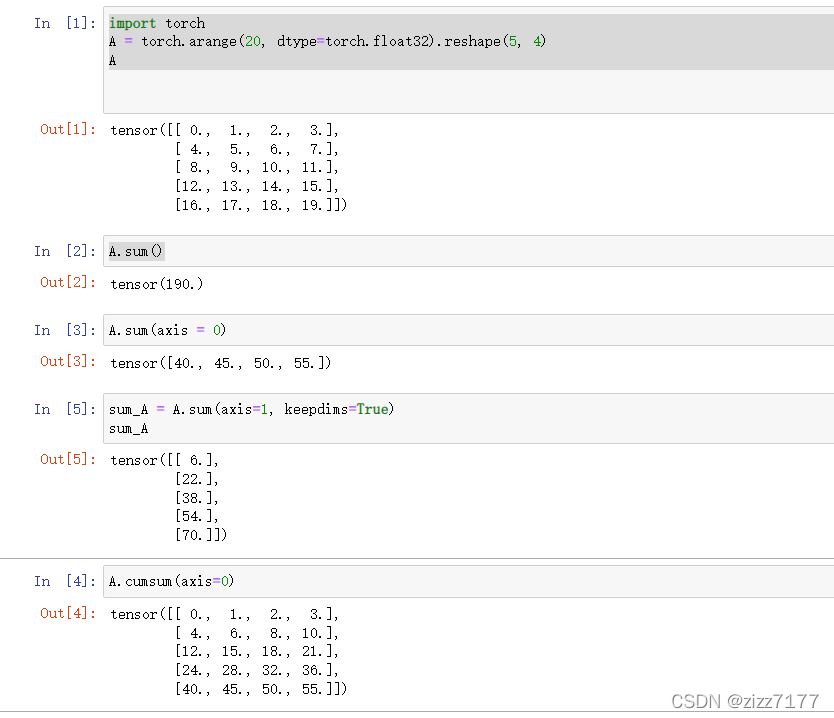
import torch

1.创建向量  →  arange （初始值为从0开始+1的浮点数）

2.访问张量形状 → shape \ 访问张量中元素总数 → numel \ 改变张量形状 → reshape

 3.创建全0、全1、高斯分布的随机数张量 → zeros、ones、randn

1.2运算符

正常的矩阵按元素运算+、-、*、/        另外 ** 为求幂运算符

对张量中所有元素求和 → sum

1.3广播机制

广播机制就是通过适当复制元素来扩展一个或两个数组， 以便在转换之后，两个张量具有相同的形状。

1.4切片

切片操作与python语法相同

X[-1]表示选择最后一个元素，X[1:3]表示选择第二个和第三个元素（  表示[1,3)  )

2.线性代数

2.1相关函数

1.访问张量长度 → len()       访问向量长度 → shanpe()

2.访问矩阵的转置  → .T

3.求张量的平均值 → mean()

4.点积 → .dot     点积是相同位置的按元素乘积的和：x⊤y=∑di=1xiyix⊤y=∑i=1dxiyi。

2.2降维

通过指定张量沿哪一个轴来通过求和降低维度。

函数：sum(axis=n) 表示沿n轴降维求和

当 keepidms=True,保持其二维或者三维的特性,(结果保持其原来维数)，默认为 False,不保持其二维或者三维的特性.(结果不保持其原来维数)

如果我们想沿某个轴计算A元素的累积总和， 比如axis=0（按行计算），我们可以调用cumsum函数。 此函数不会沿任何轴降低输入张量的维度。

2.3范数

线性代数中最有用的一些运算符是范数（norm）。 非正式地说，一个向量的范数告诉我们一个向量有多大。 这里考虑的大小（size）概念不涉及维度，而是分量的大小。

L2范数（欧式距离）                     ：

L1范数 （向量元素的绝对值之和）：

 LP范数：                                       ：

3.自动微分

3.1梯度

表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。

我们可以连结一个多元函数对其所有变量的偏导数，以得到该函数的梯度（gradient）向量。 具体而言，设函数f:Rn→Rf:Rn→R的输入是 一个nn维向量x=[x1,x2,…,xn]⊤x=[x1,x2,…,xn]⊤，并且输出是一个标量。 函数f(x)f(x)相对于xx的梯度是一个包含nn个偏导数的向量:

3.2链式法则

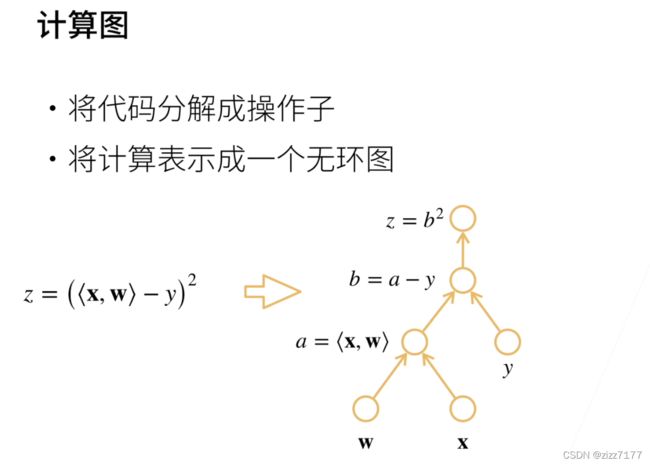
 3.3自动求导

废话不多说，直接上图

12

34

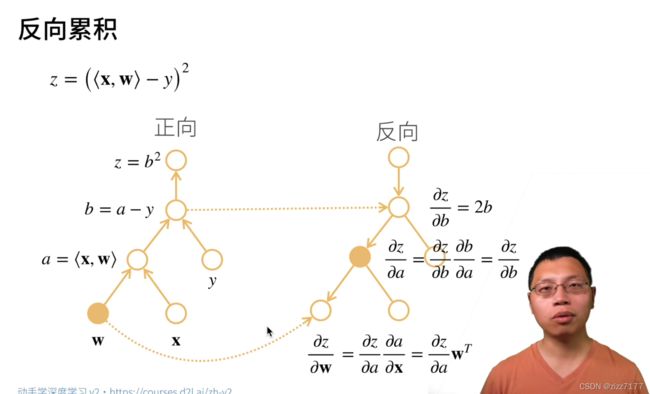
反向模式就是我们常说的BP算法，其基于的原理是链式法则。我们仅需要一个前向过程和反向过程就可以计算所有参数的导数或者梯度，这对于拥有大量训练参数的神经网络模型梯度的计算特别适合，所以常用的深度学习框架如Tensorflow其自动求导就是基于反向模式。

反向累积总结：

1. 构造计算图。
2. 前向：执行图，存储中间结果。
3. 反向：从相反执行图去除不需要的枝干。

复杂度 

计算复杂度：O(n),n是操作子个数，通常正向和方向的代价类似。

内存复杂度：O(n)，因为需要存储正向的所有中间结果。

4.概率

概率论为主，期望、方差、似然估计等等