深度学习初级阶段——全连接神经网络(MLP、FNN)
在前面的数学原理篇中,已经提到了各种深度学习的数学知识基本框架,那么从这篇文章开始,我将和大家一起走进深度学习的大门(部分图片和描述取自其他文章)。
目录
一、首先我们需要知道什么是深度学习?
二、了解神经元与感知机
三、全连接神经网络
四、神经网络框架(前向传播)实例编写
总结
一、首先我们需要知道什么是深度学习?
深度学习是机器学习领域中的一个新的研究方向,模仿生人类神经网络,学习样本数据的内在规律的一种方法,神经网络属于监督学习的过程,可以处理:回归、分类。
机器学习:数据输入——人工特征提取——分类——输出
深度学习:数据输入——神经网络特征提取和分类——输出
作用:图像识别:物体,场景,人脸识别,跟踪
自然语言处理(NLP):机器翻译,文本识别
语音技术:语言识别
主要框架:Pytorch(简单)、Tensorflow(适用工业界部署)、Mindspore(华为AI框架,脱敏)
二、了解神经元与感知机
关于神经元的介绍我就不过多赘述了,大家只需要知道感知机模型就是一个简单的人工神经网络
(这里看不懂别太纠结,后面实例将加深理解)
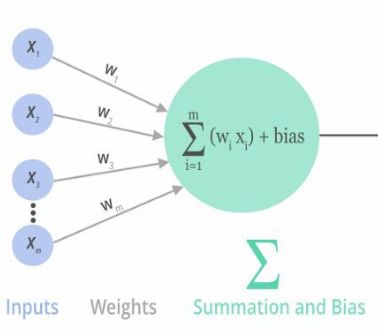
x(输入)*w(权重w,b)——>Σwx+b求和——>output(输出)
对感知机进行数学建模
#通常我们把(w,b,统一称为为W权重)
ΣW*X+b(矩阵相乘求和)(Σ求和,W权重,b偏置,x输入)
在上述的过程中感知机的输入为线性,输出也为线性,那么怎么用感知机解决非线性问题呢?
感知机模型解决线性不可分问题:感知机模型+激活函数(把线性变非线性)
说简单点就是把感知机的输出,输入到激活函数中,使其变成非线性。
其实感知机模型的完整图是这样的:
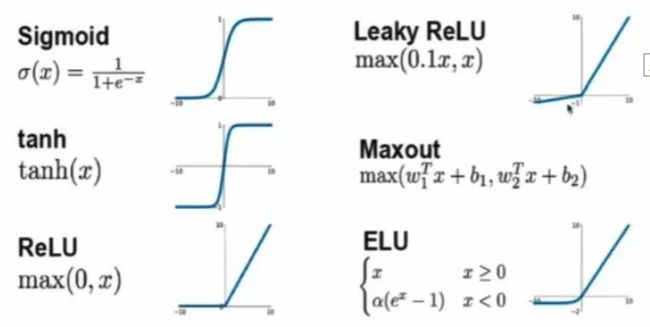
我们来看看激活函数的图像大家就明白了:
激活函数的特点:
Sigmoid:深层神经网络中极易造成梯度消失,使用于二分类问题。
Softmax:多分类问题,全概率,所有概率值加起来等于1
ReLU:不存在梯度消失(不饱和函数),丢掉不重要的特征(稀疏性),运算简单,收敛速度快,更符合生物神经网络激活机制,常用于训练过程激活函数。
为什么要使用激活函数:大家可以想像火车站排队的栏杆,激活函数就是这样不断的约束引导输入走向我们想要的目标,这才是它的底层含义,而它的用途就是把线性问题变成非线性,以及把输出映射到概率分布,方便我们进行分类。
关于激活函数详细请阅读我的文章:
实例:
(观察左边的函数)g(x)为激活函数sigoid
#在计算机套件上运行Calculator Suite - GeoGebra
实现MLP代码:
## 感知机模型实例
import numpy as np
import matplotlib.pyplot as plt
"""
#感知机是二分类的线性模型,其输入是实例的特征向量,输出的是事例的类别,分别是+1和-1,属于判别模型
1.初始话权重向量w0,可以设置为随机数等。但是要位于【-1,1】之间。
2. 指定学习率lr(步长,learning rate),介于(0,1)间。注意学习率过小,收敛速度较慢。但是如果较大,容易在达到期望输出时产生波动。
3. 开始以下迭代
3.1 计算学习信号 R = D(期望输出)-F(W'X)(训练输出)
3.2 计算权重调整 deltaW = lr*(D-R')*X
3.3 更新权重 W0 = W0+deltaW
4.不断训练直到训练输出==期望输出,或者正确率达到某个条件。
"""
def Mlp(X, Y, weight, EPOCH, lr):
# 在训练次数内,进行以下迭代
for epoch in range(EPOCH):
# 计算当前权重下的线性加权结果
out=X.dot(weight)
# 将当前线性加权结果进行sigmod
y= np.sign(out)
#梯度下降
# 根据实际输出与期望输出的差值调整权重
delatW = lr * (Y - y.T).dot(X)
# 调整权重
weight = weight + delatW
print(y)
# 判断训练输出结果和期望输出结果是否相同
if (Y == y).all():
break
return weight
if __name__ == "__main__":
# 设置训练集
X = np.array([[1, 4, 3], [1, 5, 4], [1, 4, 5], [1, 1, 1], [1, 2, 1], [1, 3, 2]])
Y = np.array([1, 1, 1, -1, -1, -1])
# 设置训练次数和学习率,初始权重([-1,1])
EPOCH= 100
lr = 0.1
np.random.seed(4)
weight = 2 * (np.random.random(3) - 0.5)
# 开始训练
W = Mlp(X, Y, weight, EPOCH, lr)
# 输出分界线并绘图
x1 = np.array([1, 6])
x2 = (-W[1] / W[2]) * x1 - W[0] / W[2]
plt.plot(x1, x2)
plt.plot(X[:, 1][0:3], X[:, 2][0:3], 'ro')
plt.plot(X[:, 1][3:6], X[:, 2][3:6], 'b*')
plt.show()
三、全连接神经网络
又称深度神经网络,多层感知机(MLP)结构,前面讲到的感知机是它的基础,就像人类的反射弧是由很多个神经元构成的,全连接神经网络也由很多个感知机构成。
全连接神经网络结构:
大家可以把每一个节点点想象成一个感知机,每个结点和下一层所有节点都有运算关系,这就是名称中‘全连接’的含义,上图的中间层也称为隐藏层,全连接神经网络通常有多个隐藏层,增加隐藏层可以更好分离数据的特征,但过多的隐藏层也会增加训练时间以及产生过拟合。
全连接神经网络训练分为前向传播、后向传播两个过程,前向传播数据沿输入到输出后计算损失函数值,后向传播则是一个优化过程,利用梯度下降法减小前向传播产生的损失函数值,从而优化、更新参数。
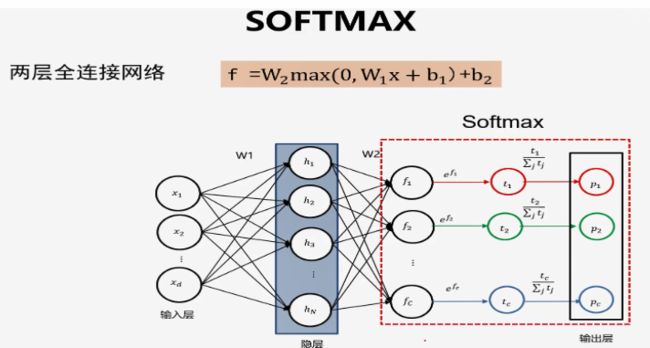
拿这个两层全连接神经网络举例,层间激活函数为RuLE,最后一层的激活函数为SoftMax。输入数据是一个3维向量,隐藏层有4个结点,意味着通过线性映射将3维向量映射为一个4维向量,最后再变为一个3维向量输出,这里需注意:softmax一般用于多分类任务中,将输出总和归一化(做多分类输出层的输出函数),从而成为预测类别的概率分布,通常之后可以接交叉熵损失函数。
 我们现在将输出结果输入到了sofmax激活函数中得到了样本的概率分布,那么如何度量神经网络分类器预测分布和真实分布之间的距离呢?
我们现在将输出结果输入到了sofmax激活函数中得到了样本的概率分布,那么如何度量神经网络分类器预测分布和真实分布之间的距离呢?
这里我们先引入了一个方法One-hot一位有效编码。类别的数量就是one-hot向量的维度,比如将三类编码为:[0,0,1]、[0,1,0]、[1,0,0]。——这里需要注意我们是对真实值进行编码,不是预测值。
我们把样本分布转化为one-hot编码,将分类值映射到整数就可以很好的表达类别了。这里的[1,0,0]就表示三类中的bird。
度量分类器预测分布和真实分布之间的误差:用交叉熵损失函数
(上一篇文章有详细讲解: 这里就是用来衡量两个随机分布差异(作为误差))。
以上就是前向传播(fp传播)以及计算损失的过程,后面我们将逐步实现。
四、神经网络框架(前向传播)实例编写
下面我们用torch编写一个简单的(隐藏层3+输出层1)4层全连接神经网络框架
import torch#导入pytorch库
from torch import nn#神经网络模块包括卷积层、池化层以及激活函等
#封装一个全连接类
class Net_v1(nn.Module):#首先Net_v1继承自nn.Module,
#初始化函数(构造函数)
def __init__(self):
#通过super(python中的超类)完成父类的初始化。
super().__init__()
#实现全连接神经网络的定义,sequeential看成神经网络的容器
self.layer=nn.Sequential(
#输入层:img.shape
nn.Linear(1200*675*3,512),#这里的1200*675*3为图片的尺寸加层数(h,w,rgb)
#隐藏层(每一层的输入是上一层的输出
nn.Linear(512,128),
nn.Linear(128, 64),
nn.Linear(64, 32),
#输出层
nn.Linear(32,10),#由于是10分类所以最后一层为10
#激活函数
# 图片的输入是NV结构,N-批次(几张图片),V-体积(w*h*c)
# 1200*675*3,激活v,dim=1,第二个维度(0,1)取图片的体积
nn.Softmax(dim=1)
)
#前向计算(前向传播),拿到计算结果
def forward(self,x):
return self.layer(x)
if __name__ == '__main__':
net_v1=Net_v1()
x = torch.randn(1, 1200 * 675 * 3) # 传随机数测试(NV结构)
y = net_v1.forward(x)#前向传播
print(y.shape)#前向传播输出形状
print(y,torch.sum(y))#前向传播输出的tensor(概率分布),sum=1可以看出我们的输出为10个概率分布对应于是分类。通过以上的代码我们就完成了神经网络前向传框架的构建,接下来就是损失函数和反向传播的部分了(持续更新)。
五、MNIST数据集处理
在上述的前向传播的框架中,神经网络的输入是一张1200*675*3的图片输出是1*10(10类)的概率分布,那么我们如何将大量的数据集作为输入丢进神经网络里面呢?我们需要对数据集进行处理,后续我会以MNIST数据集(数据集分为训练集(train)和验证集(test))为例,为大家讲解数据集处理的相关操作。
总结
在以上的学习中,我们明白了全连接神经网络的输入(数据集TRAIN)和神经网络特征提取和分类的基本流程、最后的输出(概率分布),并编写了前向传播所需的网络框架,后面我们将学习构建损失函数和如何利用损失函数进行反向传播更新权重,另外关于文中提到了方法里面的简单的数学知识,大家可以看一下我之前的两篇文章,由于本人现学现卖,不足之处还望指正。