模型介绍-----MLP
导读:M-P 模型是一个神经元结构,但是没有参数学习的过程;感知机将训练数据进行线性划分的分离超平面,引入损失函数,利用梯度下降法对损失函数进行极小化,求感知机模型,在此并提出了学习的概念,但无法解决异或运算;多层感知机通过增加层数解决非线性问题,直到1986年Hinton提出了反向传播算法,使得训练多层网络成为可能。
参考文献:《西瓜书》、《统计学习方法》、以及知乎或 CSDN 部分博客
感知机介绍
- M-P 模型
- 感知机 (perceptron)(判别模型)----神经网络和支持向量机的基础
-
- 数据集的线性可分性
- 感知机学习策略
- 感知机学习算法
- 算法收敛性
- 对偶形式
- 多层感知机
-
- 学习策略--误差逆传播算法(BP Back-propagation)
- 缓解BP网络的过拟合
- 全局最优与局部最优
M-P 模型
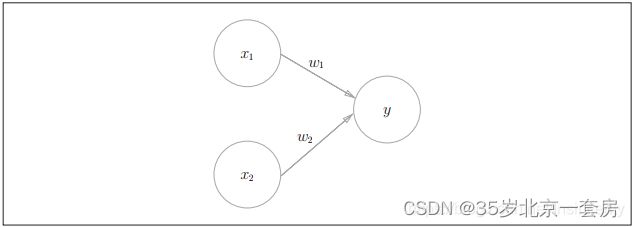
1943年,McCulloch 将生物神经网络中的神经元模型抽象为" M-P 神经元模型", n个输入( x 1 , ⋯ x n x_1, \cdots x_n x1,⋯xn),通过带权重的连接( w 1 , ⋯ , w n w_1,\cdots, w_n w1,⋯,wn)进行传递,神经元接收的总输入( ∑ w i ∗ x i \sum w_i * x_i ∑wi∗xi)与阈值 θ \theta θ 比较,然后通过激活函数处理以产生神经元的输出。激活函数包括:跃阶函数(0,1,不连续、不光滑),Sigmoid 函数((0,1)挤压函数)
感知机 (perceptron)(判别模型)----神经网络和支持向量机的基础
在1957年,美国学者Frank Rosenblatt 提出感知机,一种二值分类的线性分类模型,(特征向量)->实例类别(+1,-1),旨在将训练数据进行线性划分的分离超平面,导入基于误分类的损失函数,利用梯度下降法对损失函数进行极小化,求感知机模型。
以线性为例,由两层神经元组成 x 1 x_1 x1, x 2 x_2 x2为两个神经元,可以实现与、或、非运算。( x 1 ∧ x 2 x_1 \land x_2 x1∧x2),( x 1 ∨ x 2 x_1 \vee x_2 x1∨x2),( x 1 ¬ x 2 x_1 \neg x_2 x1¬x2)
![]()
其中 w w w 和 b b b 为感知机模型参数, w ∈ R n w \in R^n w∈Rn 表示权值(weight)或权值向量(weight vector), b ∈ R b\in R b∈R 叫作偏置(bias), w ⋅ x w\cdot x w⋅x 表示 w w w 和 x x x 的内积。sign 是符号函数,即:
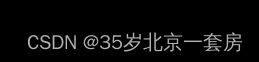

超平面 S S S,其中 w w w 超平面的法向量, b b b 是超平面的截距。超平面将特征空间划分为两个部分。位于两部分的点(特征向量)分别被分为正、负两类。
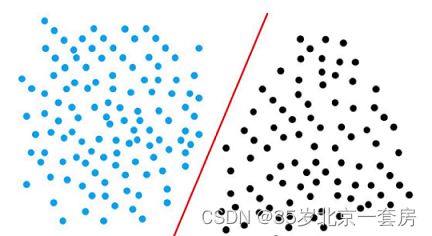
数据集的线性可分性
如果存在这样一个超平面,可以将数据集的正负实例点完全正确地划分到超平面的两侧。
1969 Minsky 证明若两类模式是线性可分的,即存在一个线性超平面将他们分开,则感知机的学习过程一定会收敛,否则会震荡,不能求得合适的解。
感知机学习策略
-
确定超平面( w w w/ b b b), 定义一个损失函数,并极小化。
损失函数:(1)误分类点的总数,不是参数 w w w/ b b b的连续可导函数,不易优化;(2)用距离来测量,误分类点到超平面的总距离。(点到直线的距离)

-
对于误分类的数据( 将1误分类为-1,或者将-1误分类为1 ), − y i ( w ∗ x i + b ) > 0 -y_i(w*x_i+b)>0 −yi(w∗xi+b)>0, 当 w ∗ x i + b > 0 w*x_i+b>0 w∗xi+b>0, y i < 1 y_i <1 yi<1, 误分类的集合为M, 误分类点到超平面 S S S的总距离为

感知机学习算法
感知机学习问题转化为求解损失函数的最优化问题,最优化方法随机梯度下降。
首先,任意选取一个超平面 w 0 w_0 w0, b 0 b_0 b0 ,然后用梯度下降法不断地极小化目标函数。极小化过程中不是一次使 M M M中所有误分类点的梯度下降,而是一次随机选取一个误分类点使其梯度下降。
对 w w w, b b b更新:
![]()
![]()
算法:
输入: 训练数据集
输出: w, b; 感知机模型 f ( x ) = s i g n ( w ∗ x + b ) f(x)=sign(w*x+b) f(x)=sign(w∗x+b)
(1) 选取初值 w 0 , b 0 w_0,b_0 w0,b0
(2) 在训练集中选取数据 (x_i,y_i)
(3) 如果 y i ( w ∗ x i + b ) ≤ 0 y_i(w*x_i+b)\leq0 yi(w∗xi+b)≤0
(2.6),(2.7)
(4) 转至(2),直至训练集中没有误分类点。
当一个实例点被误分类,及位于分离超平面的错误一侧时,则调整 w , b w, b w,b 的值,使分离超平面向该误分类点的一侧移动,以减少该误分类点与超平面的距离,直至超平面越过该误分类点使其被正确分类。(与、或、非门都支持)
算法收敛性
误分类的次数k是有上界的,经过有限次搜索可以找到将训练数据完全分开的分离超平面,也就是说,当训练数据集线性可分时,感知机学习算法原始形式迭代是收敛的。
对偶形式
将 w w w 和 b b b 表示为实例 x i x_i xi和 y i y_i yi的线性组合的形式,通过求解其系数而求得 w 和 b 。
![]()
![]()
逐步修改 w w w 和 b b b,设修改 n n n 次,则w , b 关于 ( x i , y i x_i,y_i xi,yi) 的增量分别是 α i y i x i \alpha_i y_i x_i αiyixi 和 $\alpha_i y_i $,这里 α i = n i η \alpha_i = n_i \eta αi=niη , 最后的 w , b 可以分别表示为


表示第 i i i 个实例点由于误分而进行更新的次数,实例点更新次数越多,意味着它距离分离超平面越近,也就越难正确分类, 这样的实例对学习结果影响最大。
多层感知机
解决非线性可分问题,使用多层功能神经元,使用两层感知机解决异或问题。神经元不存在同层相连,也不存在跨层连接。
特点:
- 参数量大,层数多
- 丢失像素间空间信息,只接受向量输入
学习策略–误差逆传播算法(BP Back-propagation)
具体公式在西瓜书上,我的理解还是利用链式法则,从输入到输出的你过程。
训练集 D = ( x i , y i ) D=(x_i,y_i) D=(xi,yi), x i ∈ R d , y i ∈ R l x_i\in R^d, y_i \in R^l xi∈Rd,yi∈Rl, 输入为d维,输出为l维, 隐藏层的第h个神经元阈值为 γ h \gamma_h γh, 输出层的第j个神经元阈值为 θ j \theta_j θj
BP算法目标的最小化训练集D上的累积误差
E = 1 m ∑ k = 1 m E k E = \frac{1}{m}\sum^m_{k=1}E_k E=m1∑k=1mEk
三种激活函数:ReLU函数,Sigmoid函数,tanh函数
R e L U ( x ) = m a x ( x , 0 ) ReLU(x)=max(x,0) ReLU(x)=max(x,0), 只保留正数元素,并将负数元素清零
Sigmoid 函数可以将元素的值变换到0和1之间, s i g m o i d ( x ) = 1 / ( 1 + e x p ( − x ) ) sigmoid(x)=1/(1+exp(−x)) sigmoid(x)=1/(1+exp(−x))
tanh函数是将元素值变换到-1和1之间, t a n h ( x ) = ( 1 − e x p ( − 2 x ) ) / ( 1 + e x p ( − 2 x ) ) tanh(x)=(1−exp(−2x))/(1+exp(−2x)) tanh(x)=(1−exp(−2x))/(1+exp(−2x))
用于分类器时,Sigmoid 函数及其组合通常效果更好。由于梯度消失问题,有时要避免使用 Sigmoid 和 tanh 函数。
在神经网络层数较多的时候,最好使用 ReLu 函数,ReLu函数比较简单计算量少,而 Sigmoid 和 Tanh 函数计算量大很多。
![]()
这幅图引自博客(https://blog.csdn.net/u011848397/article/details/102733351)
缓解BP网络的过拟合
- “早停”, 数据分为训练集和验证集,训练集计算梯度、更新连接权和阈值,验证集估计误差,若训练集误差下降,而验证集误差升高,则停止训练
- 正则化,在误差目标函数中增加一个用于描述网络复杂度的部分,
E = 1 m ∑ k = 1 m E k + ( 1 − λ ) ∑ i w i 2 E = \frac{1}{m}\sum^m_{k=1}E_k + (1-\lambda)\sum_i w^2_i E=m1k=1∑mEk+(1−λ)i∑wi2
全局最优与局部最优
- 以多组不同参数值初始化多个神经网络
- 利用模拟退火技术,以一定的概率接收比此次结果更差的结果
- 随机梯度下降