数据分类：支持向量机

一、作业要求

1. 编写SVM算法程序（可从网络查找相应代码），平台自选。
2. 使用SVM 算法，分别用三种核函数对给定样本数据集建立分类模型。其中数据文件中维度“类型”为标识的类型。
3. 用60%的数据为训练集，40%为测试集，用准确度、灵敏度和特效性检验你的结果。
4. 完成挖掘报告。

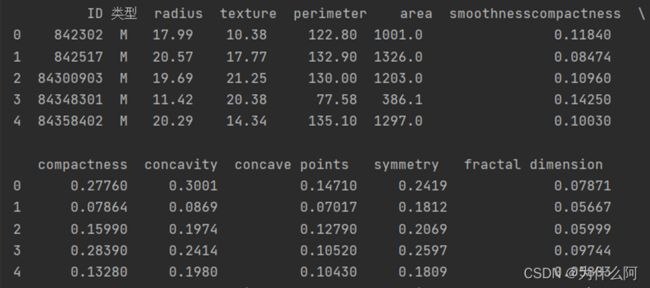
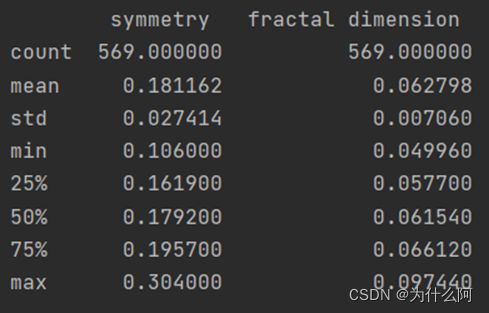
二、数据集预分析

1. 数据集前五条展示
   

2. 查看数据集的整体信息
   整个数据集共12列，569行，无缺失值，不需要做缺失值处理。
   

3. 数据集列的注释
   包括ID，类型与特征共12个
   

4. 查看数据各特征下平均值，方差，最值，四分位数等指标值
   
   
   

5. 数据两种类型分布情况可视化
   

三、数据预处理

1. 特征选择
   
   热力图对角线上的为单变量自身的相关系数是1，颜色越浅代表相关性越大。观察热力图可见radius_mean、perimeter_mean 和 area_mean 相关性非常大，compactness_mean、concavity_mean、concave_points_mean这3个字段也是相关的，因此可选择radius_mean，perimeter_mean，area_mean，compactness_mean，concavity_mean，concave_points_mean这六个特征作为最主要特征。

四、相关知识

1. SVM核函数
   ① 线性核函数
   线性核函数（Linear Kernel）其实就是线性可分SVM，也就是说，线性可分SVM可以和线性不可分SVM归为一类，区别仅仅在于线性可分SVM用的是线性核函数。
   
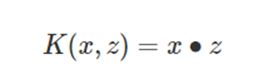
   ② 高斯核函数
   高斯核函数（Gaussian Kernel），在SVM中也称为径向基核函数（Radial Basis Function,RBF），它是非线性分类SVM最主流的核函数，是libsvm默认的核函数。
   
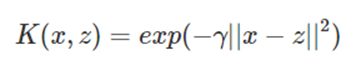
   ③ Sigmoid核函数
   Sigmoid核函数（Sigmoid Kernel）也是线性不可分SVM常用的核函数之一。
   
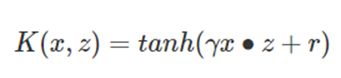
2. SVM性能度量指标
   ① 混淆矩阵
   针对二分类问题，通常将我们所关心的类别定为正类，另一类称为负类。混淆矩阵由如下数据构成：
   True Positive (真正，TP)：将正类预测为正类的数目
   True Negative (真负，TN)：将负类预测为负类的数目
   False Positive(假正，FP)：将负类预测为正类的数目（误报）
   False Negative(假负，FN)：将正类预测为负类的数目（漏报）

	M	B
F(False,0)	TN	FP
T(True,1)	FN	TP

② 准确率
准确率是最常见的评价指标，预测正确的样本数占所有的样本数的比例；通常来说，准确率越高分类器越好。

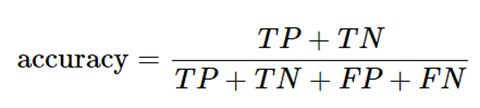
③ 敏感度（召回率）
灵敏度表示的是样本中所有正例中被识别的比例，衡量了分类器对正例的识别能力。

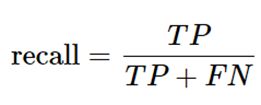
④ 特效性检验（特效度）
特效度表示的是样本中所有负例中被识别的比例，衡量了分类器对负例的识别能力。

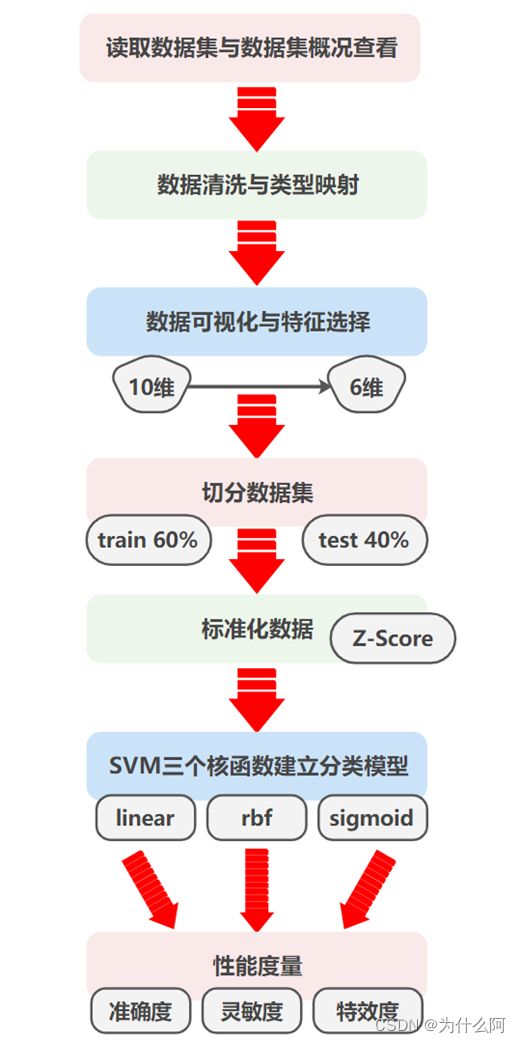
五、概要设计

概要设计流程图：

六、详细设计及核心代码

1. 读取数据集与数据集概况查看

#读取数据集
data = pd.read_excel('分类作业数据集.xlsx')
#数据集查看
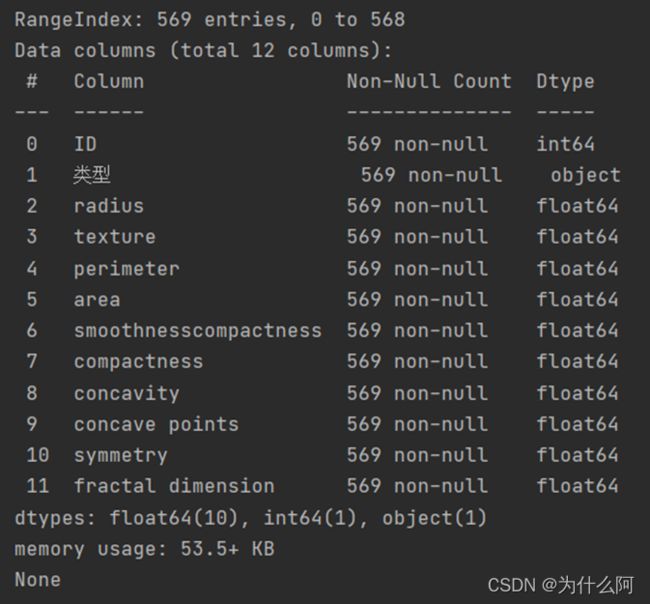
print(data.info())
print(data.columns)
print(data.head(5))
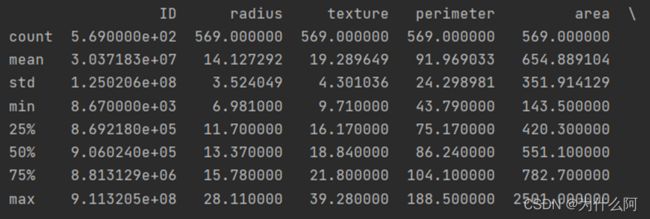
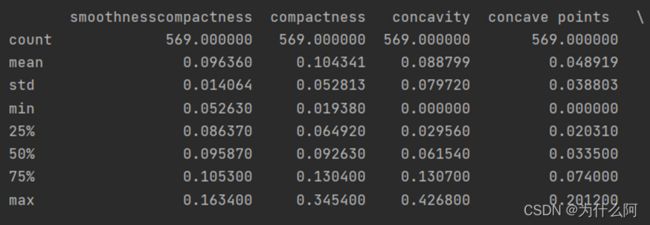
print(data.describe())

2. 数据清洗与类型映射

#数据清洗
#“ID"列没有实际意义，删除
data.drop('ID',axis = 1,inplace=True)
#将类型的B，M用0,1代替
data['类型'] = data['类型'].map({'M':1,'B':0})

3. 数据可视化与特征选择

# 特征字段放入features_mean
features_mean= list(data.columns[1:12])
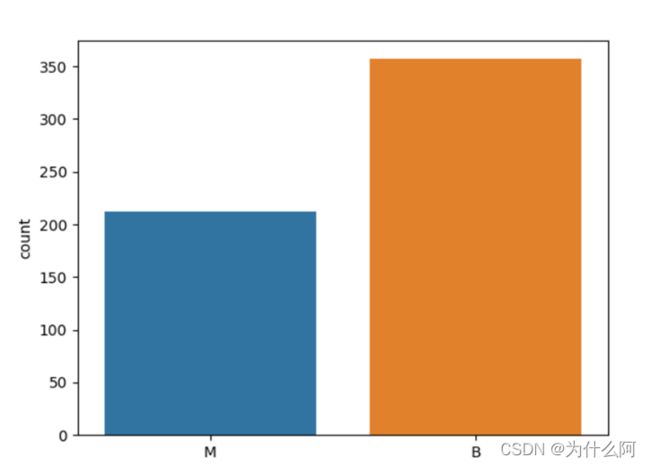
# 可视化两种类型分布
sns.countplot(x="类型",data=data)
plt.show()
# 用热力图呈现features_mean字段之间的相关性
corr = data[features_mean].corr()
plt.figure(figsize=(14,14))
# annot=True显示每个方格的数据
sns.heatmap(corr, annot=True)
plt.show()
# 特征选择后得到的6个特征
features_remain = ['radius','texture', 'smoothnesscompactness','compactness','symmetry ', 'fractal dimension ']

4. 切分数据集为训练集和测试集

#抽取40%的数据作为测试集，其余60%作为训练集
train,test = train_test_split(data,test_size = 0.4)
 #抽取特征选择的数值作为训练和测试数据
train_X = train[features_remain]   
train_y = train['类型']
test_X = test[features_remain]
test_y = test['类型']

5. 标准化数据

#采用Z-Score标准化，保证每个特征维度的数据均值为0，方差为1
ss = StandardScaler()
train_X = ss.fit_transform(train_X)
test_X = ss.transform(test_X)

6. 采用SVM三个核函数建立分类模型与性能度量

print("%%%%%%%准确度%%%%%%%")
print("%%%%%%%敏感度%%%%%%%")
print("%%%%%%%特效度%%%%%%%")
print("%%%%%%%F1_score%%%%%%%")
kernelList = ['linear','rbf','sigmoid']
for kernel in kernelList:
    svc = SVC(kernel=kernel).fit(train_X,train_y)
    y_pred = svc.predict(test_X)
    # 计算准确度
    score_svc = metrics.accuracy_score(test_y,y_pred)
    print(kernel+":")
    print(score_svc)
    # 计算召回率（敏感度）
    print(recall_score(test_y, y_pred))
    # 混淆矩阵
    C = confusion_matrix(test_y, y_pred)
    TN=C[0][0]
    FP=C[0][1]
    FN=C[1][0]
    TP=C[1][1]
    # 计算特效度
    specificity=TN/(TN+FP)
    print(specificity)

    # 计算f1_score
    # print(f1_score(test_y, y_pred))
    # print(classification_report(test_y, y_pred))

七、运行截图

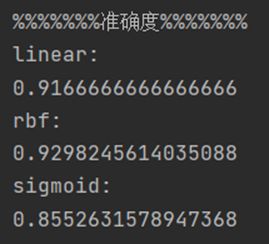
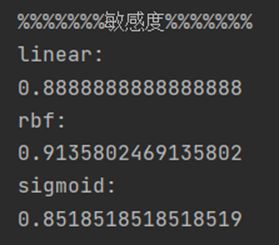
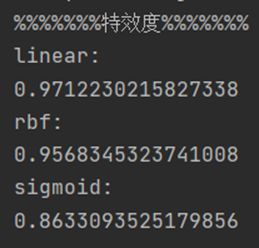
以下分别是三个核函数模型的准确度，敏感度，特效度结果：

为了更直观看到SVM三个核函数建立模型的性能度量值，将所得结果绘制成表格如下（保留小数点后五位）：

由表格可见，对于该数据集，核函数rbf建立的模型在准确度和敏感度上均高于其余两种核函数，特效度略低于linear核函数模型，从整体来看，核函数rbf建立的分类模型应用于该数据集性能更好。

八、完整代码

import matplotlib
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn import svm
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn import metrics
from sklearn.metrics import recall_score
from sklearn.metrics import f1_score
# 解决坐标轴刻度负号乱码
plt.rcParams['axes.unicode_minus'] = False
# 解决中文乱码问题
plt.rcParams['font.sans-serif'] = ['Simhei']
# 显示数据集的所有列
pd.set_option('display.max_columns', None)

#读取数据集
data = pd.read_excel('分类作业数据集.xlsx')
#数据集查看
print(data.info())
print(data.columns)
print(data.head(5))
print(data.describe())

#数据清洗
#“ID"列没有实际意义，删除
data.drop('ID',axis = 1,inplace=True)
#将类型的B，M用0,1代替
data['类型'] = data['类型'].map({'M':1,'B':0})
# 特征字段放入features_mean
features_mean= list(data.columns[1:12])
# 可视化两种类型分布
sns.countplot(x="类型",data=data)
plt.show()
# 用热力图呈现features_mean字段之间的相关性
corr = data[features_mean].corr()
plt.figure(figsize=(14,14))
# annot=True显示每个方格的数据
sns.heatmap(corr, annot=True)
plt.show()
# 特征选择后得到的6个特征
features_remain = ['radius','texture', 'smoothnesscompactness','compactness','symmetry ', 'fractal dimension ']

#抽取40%的数据作为测试集，其余60%作为训练集
train,test = train_test_split(data,test_size = 0.4)
train_X = train[features_remain]   #抽取特征选择的数值作为训练和测试数据
train_y = train['类型']
test_X = test[features_remain]
test_y = test['类型']

#采用Z-Score标准化，保证每个特征维度的数据均值为0，方差为1
ss = StandardScaler()
train_X = ss.fit_transform(train_X)
test_X = ss.transform(test_X)

print("%%%%%%%准确度%%%%%%%")
print("%%%%%%%敏感度%%%%%%%")
print("%%%%%%%特效度%%%%%%%")
print("%%%%%%%F1_score%%%%%%%")
kernelList = ['linear','rbf','sigmoid']
for kernel in kernelList:
    svc = SVC(kernel=kernel).fit(train_X,train_y)
    y_pred = svc.predict(test_X)
    # 计算准确度
    score_svc = metrics.accuracy_score(test_y,y_pred)
    print(kernel+":")
    print(score_svc)
    # 计算召回率（敏感度）
    print(recall_score(test_y, y_pred))
    # 混淆矩阵
    C = confusion_matrix(test_y, y_pred)
    TN=C[0][0]
    FP=C[0][1]
    FN=C[1][0]
    TP=C[1][1]
    # 计算特效度
    specificity=TN/(TN+FP)
    print(specificity)

    # 计算f1_score
    # print(f1_score(test_y, y_pred))
    # print(classification_report(test_y, y_pred))