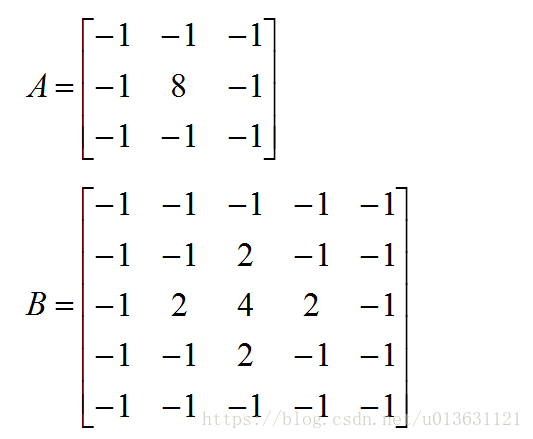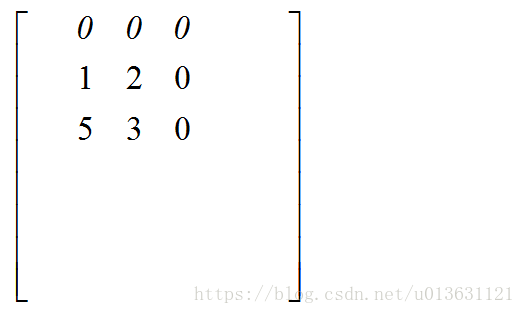白话文讲计算机视觉-第三讲-滤波器

我们今天来学习第三讲，第三讲我们主要讲解的是滤波器。滤波器听着名字倒是挺TMD高大上，但是呢，名字叫的NB不一定就真NB。比如X门大学的XX良，又是奖学金获得者，又是保研保博的人，但是她的智商捉急啊。真正的坏人都找不到，却侮辱我们中国的普通人，还说自己的母校是野鸡大学。对于这个

名字NB的XX良的评价我就到这里了，点到为止，我还是说一下什么叫做滤波器，滤波器名字顾名思义，就是能够把原始数据过滤掉一部分的一种机器。

比如有一张图：

 

这是一个123*176的灰度图片，也就是说它共有123*176=21648个点，这些点组成了一个点阵：其中点阵有123行，每行中包含176个点，而这些点的亮度不同，如果白色为255，黑色为0.灰度图的每一个点的亮度在0~255之间，也就是黑白之间，这样就是灰色，也就是灰度。如果大家想不明白，你就想一共有21648个小灯泡，全亮是白色，不亮是黑色，要是在全亮和不亮之间调节光的强度，就是一堆过渡颜色。

如果把这张图加上颜色的话，也就是我们在每一个点中放三个灯泡，这三个灯叫做BGR，也就是blue，green，red，三原色，根据三个小灯泡的亮度不同，就会组成N种颜色。因为是三个小灯牌，所以说由123*176的灰度图片变成了123*176*3的彩色图片，3中每一个123*176的点阵数据代表一个小灯泡的数值，也是0~255之间，比如B灯，0是黑色，255是蓝色。

说完图片了，我们用滤波器怎么过滤呢？我们以黑白图片举例，让大家看看滤波器的样子：

A、B就是两个滤波器，这样的滤波器也叫做高通滤波器，高通低通我后面会介绍。现在我们说一下A、B，A叫做3*3核滤波器、B叫做5*5核滤波器。这些滤波器和图片的点阵做卷积，得到的新的矩阵就是过滤后的图像。

举一个例子：

如果我们有一张4*4的图片，我们要通过一个3*3的滤波器过滤，那么怎么做呢？

（1）我们假定3*3的滤波器为：

图像点阵为：

我们首先在矩阵的外围加0，添加一圈，变成这样：

为什么是添加一圈而不是两圈，这是因为我们的滤波器是3*3的，我们让最中间的元素，也就是第二行第二列的元素，对着图像的第一个元素。然后我们发现左边少了一列，上面少了一行，同理用中间元素对着图像中第一行最后一个、最后一行第一个、最后一行最后一个，我们就会发现要添加的是一圈的0。添加完成之后，我们下一步要做的就是做卷积。怎么做？

（2）我们首先把滤波器旋转180度：

（3）然后用旋转后的滤波器中间元素对准图片的第一个元素（未加0之前），然后把图像点阵中和滤波器对应位置的值相乘，然后相加。比如第一次滤波器与图像卷积的是：

那么我们用其与滤波器相乘：0*0+0*0+0*1+0*0+1*1+2*1+0*1+5*1+3*1=11。

（4）接下来我们把滤波器往右移动一格，滤波器对应的元素变为：

我们用其与滤波器相乘：0*0+0*0+0*1+1*0+2*1+0*1+5*1+3*1+0*1=10。

（5）同理我们继续移动，直到第一行最后一格元素0被卷积计算完毕为止。这样我们得到了4个数据，我们给它拼成一行：[11,10,7,4]

（6）然后我们回到这行最开始的位置，也就是1那个位置，然后向下移动一格：

（7）然后进行卷积运算，得到新的元素为10.同理向右移动到最后一个位置，卷积后返回第二行开头，向下移动一位。以此类推直到所有的数据都被滤波器遍历到为止。我们最终得到一个新的、滤波完毕的矩阵：

（8）得到这个矩阵之后，我们的滤波就完成了，这个矩阵就是滤波后得到的新的图像啦。

我们在OPENCV中怎么让它实现呢，很简单，程序如下：

import cv2

import numpy as np

from scipy import ndimage

a = np.array([[1, 2, 0, 0],

    [5, 3, 0, 4],

    [0, 0, 0, 7],

    [9, 3, 0, 0]])

k = np.array([[1,1,1],

[1,1,0],

[1,0,0]])

aa=ndimage.convolve(a, k, output=None, mode='constant', cval=0.0, origin=0)

首先我们定义了一个4*4的矩阵（图像），这时为了方便教学小木我用矩阵来假设一章图片，而不是真正图片。然后定义了一个3*3的滤波器。接着用ndimage.convolve()这个方法求出aa矩阵，也就是就是卷积后的矩阵（图像）。我来说一下里面的参数吧，参数a,k分别指的是原始图片，图片滤波器。output指的是输出，我们用aa输出了，就写none好了，也就是不输出。mode是模式，模式有很多种： {‘reflect’,’constant’,’nearest’,’mirror’, ‘wrap’}，reflect是不添加0，而是把一边末尾的元素搬到另一边（镜像，比如左边的添加0改成把右边最后一行挪到左边），如果我们不指定是哪个，那么默认的是reflect。我们上面讲的是constant模式，也就是常量模式，所以写constant就好了。cval指的是我们在外围加什么数字，上面的例子是加0，那么就写0。origin是过滤器的位置偏移我们所选的元素中心多少，一般我们不偏移，所以写0就行，如果写其他数字，比如1，就是往左边和上面都偏移一格。

这样滤波器的原理就讲完了，接下来我说一下滤波器的种类：

滤波器按照大类来分的话有两种，一种叫做高通滤波器，另外一种叫做低通滤波器。高通滤波器我们上面已经看过几个例子了：

A和B就是高通滤波器，我们就拿A举例来说明，我们看A里面我们就会发现，A里面一共九个元素，而且这九个元素相加等于0。我们再往深里面想，我们滤波的时候，每一次卷积时候，图片的点阵对应的元素是滤波器的8，如果我们是在过滤图片的第一个元素的话，那么第一个元素乘以8，第一个元素旁边的元素就是乘以-1，然后加和。我们看看这次的加和，就是第一个元素的八倍与周围的8个元素相减。如果说图片中间的元素的值与周围的值相差很大，那么我们过滤之后，与之前原图片的值相差会很大，也就是亮度增加了，反之亮度不会增加。简单的例子是如果这个点是100，其它点都是100的话，那么结果就是0，也就是白色变成了黑色，亮度没有增加。如果点是100，其它的都是10，那么我们算出来就是720，我们的最大值是255，所以取255，这个点就是白点，高亮显示。我们把所有的点都这样之后，突出的点就会亮度变大，不突出的亮度减少。我们知道一个东西最外边缘和背景肯定值相差很大，所以这样可以提取出图片的边缘。我们写一个程序，来获取过滤前后的图片：

#导入相关的库

import cv2

import numpy as np

from scipy import ndimage

#定义一个3*3高通滤波器

kernel_3=np.array([[-1,-1,-1],

                  [-1, 8,-1],

                  [-1,-1,-1]])

#定义一个5*5高通滤波器

kernel_5=np.array([[-1,-1,-1,-1,-1],

                   [-1,-1, 2,-1,-1],

                   [-1, 2, 4, 2,-1],

                   [-1,-1, 2,-1,-1],

                   [-1,-1,-1,-1,-1]])

#导入图片

img=cv2.imread('D:/xiaomu/opencv1-1.png',0)

#显示图片

cv2.imshow('dawawa',img)

#高通滤波

k3=ndimage.filters.convolve(img,kernel_3)

k5=ndimage.filters.convolve(img,kernel_5)

#显示高通滤波后图片

cv2.imshow('dawawaK3',k3)

cv2.imshow('dawawaK5',k5)

#等待键盘按键

cv2.waitKey()

#关闭窗口并退出

cv2.destroyAllWindows()

我们发现5*5的滤波器可以很明显地把物体的轮廓从背景中描绘出来。

高通滤波器我们知道它们可以用于边缘勾画，那么低通滤波器呢？低通滤波器干的事儿是去噪声和模糊化。噪声是什么？就是我们这个图片不清晰，上面有很多的黑、白点。我们通过低通滤波器模糊化，把小黑、白点给去掉。低通滤波器一般有如下形式：

这就是一个低通滤波器，我们发现这个滤波器是一个5*5的核，然后所有值相加等于1。这说明啥呢，如果我们图像中的某一个像素点和周围像素点的差值大的话，那么这个点就会被周围的像素给 同化。比如中间值是8，其他地方都是4，那么经过卷积之后这个值就变成了4.16，和4好近哦。这样不就是同化了么，如果我们按照极端的情况想的话，8就相当于白点，一下子就没了，也就是模糊化来了。

我们写一个程序试试：

#导入相关的库

import cv2

import numpy as np

from scipy import ndimage

 

#定义一个5*5低通滤波器

kernel_5=np.array([[0.04,0.04,0.04,0.04,0.04],

                   [0.04,0.04,0.04,0.04,0.04],

                   [0.04,0.04,0.04,0.04,0.04],

                   [0.04,0.04,0.04,0.04,0.04],

                   [0.04,0.04,0.04,0.04,0.04]])

#导入图片

img=cv2.imread('D:/xiaomu/opencv1-1.png',0)

#显示图片

cv2.imshow('dawawa',img)

#低通滤波

k5=ndimage.filters.convolve(img,kernel_5)

#显示高通滤波后图片

cv2.imshow('dawawaK5',k5)

#等待键盘按键

cv2.waitKey()

#关闭窗口并退出

cv2.destroyAllWindows()

虽然变模糊了，但是效果感觉并不是很好呀？这个是因为滤波器的局限性。有此我们引出了腐蚀膨胀的概念，我们可以通过开运算来去毛刺，闭运算去噪，先开后闭两个都用来更好的去除噪声。本来这节课想讲腐蚀膨胀，可是篇幅太长，下节课再讲吧。

———————————————

如果对我的课程感兴趣的话，欢迎关注小木希望学园-微信公众号： 

mutianwei521

也可以扫描二维码哦！