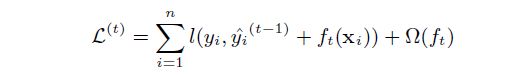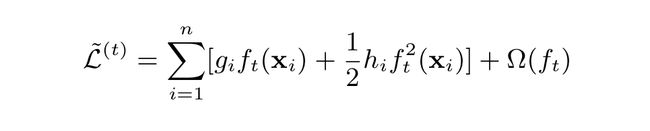超详细解释XGBoost,一篇文章搞懂XGBoost
XGBoost
文章目录
- XGBoost
- 背景
- 工程原理
-
- 具体形式
- 怎么做出预测
- 目标函数
-
- 引言
- 数学详解
-
- 明确符号
- 化简目标函数
-
- 符号注释
- 结论
- 生成一棵完整的树
-
-
- 贪心算法
- 加权分位法
-
- 工作原理
- 数学原理
- 作用
- 算法描述
- 策略
-
- 全局策略
- 局部策略
- 两种策略相比
- 总结
- 例子
- 缺失值处理
- shrinkage(收缩率)
-
- 超参数/参数
- References
背景
XGBoost 最初是由 Tianqi Chen 作为分布式(深度)机器学习社区(DMLC)组的一部分的一个研究项目开始的。XGBoost后来成为了Kaggle竞赛传奇——在2015年的時候29个Kaggle冠军队伍中有17队在他们的解决方案中使用了XGboost。人们越来越意识到XGBoost的强大威力。夸张一点说,如果你不会XGboost,那你参加Kaggle竞赛就是去送人头的。
XGboost到底是什么呢?Tianqi Chen在XGboost的论文中写道:”Tree boosting is a highly effective and widely used machine learning method. In this paper, we describe a scalable end-to-end tree boosting system called XGBoost, which is used widely by data scientists to achieve state-of-the-art results on many machine learning challenges.“[1] 总结一下,XGBoost是一个可拓展的Tree boosting算法,被广泛用于数据科学领域。
XGBoost可以说是GBDT(Gradient Boosting Decision Tree)梯度提升树的一个改进版本。XGBoost中的X代表的就是eXtreme(极致),XGBoost能够更快的、更高效率的训练模型。这就是为什么XGBoost可以说似乎GBDT的一个改进版本。正是得益于XGBoost的高效率,使得她成为数据竞赛中的一大杀器。
工程原理
想要了解一个算法,首先得从宏观上知道这个算法是怎么工作的:1、算法的具体形式;2、怎么做出预测
具体形式
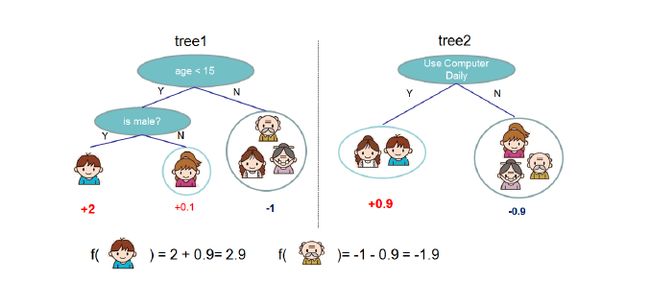
XGboost的可视化(如下图,一个由两棵决策树组成的XGBoost)
重点:
1、XGboost的基本组成元素是:决策树;我们将这些决策树成为”弱学习器“,这些”弱学习器“共同组成了XGboost
2、组成XGBoost的决策树之间是有先后顺序的;后一棵决策树的生成会考虑前一棵决策树的预测结果,即将前一棵决策树的偏差考虑在内(在目标函数中有体现)
3、生成每棵决策树使用的数据集,是整个数据集。所以可以将每棵决策树的生成都看作是一个完整的决策树生成过程
怎么做出预测
一个新样本的预测:新样本依次进入XGBoost的每棵决策树。在第一棵决策树,有一个预测值;在第二棵决策树,有一个预测值,依次类推···直到进入完所有”弱学习器“(决策树)。最后,将“在每一颗决策树中的值”相加,即为最后预测结果。
举例:还是刚刚那张图,样本“儿子”在tree1中的预测值为+2,在tree2中为+0.9。将两个值相加,2+0.9=2.9,所以XGboost最后预测样本“儿子”的值为2.9
目标函数
引言
到这里,我们已经知道了一个XGBoost模型到底是什么工作的了。那XGboost模型到底是怎么生成的呢?XGboost中的“弱学习器”是怎么生成的?
了解机器学习的都知道,要评价我们产生的模型是否是最好的,其依据是“目标函数”。目标函数越小,这个模型才越是我们想要的。刚刚提到,XGboost中的“弱学习器”是“决策树”。在经典的“决策树”算法中,ID3的目标函数基于“信息熵”,CART的目标函数基于“GINI系数”。而在XGboost中,“决策树“的目标函数引入了”偏差“这个变量,这也是XGBoost的魅力所在。
总结一下:XGboost的”弱学习器“是”决策树“,每棵”决策树”都是目标函数值最小时的模型。只有这棵“决策树”的目标函数值最小,才会被选为“弱学习器”。
数学详解
要想清楚了解XGBoost的原理,需要对其目标函数进行数学上的解析。这样,我们才能知道,每一个”弱学习器“是怎么生成的。
我们已经知道,要生成一棵好的决策树,目标是:是其目标函数值最小。那问题是,我们该如何使得其最小呢?其中,涉及到两个问题:
问题1:怎么设置叶子节点的值?
问题2:如何进行结点的分裂(怎么构造树的结构)?
围绕问题1问题,笔者对目标函数进行了手写的数学详解
第t个决策树的目标函数公式如下
明确符号
1、 l ( y i , y ^ i ( t − 1 ) ) l({y}_{i},\widehat{y}_{i}^{(t-1)}) l(yi,y i(t−1)) 表示与 y i , y ^ i ( t − 1 ) {y}_{i},\widehat{y}_{i}^{(t-1)} yi,y i(t−1) 有关的损失函数,这个损失函数是可以根据需要自己定义的
2、 y ^ i ( t − 1 ) \widehat{y}_{i}^{(t-1)} y i(t−1) 表示”前t-1棵决策树“对样本i的预测值(将前t-1棵决策树中的每棵决策树的预测值相加所得); y i {y}_{i} yi 表示样本i的实际值
3、 f t ( x i ) f_{t}(x_{i}) ft(xi) 表示”第t棵决策树“对样本i 的预测值
4、 Ω ( f t ) \Omega(f_{t}) Ω(ft) 表示第t棵树的模型复杂度
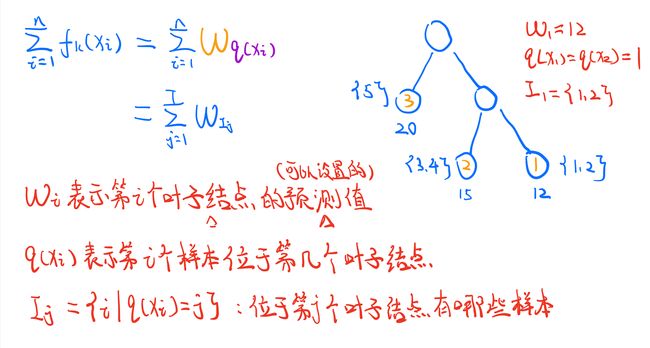
所以,我们有结论如下图:总共k棵树对样本i的预测值=前k-1棵预测树的预测值+第k棵树的预测值
化简目标函数
1、将刚刚得到的: y ^ i ( k ) = y ^ i ( k − 1 ) + f k ( x i ) \widehat{y}_{i}^{(k)}=\widehat{y}_{i}^{(k-1)}+{f}_{k}(x_{i}) y i(k)=y i(k−1)+fk(xi) 替换进目标函数。过程如下图
2、紧接着第一步的结果,我们有以下目标——怎么样才能使目标函数最小(如下图)
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-E8rsrcaA-1662714938255)(https://typora-nigel.oss-cn-nanjing.aliyuncs.com/img/未命名图片.png)]
3、为了解决这个问题,我们对目标函数进行化简。根据数学知识,我们可以使用“泰勒展开”对一个函数进行化简。具体过程如下图
大致的思路:1、使用泰勒展开;2、将常数项忽略(因为我们的目标是找最小值);3、转换一些符号,使式子更简洁
注释
Ω ( f k ) = γ T + 1 2 λ ∑ j = 1 T w j 2 \Omega(f_{k})=\gamma T + \frac{1}{2} \lambda\sum_{j=1}^T w_{j}^2 Ω(fk)=γT+21λj=1∑Twj2
符号注释
1、$ W_{i} $ 表示该树中,第i个叶子结点的值
2、$ q(x_{i}) $ 表示第i个样本位于第几个叶子结点
3、 I j I_{j} Ij 表示位于第j个叶子结点有哪些样本
4、$ G_{j}$ 表示所有属于第j个叶子结点的样本的 g i g_{i} gi 总和,$ H_{j}$ 表示所有属于第j个叶子结点的样本的 h i h_{i} hi 总和
4、 T T T 表示叶子结点数量
例子:
结论
通过上面目标函数的化简,可以回答一开始提出的问题一了
1、应该怎么设置叶子结点的值?
答:应该将叶子结点的值 W j W_{j} Wj 设为 − G j H j + λ \frac{-G_{j}}{H_{j}+\lambda} Hj+λ−Gj ,此时该树的目标函数最小
2、目标函数化简后提高了什么信息?
答:叶子结点的值和目标函数的大小,与“前k-1个决策树”的偏差有关。且每个决策树在结构确定的前提下,目标函数最小为 − 1 2 ∑ j = 1 T G j H j + λ + γ T -\frac{1}{2}\sum_{j=1}^T \frac{G_{j}}{H_{j}+\lambda}+\gamma T −21∑j=1THj+λGj+γT ,人话就是:先求每个叶子结点中的样本的偏差的一次导数和二次导数相除,再对所有叶子节点求和
例子:还是这个例子,但是这里的Obj表示的不是目标函数最小的时候,所以应该改一下,在前面乘 1 2 \frac{1}{2} 21 (笔者这里没在图中修改)
生成一棵完整的树
到这里,我们已经知道,怎么样设置叶子节点的值,可以使得该树的目标函数最小了,之后我们就可以选择目标函数值最小的决策树,作为XGBoost的一个“弱学习器”。但在实际应用中有一个问题:我们无法做到遍历所有的树形结构,也就是说我们不能通过计算所有树形结构的目标函数值,而实现选出其中最小那个。因此下面要解决的问题是:怎样高效的产生一棵决策树呢?
主要内容
贪心算法
与传统的决策树生成方法类似,在XGBoost中,我们也可以利用贪心算法生成一棵树,着将大大的提高效率。
贪心算法,简单来说,就是保证每一步都是最优解,从而达到全局最优解的方法。放到决策树的生成中,就是:保证每一次结点的分裂产生的新的树,都是目标函数值最小的。
举例:如下图,假设现在有四个特征,我们要构造决策树的第一层。第一步:分别将每个特征都依次作为第一层结点;第二步:计算相应的目标函数值;第三步:比较哪个最小,选取最小的作为结果。
下图的例子中,因为选取特征D为第一层的决策树,目标函数最小,所以结果为红色部分。
那如何判断是否应该分裂这个节点呢?
与传统决策树的判断依据一样——增益。只有当将这个结点分裂后,形成的新的树的目标函数值比之前的小,才分裂。换句话说,就是分裂后的树一定要比分裂前的树,目标函数更小。计算方式如下图。
解释:如果当前结点A要分裂成B和C,原先A结点的目标函数值,减去B和C部分的目标函数值的和。如果大于0,则代表分裂有益,可以分裂。
注意:这里有一个惩罚项 γ \gamma γ ,表示有时候增益太小的话,相比于增加模型复杂度的副作用,不选择进行分裂
第二层、第三层、重复上述步骤,直到整个决策树所有特征都被使用,或者已经达到限定的层数。
算法描述如下
加权分位法
我们刚刚利用贪心算法解决了"如何高效的产生一棵决策树"的问题,但其实这个问题还没有完全解决。不知道你有没有注意到,在刚刚举的例子中,并没有给出每个特征具体的划分。例如,上个例子的图中,决策树D,并没有给出例如"D<5"这样的划分,仅仅只是说根据特征D来进行划分。
我们假设,特征D是一个离散的连续变量,有10个不同的值,范围是[1,10]。那么如果选择特征D时,需要尝试10中不同的划分,从D≤1到D≤9.这是一个非常繁琐的步骤,会导致算法的效率很低。那么XGBoost又是怎么解决这个问题的呢?有没有一种办法,可以不用尝试每一种的划分,只选取几个值进行尝试?为了解决这个问题,XGBoost中用了一个全新的方法:加权分位法
工作原理
为了得到值得进行尝试的划分点,我们需要一个函数对该特征的特征值进行"重要性"排序。根据排序的结果,再选出值得进行尝试的特征值。
数学原理
我们来看一下,我们化简得到的目标函数(如下)
对目标函数进行数学变换,结果如下。可以发现,目标函数是一个:真实值为 $\frac{g_{i}}{h_{i}} $ ,权重为 h i h_{i} hi的平方损失。因此,我们可以得出结论:一个样本对于目标函数值的贡献,在于其得到的 h i h_{i} hi。
这样我们可以根据 h i h_{i} hi对特征值的"重要性"进行排序。到这,XGBoost提出了一个新的函数,这个函数用于表示一个特征值的"重要性"排名,如下图
我们来解释一下这个函数:
1、 D k D_{k} Dk 解释如下:第k个特征的每个样本的特征值( x n k x_{nk} xnk)与其相应的 h i h_{i} hi组成的集合。 ( x 1 k , h 1 ) (x_{1k},h_{1}) (x1k,h1) 表示第一个样本对于第k个特征的特征值,和其对应的 h i h_{i} hi
D k = { ( x 1 k , h 1 ) , ( x 2 k , h 2 ) . . . ( x n k , h n ) } D_{k}= \set{(x_{1k},h_{1}),(x_{2k},h_{2})...(x_{nk},h_{n})} Dk={(x1k,h1),(x2k,h2)...(xnk,hn)}
2、 r k ( z ) r_{k}(z) rk(z) 的分母表示为:第k个特征的所有样本的 h i h_{i} hi 总和;分子:所有特征值小于z的样本的 h i h_{i} hi 总和
3、注意,这里是 x < z x
之后对一个特征的所有特征值进行排序。在排序之后,设置一个值 ϵ \epsilon ϵ 。这个值用于对要划分的点进行规范,满足要求如下:对于特征k的特征值的划分点 { s k 1 , s k 2 . . . s k l } \set {s_{k1},s_{k2}...s_{kl}} {sk1,sk2...skl} 有,两个相连划分点的 r k r_{k} rk 值的差的绝对值要小于 ϵ \epsilon ϵ 。同时,为了增大算法的效率,也可以选择每个切分点包含的特征值数量尽可能多。人话就是,根据特征值的 r k r_{k} rk 进行排序后,大约要选出 1 / ϵ 1/\epsilon 1/ϵ 个的点作为切分点。
∣ r k ( s k , j ) − r k ( s k , j + 1 ) ∣ < ϵ |r_{k}(s_{k,j})-r_{k}(s_{k,j+1})|<\epsilon ∣rk(sk,j)−rk(sk,j+1)∣<ϵ
例子:
假设对一个特征有:特征值1到4,其 h i h_{i} hi , r k r_{k} rk 如下, ϵ = 0.5 \epsilon=0.5 ϵ=0.5 。如果我们的策略是切分点尽可能少,那么我们得到的切分点应该是{2,3}:x<2,x<3。因为: r k ( 2 ) = 0.4 < 0.5 r_{k}(2)=0.4<0.5 rk(2)=0.4<0.5 但 r k ( 3 ) = 0.7 > 0.5 r_{k}(3)=0.7>0.5 rk(3)=0.7>0.5 ;之后, ∣ r k ( 2 ) − r k ( 3 ) ∣ = 0.3 < 0.5 |r_{k}(2)-r_{k}(3)|=0.3<0.5 ∣rk(2)−rk(3)∣=0.3<0.5 但 ∣ r k ( 2 ) − r k ( 4 ) ∣ = 0.5 |r_{k}(2)-r_{k}(4)|=0.5 ∣rk(2)−rk(4)∣=0.5 。所有切分点是:{2,3}。
| 特征值 | h i h_{i} hi | r k r_{k} rk |
|---|---|---|
| 1 | 4 | r k ( 1 ) = 0 r_{k}(1)=0 rk(1)=0 |
| 2 | 3 | r k ( 2 ) = 0.4 r_{k}(2)=0.4 rk(2)=0.4 |
| 3 | 2 | r k ( 3 ) = 0.7 r_{k}(3)=0.7 rk(3)=0.7 |
| 4 | 1 | r k ( 4 ) = 0.9 r_{k}(4)=0.9 rk(4)=0.9 |
作用
在我们得到了使用加权分位法的分裂点之后,在贪心算法的分裂过程中,我们就只需要对这几个分裂点进行尝试,而不需要与原先一样,对所有的特征值进行尝试。这大大减少了算法的开销。
算法描述
策略
基于加权分位法,我们有两种策略进行分裂点的计算:1、全局策略;2、局部策略
全局策略
顾名思义,全局策略,我们在一棵树的生成之前,就已经计算好每个特征的分裂点。并且在整个树的生成过程当中,用的都是一开始计算的分裂点。这也就代表了,使用全局策略的开销更低,但如果分裂点不够多的话,准确率是不够高的
局部策略
局部策略,对每一个结点所包含的样本,重新计算其所有特征的分裂点。我们知道,在一棵树的分裂的时候,样本会逐渐被划分到不同的结点中,也就是说,每个结点所包含的样本,以及这些样本有的特征值是不一样的。因此,我们可以对每个结点重新计算分裂点,以保证准确性,相当于是因地制宜的方法。这也就代表了,使用局部策略的开销更大,但分裂点数目不用太多,也能够达到一定的准确率。
两种策略相比
根据上图,我们可以得出结论:
1、在分裂点数目相同,即eps( ϵ \epsilon ϵ )相同的时候,全局策略的效果 < 局部策略
2、分裂点数目越多,两个策略的效果都越好
3、全局策略可以通过增加分裂点数目,达到逼近局部策略的效果
总结
至此,我们已经知道了一棵完整的树是怎么生成的了。
步骤
1、基于贪心算法进行划分,通过计算目标函数增益,选择该结点使用哪个特征
2、为了提高算法效率,使用“加权分位法”,计算分裂点。只考虑计算分裂点的目标函数值,而不是考虑所有特征值
3、可以选择“全局策略”还是“局部策略”计算分裂点
例子
下图是笔者在kaggle Titanic比赛时候训练的XGBoost的其中一棵决策树。其中,笔者选择的是全局策略进行计算。在下图中可以看到一个值得注意的地方:并不是一个特征在使用了一次后就不会再使用了,而是一个分裂点被使用后,这个分裂点包含的所有情况就不会再被使用了。例如,图中的FS特征,在第二层和第三层都有被使用
缺失值处理
从上面的例子,我们可以看到有一条蓝色的线,上面写着“yes,missing”,这表示只要是缺失值就跟着蓝色线走。这是XGBoost对缺失值的处理方法。那这个蓝色的线又是如何生成的呢?生成的算法如下图
这个算法实际上做的是一件非常简单的事情。对于第k个特征,我们首先将样本中第k个特征的特征值为缺失值的样本全部剔除。然后我们正常进行样本划分。最后,我们做两个假设,一个是缺失值全部摆左子结点,一个是摆右子节点。哪一个得到的增益大,就代表这个特征最好的划分。总结一下,就是缺失值都摆一起,选最好的情况
注意:对于加权分位法中对于特征值的排序,缺失值不参与。也就是说缺失值不会作为分裂点。gblinear将缺失值视为0。
shrinkage(收缩率)
shrinkage(收缩率)是一个对于“弱学习器”的权重值。shrinkage的目的是防止过拟合,具体公式如下。解释一下,就是对每个“弱学习器”的预测值乘 η \eta η ,来缩小预测值( 0 < η < = 1 0<\eta<=1 0<η<=1) ,达到防止过拟合的效果。
y ^ i t = y ^ i ( t − 1 ) + η f t ( x i ) \widehat y_{i}^{t}=\widehat y_{i}^{(t-1)}+\eta f_{t}(x_{i}) y it=y i(t−1)+ηft(xi)
超参数/参数
超参数的训练是模型训练中至关重要的一环。对于一个不变的数据集,超参数的设置决定了模型的效果。下面就来总结一下XGBoost中的超参数以及每个超参数的影响。
注意:下列表格中列出的超参数/参数的名称,会因为调用的包不同而有不一样的名称。表格的超参数以python中的XGBoost为准(网页链接)
| 超参数 | 取值 | 影响 |
|---|---|---|
| objective | 常用:reg:logistic,binary:logistic,binary:logitraw,multi:softmax | 根据你的目标进行选择,得到不同的结果,以及损失函数会不一样 |
| n_estimators(sklearn-API),num_round | ( 0 , ∞ ] (0,\infty] (0,∞] | ”弱学习器“的数量 |
| base_score | default=0.5 | 所有实例的初始预测分数,如果”弱学习器“足够多,不会有影响 |
| eval_metric | rmse,rmsle,mae,mape,mphe,logloss,error,error@t,merror,mlogloss,auc,aucpr··· | 验证数据的评估指标 |
| eta(learning_rate) | [0,1] | shrinkage中的 η \eta η ,对每个学习器的权重;越小,越减少过拟合 |
| gamma | [ 0 , ∞ ] [0,\infty] [0,∞] | 当一个结点的分裂,目标函数的增益大于“gamma”才进行分裂;是一个模型复杂度惩罚项,越大,越不分裂 |
| max_depth | [ 0 , ∞ ] [0,\infty] [0,∞] | 树的最大深度,0表示没有限制 |
| min_child_weight | [ 0 , ∞ ] [0,\infty] [0,∞] | 结点样本的 h i h_{i} hi(偏差的二次导数)的和的最小值,也就是说如果结点的 h i h_{i} hi 小于设定的值,就不分裂了。在线性回归中,可以理解为结点的样本数。越大,越不分裂 |
| max_delta_step | [ 0 , ∞ ] [0,\infty] [0,∞] | 允许每个叶子输出的最大增量步长,适用于样本极度不平衡的时候。通常为0,表示不受限制。并且这个超参数通常不用。但当类极度不平衡时,它可能有助于逻辑回归。将其设置为 1-10 的值可能有助于控制模型。 |
| subsample | ( 0 , 1 ] (0,1] (0,1] | 选择多少百分比的样本进行训练,每次训练一棵新的树,都会进行重新采样。用于防止过拟合;原理:基于部分数据产生的一棵新的树,都会作用在整个数据集上进行预测,这样可以得到所有样本的偏差,然后下一棵树在重新抽样 |
| sampling_method | uniform,gradient_based | uniform:每个训练实例被选中的概率相等。通常设置 subsample>= 0.5 以获得良好的结果;gradient_based:每个训练实例的选择概率与梯度的正则化绝对值成正比 。这时可以subsample可以设置低到0.1也不会影响模型精度。只有当"tree_method"为”gpu_hist"才可以用这个方法,其他都只能用“uniform” |
| colsample_bytree colsample_bylevel colsample_bynode |
( 0 , 1 ] (0,1] (0,1],default=1 | 对特征进行采样的方法。分步骤进行:1、colsample_bytree:采样一棵树能运用的特征;2、colsample_bylevel:对colsample_bytree后的结果,再次进行抽样,得到对一棵树某一层的结点能用的特征;3、colsample_bynode:基于colsample_bylevel的结果,进行抽样,得到这一层的这一个结点能用的特征。 所以,如果{‘colsample_bytree’:0.5, ‘colsample_bylevel’:0.5, ‘colsample_bynode’:0.5},总共有64个特征,表示:1、每棵树只能用0.5的特征数,等于32;2、在0.5的特征数基础上,再取0.5的特征作为这一层的可选特征,等于16;3、在某一层可选特征中,再选0.5作为这个结点的可选特征,等于8。 |
| lambda | [ 0 , ∞ ] [0,\infty] [0,∞],default=1 | 权重(叶子结点的预测值)的L2正则化参数;可以理解为:越大,目标函数越大 |
| alpha | [ 0 , ∞ ] [0,\infty] [0,∞],default=0 | 权重(叶子结点的预测值)的L1正则化参数;可以理解为:越大,目标函数越大 |
| sketch_eps | ( 0 , 1 ] (0,1] (0,1],default=0.3 | 仅用于“updater=grow_local_histmaker”。用于精确控制分箱的数量(类似于 ϵ \epsilon ϵ ) |
| scale_pos_weight | ( 0 , ∞ ] (0,\infty] (0,∞],default=1 | 控制正负样本不平衡的情况,一般考虑值为"sum(negative instances) / sum(positive instances)" |
| max_leaves | [ 0 , ∞ ] [0,\infty] [0,∞],default=0 | 最大叶子结点的数量,“tree_method=exact"不可用 |
| max_bin | [ 0 , ∞ ] [0,\infty] [0,∞],default=256 | 最大分箱数(其实就是分裂点的数目),“tree_method=hist,approx,gpu_hist"时可用 |
| num_parallel_tree | [ 0 , ∞ ] [0,\infty] [0,∞],default=1 | 每次迭代并行生成多少棵树,仅支持”boosted random forest“ |
| 参数 | 取值 | 影响 |
|---|---|---|
| booster | gbtree,gblinear,dart | XGBoost中的“弱学习器”的模型类型:树还是线性 |
| verbosity | 0,1,2,3 | 训练的时候要显示什么信息,数字越大,显示信息越详细 |
| nthread | int | 选择线程数 |
| disable_default_eval_metric | 0,1 | 是否禁用默认的指标,0为false,1为True |
| tree_method | auto,exact,approx,hist,gpu_hist, | exact:精确贪心算法 approx:使用分位数草图和梯度直方图的近似贪心算法(就是加权分类法),是全局策略的 hist:更快的直方图优化近似贪心算法,使用的是用户提高的权重,而不是 h i h_{i} hi,全局策略 gpu_hist:基于GPU实现hist auto:根据数据集大小,自动选择方法;小数据集,使用exact;较大数据集,使用approx;大数据集,使用hist或者gpu_hist |
| updater | grow_local_histmaker,prune,refresh,sync | 要使用这个参数,得设置参数“process——type”:{“process_type”: “update”, “updater”: “[grow_local_histmaker,prune,refresh,sync]”} grow_local_histmaker:近似算法,局部策略(很少使用) |
| refresh_leaf | 0,1 | 当“updater=refresh”可用,refresh_leaf=1,更新树叶和树结点的统计信息;refresh_leaf=0,仅更新结点的统计信息 |
| process_type | default,update | default表示用正常的去生成树,update表示用"updater"中的参数方法 |
| grow_policy | depthwise(default),lossguide | 当“tree_method=[hist,approx,gpu_hist]”时可用。 depthwise:倾向于在离根结点近的地方进行分裂(深度优先,保证平衡) lossguide:倾向于在目标函数变化最大的结点处分裂(可能会使树不平衡) |
| predictor | auto,cpu_predictor,gpu_predictor | auto:自动选择。如果”tree_method=gpu_hist“,提供基于GPU的预测,而无需复制所有数据到GPU内存 cpu_predictor:多核cpu预测 gpu_predictor:当”tree_method=gpu_hist“时可用。将所有数据复制到GPU中进行预测 |
| monotone_constraints | 变量单调性的约束,有关详细信息,请参阅单调约束。 | |
| interaction_constraints | 表示允许交互的交互约束。约束必须以嵌套列表的形式指定,例如,其中每个内部列表是一组允许相互交互的特征索引。[[0, 1], [2, 3, 4]]`,有关详细信息,请参阅特征交互约束。 | |
| seed | random | 随机数种子 |
Tree_mehtod & updater
| Exact | Approx | Hist | GPU Hist | |
|---|---|---|---|---|
| grow_policy | Depthwise | depthwise/lossguide | depthwise/lossguide | depthwise/lossguide |
| max_leaves | F | T | T | T |
| sampling method | uniform | uniform | uniform | gradient_based/uniform |
| categorical data | F | T | T | T |
| External memory | F | T | T | P(部分支持) |
| Distributed(分布式) | F | T | T | T |
References
[1] Tianqi Chen,Carlos Guestrin. XGBoost: A Scalable Tree Boosting System.