【论文简介】Stable Diffusion的基础论文:High-Resolution Image Synthesis with Latent Diffusion Models

稳定扩散生成模型(Stable Diffusion)是一种潜在的文本到图像扩散模型，能够在给定任何文本输入的情况下生成照片般逼真的图像
Stable Diffusion 是基于latent-diffusion 并与 Stability AI and Runway合作实现的

• paper: High-Resolution Image Synthesis with Latent Diffusion Models
• 模型下载与社区：https://huggingface.co/CompVis/stable-diffusion |
• 在线试用demo
• 原始代码：https://github.com/CompVis/latent-diffusion
• 工程优化后的项目：https://github.com/CompVis/stable-diffusion

图5 基于提出的LDM模型的文本到图像合成示例。

模型是在LAION 数据集上训练的。使用200个DDIM迭代和η = 1.0生成的样本。我们使用无条件指导[32]与s = 10.0。

一、论文概述

摘要

通过将图像结构过程处理为（ decomposing the image formation process）去噪自编码器的连续应用（a sequential application of denoising autoencoders），扩散模型（DMs），实现了对图像数据的最先进的合成结果。
此外，他们的公式（formulation）允许一个指导机制（a guiding mechanism）来控制图像生成过程，而无需再训练.

然而，由于这些模型通常直接在像素空间中运行，强大的DMs模型的优化通常需要数百天的GPU，而且由于顺序评估，推理是昂贵的。

为了了使DM能够在有限的计算资源上进行训练，同时保持其质量和灵活性，我们将其应用于强大的预训练自动编码器（autoencoders）的潜在空间中。

与之前的工作相比，在这种表示上训练扩散模型首次允许在降低复杂度和保持细节复杂度之间达到一个接近最优的点(near-optimal)，大大提高了视觉保真度.。。。

. 通过在模型架构中引入交叉注意层(cross-attention layer)，我们将扩散模型转化为强大而灵活的生成器，用于一般条件输入，如文本或边界框，以卷积方式和高分辨率的合成成为可能。

我们的潜在扩散模型（LDMs）在图像内绘制和类条件图像合成方面获得，并且在各种任务上具有高度竞争力的性能，包括文本到图像合成、无条件图像生成和超分辨率，同时与基于像素的DMs(pixed-based DMS)相比，显著降低了计算需求。

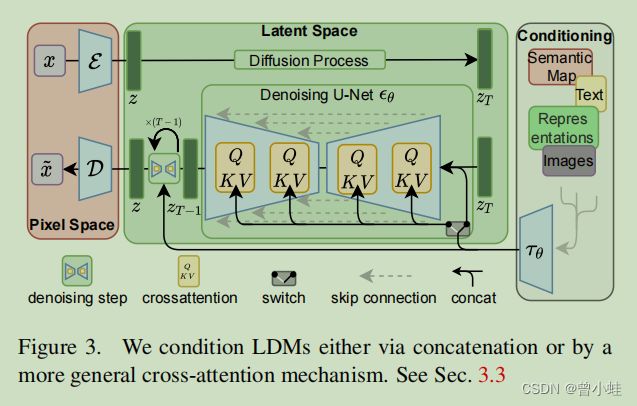
图3，网络结构。

通过连接和更一般的交叉注意力机制，来调节条件 LDMs

图4 特定类数据集训练合成结构

图8 基于coco目标检测框引导合成

图10 超分结果

图11 图像修复结果

1引言

图像合成需要巨大的计算资源。特别是复杂的、自然的场景的高分辨率图像合成，
目前主要是通过扩大基于可能性的（likelihood-based）模型，可能包含自回归（AR）transformers 的数十亿个参数,相关论文为：

• 2102.DALL-E Zero-Shot Text-to-Image Generation （被引：800）
• 1906.VQ-VAE-2 Generating diverse high-fidelity images with VQ-VAE-2

相比之下，GANs的有希望的结果已被揭示大多局限于可变性相对有限的数据 (limited variability)，因为它们的对抗性学习过程不容易扩展(not easyily scale to)到建模复杂的、多模态分布（multi-modal distributions）,相关研究

• 1809.BigGAN:Large scale GAN training for high fidelity natural image synthesis . (DeepMind)（被引 3448）
• 1406.Generative adversarial networks (GAN的开山之作) （被引51091）
• StyleGAN1：A style-based generator architecture for generative adversarial networks. （被引 5146）

最近，扩散模型[82]，基于自动编码器去噪层次，已经显示了令人印象深刻的成就

• [82] 1503.Deep unsupervised learning using nonequilibrium thermodynamics （深度非监督学习使用非平衡热力学方法）（被引450）

结果在图像合成[30,85]和超过并定义了[7,45,48,57]，

• [30] 2006.Denoising diffusion probabilistic models 去噪扩散概率模型 (被引 623)
• [85] 2011.Score based generative modeling through stochastic differential equations. (通过使用随机微分方程进行的基于分数的生成建模。) ( 被引356)
• [7] 2109.Wavegrad: Estimating gradients for waveform generation. （估计波形产生的梯度）.（没有图像生成）(被引193)
• [45] 2107.Variational diffusion models. 变分扩散模型。(被引107)
• [48] A versatile diffusion model for audio synthesis 一种用于音频合成的通用扩散模型 (被引200)
• [57] Symbolic music generation with diffusion models.具有扩散模型的符号性音乐生成。

最先进的类条件图像合成[15,31]和超分辨率[72]。

• [15] 2105.Diffusion models beat gans on image synthesis 扩散模型在图像合成上超过了GANS （openAI） (被引354 )
• [72] 2104.Image super-resolution via iterative refinement 通过迭代细化得到的图像超分辨率 (被引115)

此外，即使是无条件的 DMs，也可以很容易地应用于诸如图像修复和上色等任务[85]

• [85] 2011.Score based generative modeling through stochastic differential equations. (通过使用随机微分方程进行的基于分数的生成建模。) ( 被引356)

基于冲程的(strike-base)合成[53]

• SDEdit: Guided Image Synthesis and Editing with Stochastic Differential Equations

二、需要理解概念

DDIM采样

来自论文 [84] 2010.Denoising diffusion implicit models ( 去噪扩散隐式模型 )

• 去噪扩散概率模型（DDPMs: Denoising diffusion probabilistic model）在没有对抗性训练(without adversarial training)的情况下实现了高质量的图像生成，但它们需要多次模拟马尔可夫链(Markov chain)才能生成样本。
• 为了加速采样，本文提出了去噪扩散隐式模型（DDIMs），这是一种更有效的迭代隐式概率模型（ denoising diffusion implicit models），具有与DDPMs相同的训练过程。一类更有效的迭代隐式概率模型（iterative implicit probabilistic models ），具有与DDPM相同的训练过程。
• DDPMs中，生成过程(generative process)被定义为一个特定的马尔可夫扩散过程的反向过程(as the reverse of a particular Markovian diffusion process)。
• 我们通过一类非马尔可夫扩散过程来推广DDPMs，从而得到相同的训练目标。这些非马尔可夫过程可以对应于确定性的生成过程，从而产生能够快速产生高质量样本的隐式模型。
• 我们的经验（empirically）证明，与DDPMs相比，DDIMs可以快速产生10×到50×的高质量样本，允许我们在样本质量上权衡计算，直接在潜在空间中执行有语义意义的图像插值，并以非常低的误差重建观测（reconstruct observations）

什么是图像生成的扩散模型?（DMs）

• [30] 2006.Denoising diffusion probabilistic models 去噪扩散概率模型 (被引 623)

我们使用扩散概率模型（diffusion probabilistic models）提出了高质量的图像合成结果，这是一类潜在变量模型(a class of latent variable models) 的灵感来自于非平衡热力学的方法（1503.Deep unsupervised learning using nonequilibrium thermodynamics）

最好的结果是根据扩散概率模型的新颖的连接和去噪分数匹配朗之万动力学（ Langevin dynamics）来训练加权变分界（ on a weighted variational bound），和我们的模型自然承认一个渐进的有损减压方案（progressive lossy decompression scheme），可以解释为自回归解码的泛化（as a generalization of autoregressive decoding）。

扩散概率模型(A diffusion probabilistic model)
（为了简洁起见，我们称之为“扩散模型”）
是一个参数化的马尔可夫链，使用变分推理（variational inference）训练，在有限时间后产生与数据匹配的样本，这条链的转换被学习来逆转一个扩散过程，这是一个马尔可夫链，它逐渐在相反的采样方向的数据中增加噪声，直到信号被破坏。。 .当扩散包含少量的高斯噪声时，将采样链转换设置为条件高斯噪声就足够了，允许一个特别简单的神经网络参数化。
扩散模型定义起来很简单， 训练效率也很高。。
我们还证明了扩散模型的一定参数化揭示了训练过程中多个噪声水平的去噪分数匹配(denoising score matching)和采样过程中退火朗之万动力学的等价性（equivalence）