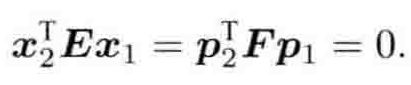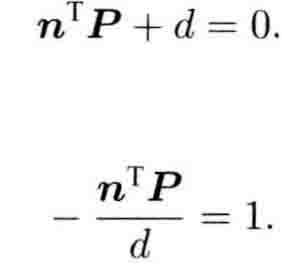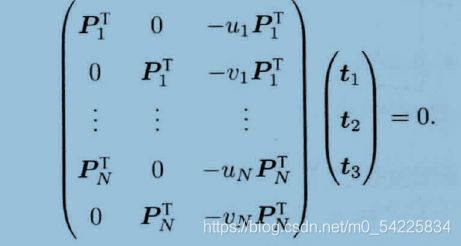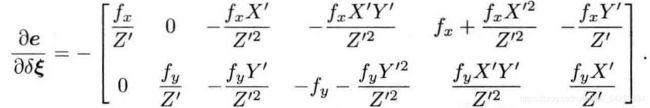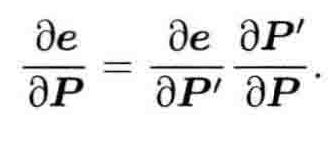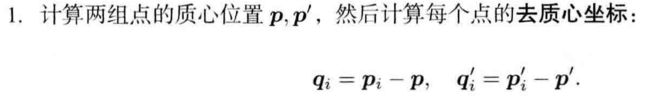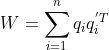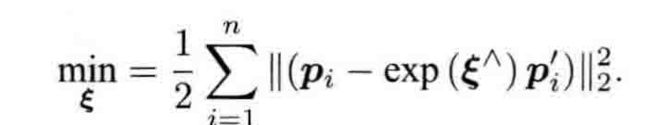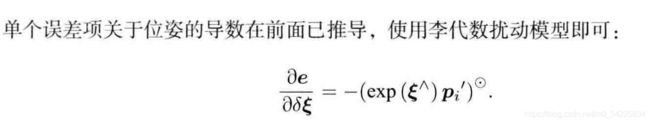SLAM~CH7

本章应掌握知识点：

目录

特征点法

特征点

 ORB特征的提取

FAST关键点

BRIEF描述子

 特征匹配

实践部分

OpenCV的ORB特征

将计算描述子和匹配的过程具象化

对极几何：根据2D-2D点估计运动

对极约束

计算方法

1. 计算E：八点法

 2. SVD分解来计算t，R

 单应矩阵：特征点都落在同一平面

2D-2D得到空间点~三角测量

理论

代码

3D-2D的PnP问题

线性解法

 P3P：利用三角关系

BA法(最小重影误差)求PnP

理论

代码

3D-3D的ICP

SVD方法

非线性优化方法

---

特征点法

特征点

存在意义：视觉里程计的核心问题是如何根据图像估计运动。因此可以找到图像中在相机运动之后仍保持稳定的特征点。

有多种特征点：自然的角点，人工设计的ORB、SIFT、SUFT等等

特征点由关键点和描述子构成

|-关键点：特征点图像中的位置、朝向、大小                                                               

|-描述子：通常是一个向量，描述关键点周围像素的信息。“外观相似的特征由相似的描述子”

 ORB特征的提取

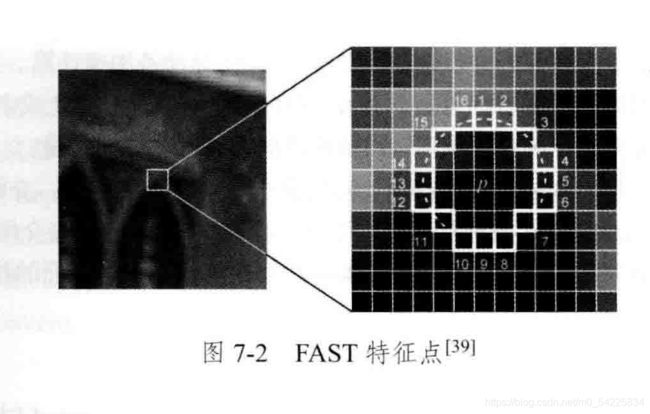
FAST关键点

 

 

   1.   定义矩阵的距为

BRIEF描述子

 特征匹配

这是关键的一步，即确定当前看到的路标与之前看到的路标的关系。

主要介绍暴力匹配法brute-force Matcher

描述子之间的距离表示两个特征的相似程度

1. 先取第一个图像的特征点的一个描述子与第二个图像的所有描述子的距离。

        这里提出Hamming distance: 描述子不同位数的个数 （一般是用这个距离）

2. 排序并取最小。

3. 取第一个图像的特征点的第2个描述子重复以上步骤（两个for循环）

实践部分

OpenCV的ORB特征

#include 
#include 
#include 
#include 
#include 

using namespace std;
using namespace cv;

int main(int argc, char **argv) {
  if (argc != 3) {
    cout << "usage: feature_extraction img1 img2" << endl;
    return 1;
  }
  //-- 读取图像
  Mat img_1 = imread(argv[1], CV_LOAD_IMAGE_COLOR);
  Mat img_2 = imread(argv[2], CV_LOAD_IMAGE_COLOR);
  assert(img_1.data != nullptr && img_2.data != nullptr);

  //-- 初始化
  std::vector keypoints_1, keypoints_2; //关键点
  Mat descriptors_1, descriptors_2;               //描述子
  Ptr detector = ORB::create();  //特征点查找
  Ptr descriptor = ORB::create();//描述子提取器
  Ptr matcher = DescriptorMatcher::create("BruteForce-Hamming");//描述者匹配，使用hamming距离

  //-- 第一步:检测 Oriented FAST 角点位置
  chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
  detector->detect(img_1, keypoints_1);
  detector->detect(img_2, keypoints_2);

  //-- 第二步:根据角点位置计算 BRIEF 描述子
  descriptor->compute(img_1, keypoints_1, descriptors_1);
  descriptor->compute(img_2, keypoints_2, descriptors_2);
  chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
  chrono::duration time_used = chrono::duration_cast>(t2 - t1);
  cout << "extract ORB cost = " << time_used.count() << " seconds. " << endl;

  Mat outimg1;
  drawKeypoints(img_1, keypoints_1, outimg1, Scalar::all(-1), DrawMatchesFlags::DEFAULT);
  imshow("ORB features", outimg1);//显示

  //-- 第三步:对两幅图像中的BRIEF描述子进行匹配，使用 Hamming 距离
  vector matches;
  t1 = chrono::steady_clock::now();
  matcher->match(descriptors_1, descriptors_2, matches);
  t2 = chrono::steady_clock::now();
  time_used = chrono::duration_cast>(t2 - t1);
  cout << "match ORB cost = " << time_used.count() << " seconds. " << endl;

  //-- 第四步:匹配点对筛选
  // 计算最小距离和最大距离
  auto min_max = minmax_element(matches.begin(), matches.end(),
                                [](const DMatch &m1, const DMatch &m2) { return m1.distance < m2.distance; });
  double min_dist = min_max.first->distance;
  double max_dist = min_max.second->distance;

  printf("-- Max dist : %f \n", max_dist);
  printf("-- Min dist : %f \n", min_dist);

  //当描述子之间的距离大于两倍的最小距离时,即认为匹配有误.但有时候最小距离会非常小,设置一个经验值30作为下限.
  std::vector good_matches;
  for (int i = 0; i < descriptors_1.rows; i++) {
    if (matches[i].distance <= max(2 * min_dist, 30.0)) {
      good_matches.push_back(matches[i]);
    }
  }

  //-- 第五步:绘制匹配结果
  Mat img_match;
  Mat img_goodmatch;
  drawMatches(img_1, keypoints_1, img_2, keypoints_2, matches, img_match);
  drawMatches(img_1, keypoints_1, img_2, keypoints_2, good_matches, img_goodmatch);
  imshow("all matches", img_match);
  imshow("good matches", img_goodmatch);
  waitKey(0);

  return 0;
}

将计算描述子和匹配的过程具象化

计算描述子

void ComputeORB(const cv::Mat &img, vector &keypoints, vector &descriptors) {
  const int half_patch_size = 8;
  const int half_boundary = 16;
  int bad_points = 0;
  for (auto &kp: keypoints) {
    if (kp.pt.x < half_boundary || kp.pt.y < half_boundary ||
        kp.pt.x >= img.cols - half_boundary || kp.pt.y >= img.rows - half_boundary) {
      // outside
      bad_points++;
      descriptors.push_back({});
      continue;
    }

    float m01 = 0, m10 = 0;
    for (int dx = -half_patch_size; dx < half_patch_size; ++dx) {
      for (int dy = -half_patch_size; dy < half_patch_size; ++dy) {
        uchar pixel = img.at(kp.pt.y + dy, kp.pt.x + dx);
        m10 += dx * pixel;
        m01 += dy * pixel;
      }
    }

    // angle should be arc tan(m01/m10);
    float m_sqrt = sqrt(m01 * m01 + m10 * m10) + 1e-18; // avoid divide by zero
    float sin_theta = m01 / m_sqrt;
    float cos_theta = m10 / m_sqrt;

    // compute the angle of this point
    DescType desc(8, 0);
    for (int i = 0; i < 8; i++) {
      uint32_t d = 0;
      for (int k = 0; k < 32; k++) {
        int idx_pq = i * 32 + k;
        cv::Point2f p(ORB_pattern[idx_pq * 4], ORB_pattern[idx_pq * 4 + 1]);
        cv::Point2f q(ORB_pattern[idx_pq * 4 + 2], ORB_pattern[idx_pq * 4 + 3]);

        // rotate with theta
        cv::Point2f pp = cv::Point2f(cos_theta * p.x - sin_theta * p.y, sin_theta * p.x + cos_theta * p.y)
                         + kp.pt;
        cv::Point2f qq = cv::Point2f(cos_theta * q.x - sin_theta * q.y, sin_theta * q.x + cos_theta * q.y)
                         + kp.pt;
        if (img.at(pp.y, pp.x) < img.at(qq.y, qq.x)) {
          d |= 1 << k;
        }
      }
      desc[i] = d;
    }
    descriptors.push_back(desc);
  }

  cout << "bad/total: " << bad_points << "/" << keypoints.size() << endl;
}

特征匹配

* 设定m为最终储存的距离，distance是暂存的距离

 * 计算第一张图片一个特征点与第二张图片所有特征点的距离

 for (int k = 0; k < 8; k++) {
        distance += _mm_popcnt_u32(desc1[i1][k] ^ desc2[i2][k]);
      }

 *排序并取最小

 if (distance < d_max && distance < m.distance) {//排序
        m.distance = distance;
        m.trainIdx = i2;
      }

 *判断是否太大并压入输出数组

 if (m.distance < d_max) {
      matches.push_back(m);
    }

void BfMatch(const vector &desc1, const vector &desc2, vector &matches) {
  const int d_max = 40;

  for (size_t i1 = 0; i1 < desc1.size(); ++i1) {
    if (desc1[i1].empty()) continue;
    cv::DMatch m{i1, 0, 256};                                   //m为
    for (size_t i2 = 0; i2 < desc2.size(); ++i2) {
      if (desc2[i2].empty()) continue;
      int distance = 0;
      for (int k = 0; k < 8; k++) {
        distance += _mm_popcnt_u32(desc1[i1][k] ^ desc2[i2][k]);//向量的hamming distance
      }
      if (distance < d_max && distance < m.distance) {//排序
        m.distance = distance;
        m.trainIdx = i2;
      }
    }
    if (m.distance < d_max) {
      matches.push_back(m);
    }
  }
}

对极几何：根据2D-2D点估计运动

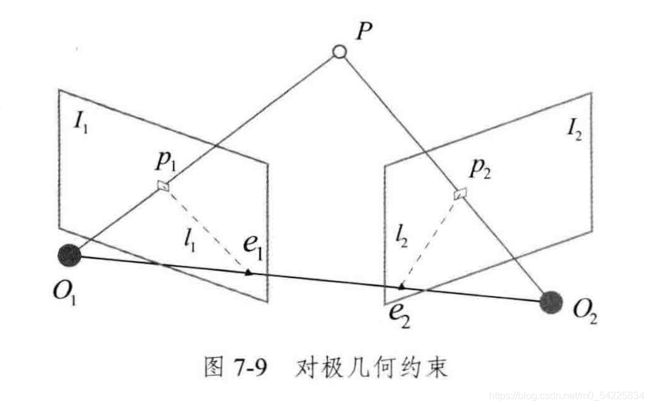
对极约束

 和是极平面，e1、e2是极点，l1和l2是极线，O1O2连线叫基线，p1、p2是p在图像1、2中的特征点

                                                                 

 

记

本质矩阵(Essential)        

基础矩阵(Fundamental) 

 

因此相机的位姿变为：计算E或F，再得到R、t

计算方法

1. 计算E：八点法

 则等式变为求解

 2. SVD分解来计算t，R

先求解出U、、V：奇异值分解（SVD） - 知乎 (zhihu.com)

 

 单应矩阵：特征点都落在同一平面

适合于场景中所有特征点都落在同一平面

 设平面满足

即

得到：（具体过程看书）

 

 求解得到单应矩阵H再SVD分解。

单应矩阵的意义

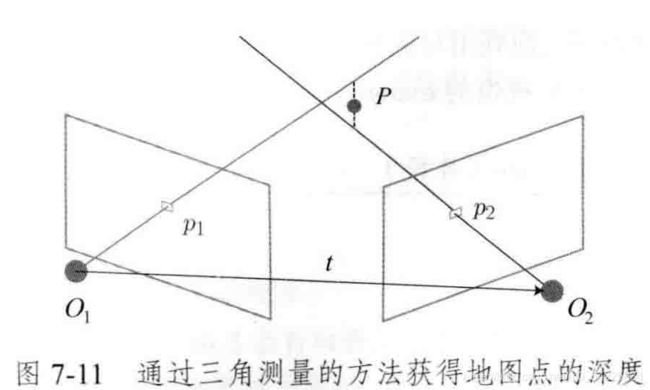
2D-2D得到空间点~三角测量

理论

s_1、s_2为未知量 

 得到式子

                                                        ​​​​​​​        ​

得：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​          

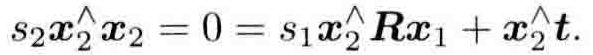
 即可求得s1再由s1得到s2

代码

 1. 变换矩阵用，3X4的表示形式

Mat T1 = (Mat_(3, 4) <<
    1, 0, 0, 0,
    0, 1, 0, 0,
    0, 0, 1, 0);
  Mat T2 = (Mat_(3, 4) <<
    R.at(0, 0), R.at(0, 1), R.at(0, 2), t.at(0, 0),
    R.at(1, 0), R.at(1, 1), R.at(1, 2), t.at(1, 0),
    R.at(2, 0), R.at(2, 1), R.at(2, 2), t.at(2, 0)

2. 三角化

  Mat pts_4d;
  cv::triangulatePoints(T1, T2, pts_1, pts_2, pts_4d);

3. 转换成非齐次坐标

  for (int i = 0; i < pts_4d.cols; i++) {
    Mat x = pts_4d.col(i);
    x /= x.at(3, 0); // 归一化
    Point3d p(
      x.at(0, 0),
      x.at(1, 0),
      x.at(2, 0)
    );
    points.push_back(p);
  }

全体

void triangulation(
  const vector &keypoint_1,
  const vector &keypoint_2,
  const std::vector &matches,
  const Mat &R, const Mat &t,
  vector &points) {
  Mat T1 = (Mat_(3, 4) <<
    1, 0, 0, 0,
    0, 1, 0, 0,
    0, 0, 1, 0);
  Mat T2 = (Mat_(3, 4) <<
    R.at(0, 0), R.at(0, 1), R.at(0, 2), t.at(0, 0),
    R.at(1, 0), R.at(1, 1), R.at(1, 2), t.at(1, 0),
    R.at(2, 0), R.at(2, 1), R.at(2, 2), t.at(2, 0)
  );

  Mat K = (Mat_(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);
  vector pts_1, pts_2;
  for (DMatch m:matches) {
    // 将像素坐标转换至相机坐标
    pts_1.push_back(pixel2cam(keypoint_1[m.queryIdx].pt, K));
    pts_2.push_back(pixel2cam(keypoint_2[m.trainIdx].pt, K));
  }

  Mat pts_4d;
  cv::triangulatePoints(T1, T2, pts_1, pts_2, pts_4d);

  // 转换成非齐次坐标
  for (int i = 0; i < pts_4d.cols; i++) {
    Mat x = pts_4d.col(i);
    x /= x.at(3, 0); // 归一化
    Point3d p(
      x.at(0, 0),
      x.at(1, 0),
      x.at(2, 0)
    );
    points.push_back(p);
  }
}

Point2f pixel2cam(const Point2d &p, const Mat &K) {
  return Point2f
    (
      (p.x - K.at(0, 2)) / K.at(0, 0),
      (p.y - K.at(1, 2)) / K.at(1, 1)
    );
}

3D-2D的PnP问题

线性解法

1. 把（R|t）写成3x4的矩阵

2. 则变成求解以下方程组：

 P3P：利用三角关系

 

 其中  三个cos已知，u，w也可以由A,B,C的世界坐标算出，x，y未知

BA法(最小重影误差)求PnP

理论

1. 优化位姿：求出关于误差的梯度  J

 优化空间位置：关于P的梯度 J

 2. 用高斯牛顿法求解

代码

1. 计算H和b

for (int iter = 0; iter < iterations; iter++) {
    Eigen::Matrix H = Eigen::Matrix::Zero();
    Vector6d b = Vector6d::Zero();

    cost = 0;
    // compute cost
    for (int i = 0; i < points_3d.size(); i++) {
      Eigen::Vector3d pc = pose * points_3d[i];
      double inv_z = 1.0 / pc[2];
      double inv_z2 = inv_z * inv_z;
      Eigen::Vector2d proj(fx * pc[0] / pc[2] + cx, fy * pc[1] / pc[2] + cy);

      Eigen::Vector2d e = points_2d[i] - proj;

      cost += e.squaredNorm();
      Eigen::Matrix J;
      J << -fx * inv_z,
        0,
        fx * pc[0] * inv_z2,
        fx * pc[0] * pc[1] * inv_z2,
        -fx - fx * pc[0] * pc[0] * inv_z2,
        fx * pc[1] * inv_z,
        0,
        -fy * inv_z,
        fy * pc[1] * inv_z2,
        fy + fy * pc[1] * pc[1] * inv_z2,
        -fy * pc[0] * pc[1] * inv_z2,
        -fy * pc[0] * inv_z;

      H += J.transpose() * J;
      b += -J.transpose() * e;
    }

 2. 求dx

    Vector6d dx;
    dx = H.ldlt().solve(b);

3. 优化

    pose = Sophus::SE3d::exp(dx) * pose;
    lastCost = cost;

3D-3D的ICP

SVD方法

问题：

 

 令

则对W进行SVD分解

得：R=U V^T

 3. t=p-Rp'

代码

void pose_estimation_3d3d(const vector &pts1,
                          const vector &pts2,
                          Mat &R, Mat &t) {
  Point3f p1, p2;     // center of mass
  int N = pts1.size();
  for (int i = 0; i < N; i++) {
    p1 += pts1[i];
    p2 += pts2[i];
  }
  p1 = Point3f(Vec3f(p1) / N);
  p2 = Point3f(Vec3f(p2) / N);
  vector q1(N), q2(N); // remove the center
  for (int i = 0; i < N; i++) {
    q1[i] = pts1[i] - p1;
    q2[i] = pts2[i] - p2;
  }

  // compute q1*q2^T
  Eigen::Matrix3d W = Eigen::Matrix3d::Zero();
  for (int i = 0; i < N; i++) {
    W += Eigen::Vector3d(q1[i].x, q1[i].y, q1[i].z) * Eigen::Vector3d(q2[i].x, q2[i].y, q2[i].z).transpose();
  }
  cout << "W=" << W << endl;

  // SVD on W
  Eigen::JacobiSVD svd(W, Eigen::ComputeFullU | Eigen::ComputeFullV);
  Eigen::Matrix3d U = svd.matrixU();
  Eigen::Matrix3d V = svd.matrixV();

  cout << "U=" << U << endl;
  cout << "V=" << V << endl;

  Eigen::Matrix3d R_ = U * (V.transpose());
  if (R_.determinant() < 0) {
    R_ = -R_;
  }

非线性优化方法

 

​​​​​​​