L1和L2正则化的三种不同角度的理解
观看B站视频后写的笔记,链接
降低模型复杂度>=正则化>=减小模型参数个数
0. 前言
正则化是一个专有名词,和正则表达式中的正则没有任何关系。L1和L2正则化就是用L1范数和L2范数来规范模型参数的这么一种方法,Dropout也叫正则化,但这两种方法天差地别。在花书中正则化的定义为凡是可以减少泛化误差而不是减少训练误差的方法都可以称作是正则化方法,即凡是能减少过拟合的方法都能被称作是正则化方法。
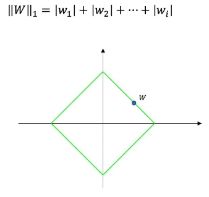
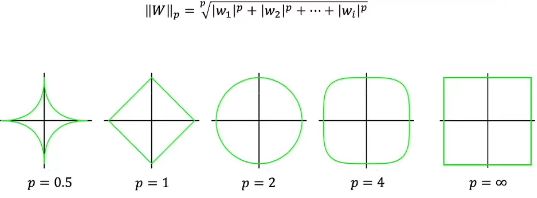
范数把空间中两点的距离这个概念进行了扩充。权重w可以理解为是一个高维的向量,也可以理解为在高维空间中的一个点,这个点到原点的距离如果是欧氏距离的话,那就是L2范数,如果把L2范数相同的点画出来就是一个圆,半径就为L2范数。L1范数也是类似。正则化一般只用到L1和L2范数,但范数按照定义有很多种类,如Lp范数,p可以取0到1之间的一个数(得到的集合为非凸集),也可以取大于等于1的一个数(此时构成的集合是一个凸集)。可行域是凸集的话就是一个凸优化问题。
1. 从拉格朗日乘数法的角度进行理解
在神经网络里,针对参数的正则化,就是针对权重w(w决定了模型曲线形状,b只会改变模型的平移偏置)的正则化。在神经网络的训练中,当收敛到损失函数的最小值时,w和b绝对值的大小不一定,所以会出现 当用训练集训练出一组较大的w和b后,图像中误差和噪声也被放大 的问题。所以就需要对权重w约束一个可行域范围,在这个范围内求最值,即拉格朗日乘数法的角度。
如下图所示,红色的线是损失函数的等高线,绿色的线是可行域范围,坐标轴分别表示w1和w2(更高维的w表示有更多的轴),在我们能找到在约束条件下的最值点。其中式子里的 λ C \lambda C λC 项对求最值点时的w不影响,因为求梯度时此项为0,但是此项决定了可行域范围即绿色线范围的大小。
拉格朗日函数中的拉格朗日乘子 λ \lambda λ作用是调节约束条件的梯度的大小,让他的大小和损失函数梯度J的大小相同方向相反。每一个不同交点的最值就能确定不同的 λ \lambda λ,反过来也是一样。另一方面也可以说其实只是引入了一个超参数C,只要确定了C,就可以计算出对应的 λ \lambda λ。当没有C时,就把 λ \lambda λ作为超参数进行调节。

L2正则化的极值点一般都在相切的圆上面,L1正则化的极值点一般都在坐标轴上(此时某些权重w为0,可以带来稀疏性和选择特征性,即某些特征起作用 或 特征之间去耦合 或 解决过拟合)

问题(存疑):正则化对权重进行了一个约束,在约束范围内即绿线范围内,会不会导致求出极值点时的偏差过大?
作者认为不会。因为min J(W, b)= min J(k·W, k·b),所以权重存在一个线性解空间,在下述二维空间的图中用红色的虚线来表示,那么此时偏差就可以表示成极值点和线性解空间之间的距离即垂直距离。所以并不是说可行域范围的框框越小偏差越大。
2. 从权重衰减的角度进行理解
上面拉格朗日乘数法就是去控制权重到原点之间的距离,通过这样的方式去约束权重的取值。
损失函数: J ( W , b ) J(W,b) J(W,b)
权重更新: W = W − η ⋅ ∇ W J ( W ) W=W-\eta·{\nabla_W} J(W) W=W−η⋅∇WJ(W)
正则化后的损失函数: J ^ ( W ) = J ( W ) + λ ∣ ∣ W ∣ ∣ 2 = J ( W ) + α 2 W T W \hat{J}(W)=J(W)+\lambda||W||_2=J(W)+\frac{\alpha}{2}W^TW J^(W)=J(W)+λ∣∣W∣∣2=J(W)+2αWTW
正则化后的权重更新: W = W − η ⋅ ∇ W J ^ ( W ) = ( 1 − η ⋅ α ) W − η ⋅ ∇ W J ( W ) W=W-\eta·{\nabla_W} \hat{J}(W)=(1-\eta·\alpha)W-\eta·{\nabla_W} J(W) W=W−η⋅∇WJ^(W)=(1−η⋅α)W−η⋅∇WJ(W)
从公式中可以看出,权重w前面的系数 η \eta η和 α \alpha α两个超参数相乘小于1大于0的时候,每一次权重更新后权重都要进行一些缩小。所以权重衰减就衰减在W前面的系数上,相当于增加了一个惩罚项,每一次学习都惩罚一点让权重取值不至于太大。如果对模型要拟合的数据曲线进行泰勒展开后,W变小会使高次项的某个系数 f ( n ) ( a 0 ) → 0 f^{(n)}(a_0)→0 f(n)(a0)→0。并且只惩罚大于1次的高次项,因为0次项和一次项的自变量权重系数减小并不会对拟合曲线的形状产生变化。

L2正则化和L1正则化
如果用 J ( W ∗ ) J(W^*) J(W∗)表示损失函数, J ^ ( W ^ ) \hat{J}(\hat{W}) J^(W^)表示正则化后的损失函数,其中 W ∗ W^* W∗和 W ^ \hat{W} W^表示到达极值点时对应的权重(是一个线性解空间)。要想得到正则化后的极值点对应权重 W ^ \hat{W} W^ 相对于 原来 W ∗ W^* W∗的缩减倍数,就要得到 W ∗ W^* W∗和 W ^ \hat{W} W^之间的关系表达式。以下是推导过程:
对于普通的损失函数来说,根据在 W ∗ W^* W∗处的二阶泰勒展开,近似有,(其中H为海塞矩阵,和 W ∗ W^* W∗一起为常量, ∇ W J ( W ∗ ) = ∇ W J ^ ( W ^ ) = 0 \nabla_WJ(W^*)=\nabla_W\hat{J}(\hat{W})=0 ∇WJ(W∗)=∇WJ^(W^)=0)
J ( W ) ≈ J ( W ∗ ) + ∇ W J ( W ∗ ) ( W − W ∗ ) + 1 2 ( W − W ∗ ) T H ( W − W ∗ ) = J ( W ∗ ) + 1 2 ( W − W ∗ ) T H ( W − W ∗ ) ⇒ ∇ W J ( W ) = H ( W − W ∗ ) J(W)≈J(W^*)+\nabla_WJ(W^*)(W-W^*)+\frac{1}{2}(W-W^*)^TH(W-W^*)=J(W^*)+\frac{1}{2}(W-W^*)^TH(W-W^*) \Rightarrow \nabla_WJ(W)=H(W-W^*) J(W)≈J(W∗)+∇WJ(W∗)(W−W∗)+21(W−W∗)TH(W−W∗)=J(W∗)+21(W−W∗)TH(W−W∗)⇒∇WJ(W)=H(W−W∗)
- 如果对自变量为W的损失函数进行
L2正则化,
J ^ ( W ) = J ( W ∗ ) + 1 2 ( W − W ∗ ) T H ( W − W ∗ ) + α 2 W T W ⇒ ∇ W J ^ ( W ) = H ( W − W ∗ ) + α ⋅ W \hat{J}(W)=J(W^*)+\frac{1}{2}(W-W^*)^TH(W-W^*)+\frac{\alpha}{2}W^TW \Rightarrow \nabla_W\hat{J}(W)=H(W-W^*)+\alpha·W J^(W)=J(W∗)+21(W−W∗)TH(W−W∗)+2αWTW⇒∇WJ^(W)=H(W−W∗)+α⋅W
有了上述式子后,就可以求梯度,在 W ^ \hat{W} W^处 J ^ ( W ) \hat{J}(W) J^(W)的梯度为0。从而得到 W ∗ W^* W∗和 W ^ \hat{W} W^之间的关系。可以明显看到, W i ^ = λ i λ i + α ⋅ W i ∗ \hat{W_i}=\frac{\lambda_i}{\lambda_i+\alpha}·W^*_i Wi^=λi+αλi⋅Wi∗,如果 α = 0 \alpha=0 α=0,两者相等;如果 α > 0 \alpha>0 α>0, W ^ \hat{W} W^就相当于要对 W ∗ W^* W∗进行缩小;如果 α < 0 \alpha<0 α<0, W ^ \hat{W} W^就相当于要对 W ∗ W^* W∗进行放大。也就是说L2正则化,本质上就是对原来的 W ∗ W^* W∗进行缩放。

2. 如果对自变量为W的损失函数进行L1正则化(前提条件为海塞矩阵是对角阵,这样可以简化问题),
J ^ ( W ) = J ( W ∗ ) + 1 2 ( W − W ∗ ) T H ( W − W ∗ ) + α ∣ ∣ W ∣ ∣ 1 = J ( W ∗ ) + ∑ i n ( 1 2 H i , i ( W i − W i ∗ ) 2 + α ∣ W i ∣ ) ⇒ ∇ W J ^ ( W ) = H ( W − W ∗ ) + α ⋅ s i g n ( W ) \hat{J}(W)=J(W^*)+\frac{1}{2}(W-W^*)^TH(W-W^*)+\alpha||W||_1=J(W^*)+\sum_{i}^{n}(\frac{1}{2}H_{i,i}(W_i-W^*_i)^2+\alpha|W_i|) \Rightarrow \nabla_W\hat{J}(W)=H(W-W^*)+\alpha·sign(W) J^(W)=J(W∗)+21(W−W∗)TH(W−W∗)+α∣∣W∣∣1=J(W∗)+∑in(21Hi,i(Wi−Wi∗)2+α∣Wi∣)⇒∇WJ^(W)=H(W−W∗)+α⋅sign(W)
同样可以得到 W ∗ W^* W∗和 W ^ \hat{W} W^之间的关系式 W i ^ = W i ∗ − α ⋅ s i g n ( W i ) ^ H i , i \hat{W_i}=W_i^*-\frac{\alpha·sign(\hat{W_i)}} {H_{i,i}} Wi^=Wi∗−Hi,iα⋅sign(Wi)^。此时分类讨论的时候比之前L2正则化时要麻烦的多,讨论结果如下图所示。从中可以看出,当 W ∗ W^* W∗在两端都是闭区间的区间内时,正则化后的权重会变成0,正是L1正则化带来稀疏性的情况!


3. 从贝叶斯的角度进行理解
损失函数 本质上和 概率分布是等价的。这一块在我之前的RLE损失函数相关的博客中有相关的详细介绍。RLE
似然是似然函数(是一个概率分布函数),最大似然值是这个函数的最大值(是一个确定的概率值)。