python 一元回归拟合(含幂函数,对数,S函数,指数函数,一次、二次、三次,逆函数,生长、复合函数)
提示
目录
因为工作最近需要对数据进行拟合生成指标
一、最后的成果
二、导入数据
三、将数据中的自变量因变量都抽出来,进行九种回归拟合
1.代码如下:
2.这里补充下变换知识
三 对数据进行绘图,画出拟合曲线和散点图,把公式也写上去
总结:撒花~写完了这里
因为工作最近需要对数据进行拟合生成指标
所以打算写一个含有十种函数的拟合模型,去看那种拟合的r2最高,将r2最高的函数函数作为最终拟合函数。
一、最后的成果
用n 组数据生产 n组数据 拟合十种回归,保留r2最大的画出期曲线和散点图,标注好函数公式,(图是假数据,已经打码处理,大概理解下就行)
下是本篇文章正文内容,下面案例可供参考
二、导入数据
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
##
io=r'C:\Users\Viki\Desktop\****'#根据自己的需要换
city_pr2=pd.read_excel(io,sheet_name='Sheet1')三、将数据中的自变量因变量都抽出来,进行九种回归拟合
1.代码如下:
df_d = pd.DataFrame(columns=('名称','类型','r2','系数'))
from sklearn.metrics import r2_score
#我这里原本是写了循环的 因为这种回归,肯定不是一组数据进行十种回归,这样还不如用spss
#所以这里是有 city_pr2['标签']==i 里面每个标签拿出来的数据都回归十次,选出每组数据r2最大的回归#函数,感觉大家都会加循环,我就不删了,方便大家改,可能让人难懂~算了随缘
for i in a:
jj=city_pr2[(city_pr2['位置']==i)]
# jj=city_pr2
#十种函数的回归从这里开始写了~
##线性
x_data_2=jj[['自变量']].values.tolist()
y_data_2=jj[['因变量']].values.tolist()
x_data_2=sum(x_data_2,[])
y_data_2=sum(y_data_2,[])
L=np.polyfit(x_data_2, y_data_2, 1)
print(L)
Z=np.polyval(L,x_data_2,)
score = r2_score(y_data_2, Z, multioutput='raw_values')
print('线性:'+str(score))
new=pd.DataFrame({'名称':i,
'类型':'线性',
'r2':score,
'系数':[L]})
df_d=df_d.append(new,ignore_index=(True))
##指数
x_data_2=jj[['自变量']].values.tolist()
y_data_2=jj[['因变量']].values.tolist()
x_data_2=sum(x_data_2,[])
y_data_2=sum(y_data_2,[])
L=np.polyfit(x_data_2, np.log(y_data_2), 1)
Z=np.polyval(L,x_data_2)
true=np.exp(Z)
score = r2_score(y_data_2,true, multioutput='raw_values')
print('指数:'+str(score))
new=pd.DataFrame({'名称':i,
'类型':'指数',
'r2':score,
'系数':[L]})
df_d=df_d.append(new,ignore_index=(True))
##二次
x_data_2=jj[['自变量']].values.tolist()
y_data_2=jj[['因变量']].values.tolist()
x_data_2=sum(x_data_2,[])
y_data_2=sum(y_data_2,[])
L=np.polyfit(x_data_2, y_data_2, 2)
print(L)
Z=np.polyval(L,x_data_2,)
score = r2_score(y_data_2, Z, multioutput='raw_values')
print('二次:'+str(score))
new=pd.DataFrame({'名称':i,
'类型':'二次',
'r2':score,
'系数':[L]})
df_d=df_d.append(new,ignore_index=(True))
##幂函数
x_data_2=jj[['自变量']].values.tolist()
y_data_2=jj[['因变量']].values.tolist()
x_data_2=sum(x_data_2,[])
y_data_2=sum(y_data_2,[])
L=np.polyfit(np.log(x_data_2), np.log(y_data_2), 1)
Z=np.polyval(L,np.log(x_data_2))
true=np.exp(Z)
score = r2_score(y_data_2,true, multioutput='raw_values')
print('幂函数:'+str(score))
new=pd.DataFrame({'名称':i,
'类型':'幂函数',
'r2':score,
'系数':[L]})
df_d=df_d.append(new,ignore_index=(True))
##对数
x_data_2=jj[['自变量']].values.tolist()
y_data_2=jj[['因变量']].values.tolist()
x_data_2=sum(x_data_2,[])
y_data_2=sum(y_data_2,[])
L=np.polyfit(np.log(x_data_2), y_data_2, 1)
Z=np.polyval(L,np.log(x_data_2))
score = r2_score(y_data_2,Z, multioutput='raw_values')
print('对数:'+str(score))
new=pd.DataFrame({'名称':i,
'类型':'对数',
'r2':score,
'系数':[L]})
df_d=df_d.append(new,ignore_index=(True))
##复合函数
x_data_2=jj[['自变量']].values.tolist()
y_data_2=jj[['因变量']].values.tolist()
x_data_2=sum(x_data_2,[])
y_data_2=sum(y_data_2,[])
L=np.polyfit(x_data_2,np.log(y_data_2), 1)
Z=np.polyval(L,x_data_2)
true=np.exp(Z)
score = r2_score(y_data_2,true, multioutput='raw_values')
print('复合函数:'+str(score))
new=pd.DataFrame({'名称':i,
'类型':'复合函数',
'r2':score,
'系数':[L]})
df_d=df_d.append(new,ignore_index=(True))
##生长
x_data_2=jj[['自变量']].values.tolist()
y_data_2=jj[['因变量']].values.tolist()
x_data_2=sum(x_data_2,[])
y_data_2=sum(y_data_2,[])
L=np.polyfit(x_data_2, np.log(y_data_2), 1)
Z=np.polyval(L,x_data_2)
true=np.exp(Z)
score = r2_score(y_data_2,true, multioutput='raw_values')
print('生长:'+str(score))
new=pd.DataFrame({'名称':i,
'类型':'生长',
'r2':score,
'系数':[L]})
df_d=df_d.append(new,ignore_index=(True))
##三次
x_data_2=jj[['自变量']].values.tolist()
y_data_2=jj[['因变量']].values.tolist()
x_data_2=sum(x_data_2,[])
y_data_2=sum(y_data_2,[])
L=np.polyfit(x_data_2, y_data_2, 3)
Z=np.polyval(L,x_data_2)
score = r2_score(y_data_2,Z,multioutput='raw_values')
print('三次:'+str(score))
new=pd.DataFrame({'名称':i,
'类型':'三次',
'r2':score,
'系数':[L]})
df_d=df_d.append(new,ignore_index=(True))
##S函数
x_data_2=jj[['自变量']].values.tolist()
y_data_2=jj[['因变量']].values.tolist()
x_data_2=sum(x_data_2,[])
x_cz_3 = [1/x for x in x_data_2]
y_data_2=sum(y_data_2,[])
L=np.polyfit(x_cz_3, np.log(y_data_2), 1)
Z=np.polyval(L,x_cz_3)
true=np.exp(Z)
score = r2_score(y_data_2,true,multioutput='raw_values')
print('S函数:'+str(score))
new=pd.DataFrame({'名称':i,
'类型':'S函数',
'r2':score,
'系数':[L]})
df_d=df_d.append(new,ignore_index=(True))
##逆函数
x_data_2=jj[['自变量']].values.tolist()
y_data_2=jj[['因变量']].values.tolist()
x_data_2=sum(x_data_2,[])
x_cz_3 = [1/x for x in x_data_2]
y_data_2=sum(y_data_2,[])
L=np.polyfit(x_cz_3, y_data_2, 1)
Z=np.polyval(L,x_cz_3)
score = r2_score(y_data_2,true,multioutput='raw_values')
print('逆函数:'+str(score))
new=pd.DataFrame({'名称':i,
'类型':'逆函数',
'r2':score,
'系数':[L]})
df_d=df_d.append(new,ignore_index=(True))
#把没组函数的r2最大的拿出来
df_data=df_d.sort_values('r2', ascending=False).groupby('名称', as_index=False).first()
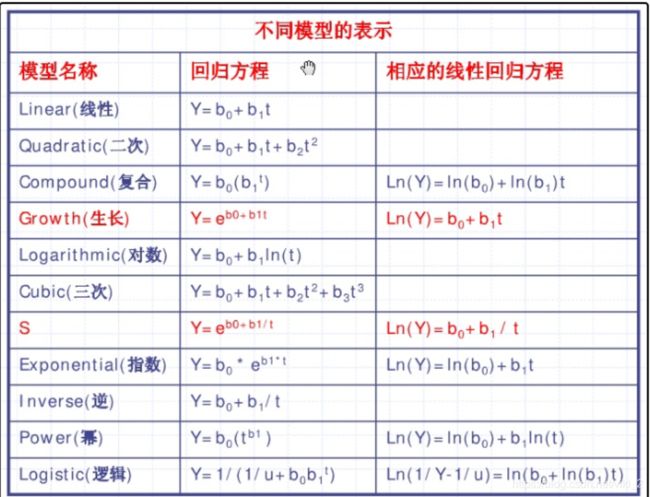
2.这里补充下变换知识
回归用的都是最小二乘法,将8种函数进行变换(不包括二次、三次),变换成线性。变换方式如下,python也是根据这个变换去写的。
三 对数据进行绘图,画出拟合曲线和散点图,把公式也写上去
ff=df_data
# second=df_e[(df_e['类型']=='二次')]
j=0
while j< 59: #这里是我不够聪明,我自己数了一下我总共有多少组数据,所以加了个while 限制绘图次数
gg=ff.iloc[[j]].values.tolist()
gg =sum(gg,[])
#开始写公式 自变量 &因变量
if gg[1] == '二次':
x=np.arange(0.15,0.4,0.002)
y_data=gg[3][0]*x**2+gg[3][1]*x+gg[3][2]
formu_s='y_data='+str(gg[3][0])+str('x^2+')+str(gg[3][1])+str('x')+str('+(')+str(gg[3][2])+str(')')
elif gg[1] == '线性':
x=np.arange(0.15,0.4,0.002)
y_data=gg[3][0]*x+gg[3][1]
formu_s='y_data='+str(gg[3][0])+str('x')+str('+(')+str(gg[3][1])+str(')')
elif gg[1] == '指数':
x=np.arange(0.15,0.4,0.002)
y_data=np.exp(gg[3][0]*x+gg[3][1])
formu_s='y_data='+str(np.exp(gg[3][1]))+str('e')+'^'+str(gg[3][0]) +'x'
elif gg[1] == '幂函数':
x=np.arange(0.15,0.4,0.002)
y_data=np.exp(gg[3][1]+(np.log(x)*gg[3][0]))
formu_s='y_data='+str(np.exp(gg[3][1]))+str('x')+'^'+str(gg[3][0])
elif gg[1] == '对数':
x=np.arange(0.15,0.4,0.002)
y_data=gg[3][1]+(np.log(x)*gg[3][0])
formu_s='y_data='+str(gg[3][1])+'+'+str(gg[3][0])+'In(x)'
elif gg[1] == '生长':
x=np.arange(0.15,0.4,0.002)
y_data=np.exp(gg[3][0]*x+gg[3][1])
formu_s='y_data='+'e^('+str(gg[3][0])+str('x')+str('+(')+str(gg[3][1])+str('))')
elif gg[1] == '三次':
x=np.arange(0.15,0.4,0.002)
y_data=gg[3][0]*x**3+gg[3][1]*x**2+gg[3][2]*x+gg[3][3]
formu_s='y_data='+str(gg[3][0])+str('x^3+')+str(gg[3][1])+str('x^2+')+str(gg[3][2])+str('x')+str('+(')+str(gg[3][3])+str(')')
elif gg[1] == 'S函数':
x=np.arange(0.15,0.4,0.002)
y_data=np.exp(gg[3][0]*(x)**(-1)+gg[3][1])
formu_s='y_data='+'e^('+str(gg[3][0])+str('(1/x)')+str('+(')+str(gg[3][1])+str('))')
elif gg[1] == '逆函数':
x=np.arange(0.15,0.4,0.002)
y_data=gg[3][0]*(x)**(-1)+gg[3][1]
formu_s='y_data='+str(gg[3][0])+str('(1/x)')+str('+(')+str(gg[3][1])+str(')')
elif gg[1] == '复合函数':
x=np.arange(0.15,0.4,0.002)
y_data=np.exp(gg[3][1]+(gg[3][0]*x))
formu_s='y_data='+str(np.exp(gg[3][1])) +'*'+str(np.exp(gg[3][0])) +'^x'
gg.append(formu_s)
del gg[3]
gg=[gg]
df_a=df_a.append(gg,ignore_index=(True))
plt.plot(x,y_data,'r-.o',label='因变量 '+formu_s+' r2='+str(gg[0][2]),linewidth=0.02)
plt.xlabel('自变量',fontsize=20)
plt.ylabel('因变量',fontsize=20)
plt.title(str(gg[0][0])+'自变量&因变量',fontsize=20) #要用plt调动title
plt.legend(fontsize=20)
x2=city_pr2[(city_pr2['位置']==gg[0][0])][['自变量']]
y2=city_pr2[(city_pr2['位置']==gg[0][0])][['因变量']]
colors1 = '#00CED1' #点的颜色
colors2 = '#DC143C'
area = np.pi * 6**2 # 点面积
# 画散点图
plt.scatter(x2, y2, s=area, c=colors2, alpha=0.5, label='ZH')
plt.savefig('')
io_1=r'C:\Users\Viki\Desktop\临时文件'
plt.savefig(io_1+'/%s_zh.jpg'%(gg[0][0]), bbox_inches='tight')
plt.show()
plt.close()
j=j+1
if j > 58:
break