基于K均值聚类算法的图像分割（Matlab）

一、K均值聚类算法是什么？

1、什么是聚类？

聚类是指通过既定的规则把物理或者抽象的集分成几个由类似特征的样本组成的类的过程。复杂点说，聚类指用一种类似性度为标准，将类似的样本划分到同一个组中，最终得到多个类。下图为聚类的过程。

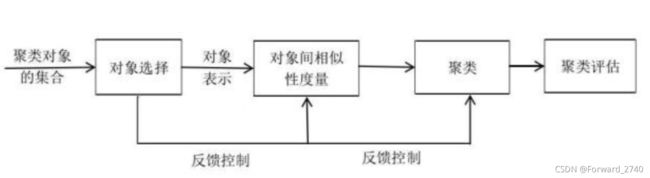
图1-聚类的过程

2、初探K均值聚类算法

K- means算法是一种迭代运算的算法。K-means因其简便、有效的特点，使得其被使用的频率非常之高。除此之外，K-means聚类算法还非常易于理解。只要给定数据和聚类数K值，K-means聚类算法就会根据距离算法将数据分成K个群。K-Means中使用的算法方法非常简单，可以使用下面的一系列图直观地说明。

图2-K均值聚类示意图
上面图a为初始数据集合，我们假设k = 2。图b中,我们随机选择k类对应红蓝两个类别，即图中红色叉叉和蓝色叉叉，之后计算所有数据到两个叉叉的距离，记录每个数据离的最近的叉叉数据的类别。上面图C，我们得到了第一次迭代后所有数据点的类别。在这之后，我们更新现在的红点和蓝点的新质心，新的质心位置发生了改变。如图所示，图e和图f重复图c和图d的过程。也就是说，将所有的数据点类别标记为最近的质心所属的类别，找到新的质心。最后，我们得到了两个类，如图f所示。

3、K均值算法的原理与理解

Kmeans算法是最常用的聚类算法。主要的想法是给出每个点(指数据记录)初始集群的k个中心点的值和聚类数量K值，把每个点分配到离的最近的聚类中心点所代表的群中，之后重新计算集群的中心点,一个群中所有点取均值即为新的中心点,然后把点的求解和更新了集群的中心,之后一直迭代，直到点中心点调整很小或者达到特定迭代次数很少。
假设特定的X数据样本包含n个对象X = {x1，x2， x3，…，xn}，X中每个对象都有m维的属性。Kmeans算法将根据对象之间的相似性、相同处，将n个对象聚合为k个指定的集群。每个对象属于集群，属于离集群中心距离最小的集群。在Kmeans的情况下，有k个集群中心(c1，c2，c3…ck}， 1 < k≤n，在这之后，计算各个点到各个集群中心的欧几里得距离，如公式：

上面的式子里，表示第j个聚类中心的1 ≤ j ≤ k，表示第i个样本1 ≤ i ≤ n，表示第i个对象的第t个属性，1 ≤ t ≤ m，表示第j个聚类中心的第t个属性。之后依次比较每个样本到每一个聚类中心的距离，把样本安排到距离最近的聚类中心的类簇中，得到k个类簇{ S 1 , S 2 , S 3 , . . . , S k }
Kmeans算法是以中心定义类簇的原型，它的类簇中心就是类簇内所有样本在每个维度的均值，它的计算公式如下：

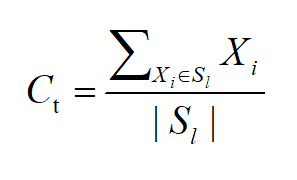
上面的式子里，Xl表示第l个类簇中第i个样本，Cl表示第l个聚类的中心，1 ≤ l ≤ k，∣Sl∣表示第l个类簇中样本的个数，1 ≤ i ≤ ∣Sl∣。

二、K均值聚类算法如何在图像分割上应用？

图像分割技术利用图像的基本特点把图像分割成为多个不同的集合，在一个集合里面的数据具有类似性，在不同集合里的数据有可以区别划分的地方。对图像进行聚类时，首先也是最重要的，要将图像的特点提取为数据。研究人员经常选择灰度图像、彩色图像等等使用算法做聚类分析，用来验证聚类算法的是否实现。
一般图像都是基于红、蓝、绿三种颜色（三种通道）构成的，不过弧度图像的通道像素值时用灰度变化来表示的。即蓝、红、绿这几个通道是用不一样的灰度色阶表示的。灰度色阶代表从浅到深不同颜色的变化，这样的灰度色阶一共有256种。在灰度图像中，图像的不同的根本是因为灰度的不同与变化。聚类分割灰度图像，就是把灰度差别大的分割出来，把灰度差别小的分为同一族。
k-means算法通常用于特定的理论图像分割方法。就单色图像来说，亮度是图像被分割的信息，不过彩色图像不同，其不只有亮度，还包含饱和度。当分割彩色图像时，必须挑选一个适合的彩色空间。目前使用的彩色空间有三个，RGB、GMY和YUV。在RGB彩色空间中，可以使用R(红)、G(绿)、B(蓝)这三个组件来表示任何颜色的光。GMY的彩色空间和RGB空间的不同之处在于，它的颜色是通过从白光减去一些成分得出的。RGB比色空间的颜色是通过在黑光中加入一定的颜色而得到的。而YUV空间里，两色度符号U、V与亮度Y是对应的。彩色图像的每个像素都对应三维空间里的一个点，三维空间对应于红、蓝、绿这三种颜色的强度。基于聚类算法Kmeans的图像分割使用图像像素作为数据点，根据定好的聚类数量进行聚类，最后用相应的聚类中心替换每个像素进行图像重建。从图中可以看出，当集群值K不同时，不同的颜色特征。

图3-不同聚类值K时图像分割效果

三、Matlab仿真

K均值聚类算法程序

function [C, label, J] = kmeans(I, k) 
[m, n, p] = size(I);%图片的大小m*n，p代表RGB三层
X = reshape(double(I), m*n, p);
rng('default');
C = X(randperm(m*n, k), :);%随机选三个聚类中心
J_prev = inf; iter = 0; J = []; tol = 1e-11;%容忍度tol，inf为无穷大
 
while true,
    iter = iter + 1;
    dist = sum(X.^2, 2)*ones(1, k) + (sum(C.^2, 2)*ones(1, m*n))' - 2*X*C';%计算图片中各个点到K个聚类中心的距离
    [~,label] = min(dist, [], 2) ;  %label记录最小值的行数
    for i = 1:k,
       C(i, :) = mean(X(label == i , :)); %取新的k个聚类中心
    end
    J_cur = sum(sum((X - C(label, :)).^2, 2));%距离之和
    J = [J, J_cur];
    display(sprintf('#iteration: %03d, objective fcn: %f', iter, J_cur));
    if norm(J_cur-J_prev, 'fro') < tol,% A和A‘的积的对角线和的平方根，即sqrt(sum(diag(A'*A)))，本次与上次距离之差
        break;
    end
    if (iter==10),% A和A‘的积的对角线和的平方根，即sqrt(sum(diag(A'*A)))，本次与上次距离之差
        break;
    end
    J_prev = J_cur;
end

主程序

clear all; close all;
I = imread('C:\Users\Administrator\Desktop\K_medoids分类\de.jpg');%读取图片数据编程矩阵
[m, n, p] = size(I);
 
%figure();
%I=imnoise(I1,'salt & pepper',0.1);%椒盐噪声，通常是由图像传感器，传输信道，解压处理等产生的黑白相间的亮暗点噪声（椒-黑，盐-白）。通常出现在灰度图中。
I1 = imnoise(I,'gaussian',0,0.1) ;% 高斯噪声，顾名思义是指服从高斯分布（正态分布）的一类噪声，通常是因为不良照明和高温引起的传感器噪声。通常在RGB图像中，显现比较明显。
%imshow(I);%显示图片I
%title('加噪图像');
 
k = 2;
[C, label, J2] = kmeans1(I, k);
I_seg2 = reshape(C(label, :), m, n, p);%转换成图片矩阵的格式
k = 3;
[C, label1, J3] = kmeans2(I, k);
I_seg3 = reshape(C(label1, :), m, n, p);
k = 4;
[C, label, J2] = kmeans1(I1, k);
I_seg4 = reshape(C(label, :), m, n, p);
k = 8;
[C, label1, J3] = kmeans2(I1, k);
I_seg5 = reshape(C(label1, :), m, n, p);
 
figure
subplot(2, 3, 1), imshow(I, []), title('原图')
subplot(2, 3, 2), imshow(uint8(I_seg2), []), title('2聚类')
subplot(2, 3, 3), imshow(uint8(I_seg3), []), title('3聚类')
subplot(2, 3, 4), imshow(uint8(I_seg4), []), title('4聚类')
subplot(2, 3, 5), imshow(uint8(I_seg5), []), title('8聚类')
 
figure
subplot(3, 3, 1),plot(1:length(J2), J2), xlabel('#iterations')
subplot(3, 3, 2),plot(1:length(J3), J3), xlabel('#iterations')
subplot(3, 3, 3),plot(1:length(J4), J4), xlabel('#iterations')
subplot(3, 3, 4),plot(1:length(J5), J5), xlabel('#iterations')
 
segmented_images = cell(1,3);%1*3矩阵
rgb_label = repmat(label1,[1 1 3]);%把label矩阵编程[1 1 3]的矩阵
 
for k = 1:10
    color = I;
    color(rgb_label ~= k) = 0;%把label不等于K的点除去
    segmented_images{k} = color;
end
 
figure(),imshow(segmented_images{1}), title('分割结果——区域1');
figure(),imshow(segmented_images{2}), title('分割结果——区域2');
figure(),imshow(segmented_images{3}), title('分割结果——区域3');

设置聚类值为K=2,3,4,8,20,40,100,200,500,1000运行代码，查看最终的运行效果图能否满足实验预期。

图4-K均值聚类分割图像-聚类图1

图5-K均值聚类分割图像-聚类图2
如图，可以看到，K均值聚类算法，成功的将输入的原图分割成K部分。2聚类图中，图片被分割成两部分，分别显示褐色和蓝色。且可以明显的分辩出，分割出的两部分聚类的形状、色彩与原图的色彩和图中物体的形状存在密切关联。当聚类值K=20时，输出的图像与原图就已经很相似。观察10张聚类输出图和原图，我们发现，当设置的循环跳出条件Tol为定值时(即当连续两次迭代聚类中心的变化值小于忍耐值Tol时，跳出循环)，随着聚类值K越高，基于K均值聚类的图像分割的效果越好，还原的图片与原图更接近。实验结果达到预期图片分割效果。