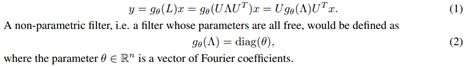Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering 论文阅读

Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering

Code link：https://github.com/mdeff/cnn_graph

 

目录

目录

1引言... 1

2 提出的方法... 1

2.1 学习快速定位谱过滤器... 2

2.2图的粗化... 3

3相关工作... 4

3.1 图信号处理... 4

3.2 在非欧式空间的cnn. 4

4 数字分析实验... 5

4.1 重访经典cnn在Mnist 数据集... 5

4.2 文本分类20news. 5

4.3 比较谱过滤器与计算效率... 6

4.4 图片质量的影响... 7

5 结论与未来的工作... 7

References. 8

 

 

摘要：我们的工作主要是在于从低纬规则化数据生成的CNN，（图片/视频/语音）转化到高纬度不规则区域，比如说社会社交网络/脑连接/词嵌入等通过图来表示；提出了一种基于谱图的CNN算法，为设计快速的卷积滤波器提供了必要的数学基础理论与数值分析；重要的是提出的算法与经典CNN具有相同的计算复杂度与恒定的学习复杂度，其通用于图结构，实验表明能够学习图的局部/统计/组成特征。

1引言

CNN【19】因其通过局部特征并汇聚其形成多尺度高纬信息在图像等领域取得突破，归因于卷积核抽取信息，可实现尺度的由大到小的转换；在用户数据网络/生物网络/远程日志信息网络/文档/词嵌入等领域的信息都是不规律非欧式域的，其都可以通过图来描述，存在异构的信息关系；对于图的几何框架的研究需要较强的数学理论比如说谱图理论【6】

卷积神经网络在图上的应用并不是直接的卷积与池化操作，无论是在理论与实践方面，定义图过滤器对评估与学习特征起到至关重要的作用 ，本文的贡献如下：

（1）、谱制定，基于图信号处理的谱图理论在图上CNN的应用【31】

（2）、定位过滤器，提出的谱过滤器是定位在以K为半径的球的【4】

（3）、低计算复杂度，计算复杂度是线性的；

（4）、高效的池化，提出的池化策略，将顶点重排为二叉树结构

（5）、实验结果，进行多组实验最终形成有用的模型，高效计算与精度与复杂度都优于之前的谱图CNN【4】，同样展示了谱图与经典CNN可达到同样的效果；

 

2 提出的方法

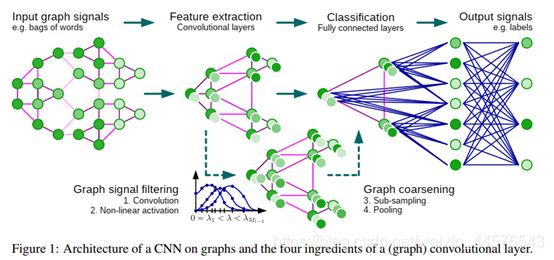
在图上的CNN需要三个步骤，（1）在图上的定位卷积滤波器的设计（2）相似顶点的放在一 起作粗化处理（3）对于空间高分辨率的图池化操作

2.1 学习快速定位谱过滤器

存在两种卷积策略，分别是空间与频谱的角度出发，通过对比，空间是提供卷积核，理论上行得通，但是面临匹配局部邻居节点的匹配挑战【4】，空间卷积并未有完整的数学定于；另一方面，【31】提供很好的卷积定位操作，卷积理论的定位作为线性在傅里叶上对角化的操作，然而图谱域的定位平移操作O（n）的乘法操作，可以通过对过滤器参数的选择来克服这些问题；

图傅里叶转化：

研究主要在无向连接图，g=(V , E ,W),v 顶点  E是边，W是节点之间的领矩阵，【6】图谱上的拉普拉斯的操作，其包含L=D-W D 是对角度矩阵，归一化拉普拉斯矩阵是L=In-D^-1/2WD-1/2  In是单位矩阵，L是实对称半正定矩阵，有正交向量对应非负奇异值；拉普拉斯是傅里叶基U=｛uo,u1…un-1｝,L =UAUT  A=diag{r0,r1…rn-1}, x=UT x ,x=Ux 在【31】中，如空间卷积一样，转化使得基本操作得以形成；

图信号的谱过滤器：

因为在顶点域不能表达有意义的转化操作，在图上的卷积攒机操作定义在傅里叶域x*g 

 

多项式参数应在定于卷积器：

无参数过滤器存在两个限制，不能在空间上定位，学习复杂度为O（n），使用多项式过滤器可以解决这个问题

 

参数Q是多项式系数向量，顶点j过滤器的值是顶点i，

，在【12 lemma 5.2】dg(I,j)>K  dg()是最短路径；例如两个顶点的最小表的数量，最后谱过滤器通过拉普拉斯的Kth 顺序的多项式，另外，学习复杂度为O（K），因此复杂度如同经典CNN

 

递归公式化快速过滤器：

展示k个参数的定位过滤器，因为傅里叶基的乘法器O（n），使用多项式可以运用，使得O（K|e|），使用多项式，使用信息化处理的核函数如小波函数【12】中，另外一个是the lanczos 算法【33】构建正交基，Kk(L ,x)=span{x,Lx,….Lk-1x} 独立的系数，然而其更复杂是未来的工作；

利用切比雪夫不等式，多项式形成正交基，希尔伯特空间的平方函数参考dyJ1-y2 

过滤器参数可以被截断k-1的顺序，切比雪夫参数是参数，可以写成

 

学习过滤器：

2.2图的粗化

池化操作需要有意义的领节点和相似的节点聚集，多尺度图保留几何特征，然后图上是NP-hard问题【5】，然而存在多种聚集算法，比如说谱聚类【21】，我们更注重的是每层的粗化相对于不同分辨率的数据域，并且聚类方法需要减少图的大小通过因子，在本文中利用graclus多层聚类算法粗化【9】，图代数多数方法【28】和kron 的减少【32】是两个值得探索的方法在未来的工作中；【9】，【16】使用贪心算法来计算连续的粗化缩小图谱聚类，其选择最小的减少【30】，匹配节点被探索，可以迅速的分成两类节点存在孤立点与非匹配点

2.3 图的快速池化

 

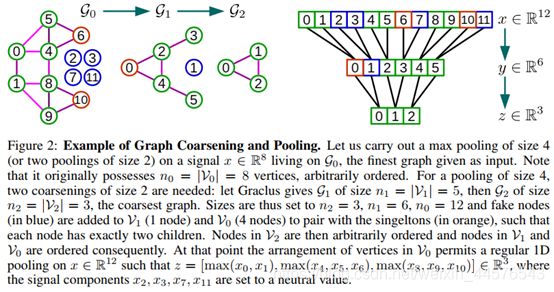
池化被反复执行多次很有效，在粗化后，输入的顶点其粗化的版本并不能进行有意义的方式排列，因此直接的使用池化不能保存所有匹配的节点，导致内存的低效率，并行计算很难实现，然而进行排列顶点可以变得高效，第一，建立平衡的二叉树第二重拍节点；粗化操作之后，每个节点有两个孩子节点，最后一层得到匹配，如果是孤立节点，有一个孩子节点，另一个是假节点；未连接的节点需要添加两个孤立节点作为还在节点，这种结构是平衡二叉树，规律的节点数量，孤立节点或者是孤立节点和一个假节点；假的节点需要跟随两个假节点；

假节点需要用中值来表示；因为假节点是人为的增加节点维度，所以说增加计算机代价，发现，实际上，通过Graclus算法遗留的孤立点很少，最粗的位置任意放置，传播到最后的层；常规程度上，邻节点被层次的融合在粗化的程度上，池化重新排列图信号；图2展示了整个过程量，这个规律的重排序使得操作更加高效复合并发框架；

 

3相关工作

3.1 图信号处理

图信号处理是搭建信号处理与谱图之间的理论【6，3，21】，谐波与图理论之间的联系，在规则与非规则的结构嵌入生成基础的信息分析操作，我们建议读者参考【31】来了解，标准的卷积、平移、过滤、膨胀、调制与下采样不可直接应用在图中，需要新的数学理论支持保存原有的直觉概念，在文中，【12，8，10】的作者重新看了小波变换图上的操作，进一步提出了金字塔转化【32。27】中，【34】【25】【26】在同时不同程度的重新定于，展示出初始化时概念的丢失，增强定位的原则

3.2 在非欧式空间的cnn

图神经网络框架【29】简化在【20】在欧式空间中设计嵌入每一个顶点使用rnn使用这向量作为分类与回归，通过设置转换函数代替神经网络的递归关系，向量变为s=f(x)=Wx,输出函数为x=g(s,x)=(s-Dx)+x=Lx+x 代替另一个神经网络；利用切比雪夫不等的k参数来达到K层GNN，进行非线性的图池化操作；我们的模型因此可以分析作为多层融合与节点局部操作。

在【11，7】的工作介绍了局部视野减少特征参数的数量，这种思想是基于特征相似的概念，比如是选择限制性的连接数量在连续的层上，然而模型参数的减少通过探索局部概念设想，并未探索固定性特征，比如说没有权重分享策略，【4】的作者使用空间的gcn，使用权重图来定义局部领节点并计算多尺度聚类，进行图的池化操作；包括空间的权重分析然而存在很多挑战，需要选择并有序化领节点，当具体到空间、时间其他的信息 会丢失；

空间CNN生成转换为3Dmesh，是低纬非欧尚空间的类别在【23】提出的，作者使用北极坐标来定于卷积在网格化块上，形成深度框架，容许不同的流行，达到3D识别效果；

第一个谱图cnn的形成在【4】提出，定义为

 

B是三次方样条，后一个是控制点向量，后一种策略是从图中学习图框架，应用在图片识别、文本分类与生物信息上【13】，方法并未取得关注因为其必要的乘法操作；尽管矩阵计算代价，需要拉普拉斯奇异值分解，需要两个乘法O（N的平方）进行前向与后向传播；另外依赖于傅里叶域的平滑，通过样条参数化进行顶点域的定位，其模型并未提供精确度控制，其很重要，我们重复利用这项工作并克服这些现在；

4 数字分析实验

我们参考非参数非定位的过滤器（2）作为非参数，提出的过滤器在（7）在【4】中 样条，切比雪夫过滤器（4），使用Graclus粗化算法在2.2介绍的并非【4】中的样条凝聚方法，目的是比较学习过滤器并非粗化算法；使用下面的术语描述实验详情：

FCk k个隐藏单元的全连接层；Pk 步长为k的池化层；GCk Ck k个特征图的卷积层  使用的激活函数为ReLU 最后使用的是softmax函数回归，损失函数使用cross—entropy  L2正则化，全连接层 最小batches 是S=100

4.1 重访经典cnn在Mnist 数据集

为了验证模型的性能，选择手写体识别数据集分类问题【19】，70000数字图片二维28*28，图模型，建立8-NN的图2-D栅格化图，产生976的顶点（28*28+192个假节点），边3198个，为了标准化，使用K-nn相似图刻画节点之间的的权重

 

数据的完整性检查很重要，有助于提取特征从二维图上，表1展示了模型的性能

 

差异可以解释通过谱过滤器等方向性自然纹理，比如边并不拥有方向，这是一种限制还是有事，取决于具体问题，应该对任何不变形问题进行验证，旋转不变性可以探索：第一 用于数据增强，第二用于学习旋转不变性特征，比如空间转变网络【14】，其他的解释缺乏实验支持，需要调查更好的初始化策略

LENET-5 like 网络结构，超参数来自下面的实验；https://www.tensorflow.org/versions/r0.8/tutorials/mnist/pros；dropoout =0.5 归一化权重5*10^-4,初始化学习率0.03  衰减率0.95  momentum0.9  过滤器为5*5 支持K=25 所有的训练是20 epochs

4.2 文本分类20news

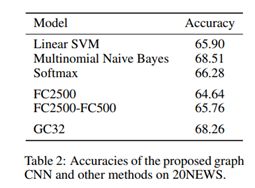
 为了证明模型的通用性，应用在非结构数据上进行文本分类，数据集包含18856数据（11314 train  7532 test）20类的分类【15】，我们提出10000最普遍的词从93953个单词中，每个文本向量x使用词包模型，归一化；本文建立16-nn图 词到向量嵌入的表示【24】，其产生10000个顶点，132834个边，框架是GC32 k=25  表2 是结果，我们的模型并不比贝叶斯分类好在小数据集上，其更强大的性能需要更多的全连接网络

 

 

4.3 比较谱过滤器与计算效率

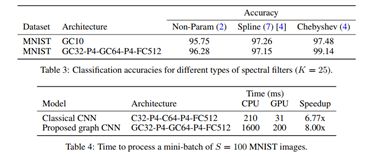
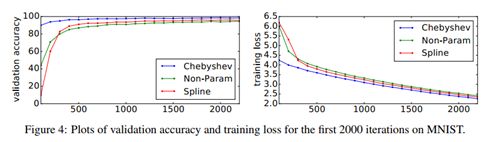
表3 显示了【4】提出参数化模型性能如非参数模型，需要 O（n）级参数。并且图4显示了验证精度与损失；

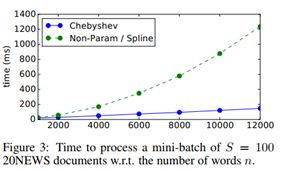
图3验证了模型的低计算复杂度，运行时间等，表4 展示相似的进行GPU运行的情况，展示了并行运算的能力

 

 

 

4.4 图片质量的影响

 

 

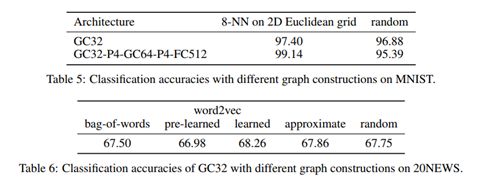
对于任何图，有关数据的局部性、平稳性和组合性的统计假设必须在所在的图上实现，因此学习过滤器的质量取决于图的质量，对于欧式空间的数据，在4.1讨论，展示了K-nn图足够恢复标准CNN的性能。我们注意到K的值并未对性能有较大的影响，我们见证了随机图的性能表现，表5 表达了使用随机图的性能；重要的是数据结构的丢失或者是卷积层不能提出有价值的信息特征

文本分类特征被看为一个词包，调查发现三个选择，每个词都对应着矩阵中的列，另一个方法使用 word2vec[24]嵌入每个词，或者使用预学习嵌入。对于大型数据集 最紧邻节点算法 使用，这就是用 LSHFores【2】在学习word2vec的嵌入，表6 强调框架图的重要性

 

5 结论与未来的工作

在本文中，我们介绍了有效的泛化CNN到使用GSP工具的图的数学与计算基础，实验表明模型抽取局部、平滑与统计特征，通过图卷积层，较于【4】的第一个谱图，更有效率，避免傅里叶基的使用，实验表面了更高的准确率，另外，我们解决了【13】提出的问题，第一 引入线性复杂度的模型，第二证明了图质量对性能的影响 第三验证模型的局部平稳性和合成性统计假设成立

未来的工作有两个方向，提出显得工具，两一方面探索通用模型的使用，可以整合其他数据；另一个方向是方法的合理行，【13】作为先锋的，改变图上的CNN学习的参数；

 

 

 

 

 

 

References
[1] Martín Abadi et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems.
2016.
[2] M. Bawa, T. Condie, and P. Ganesan. LSH Forest: Self-Tuning Indexes for Similarity Search. In International Conference on World Wide Web, pages 651–660, 2005.
[3] M. Belkin and P. Niyogi. Towards a Theoretical Foundation for Laplacian-based Manifold Methods.
Journal of Computer and System Sciences, 74(8):1289–1308, 2008.
[4] J. Bruna, W. Zaremba, A. Szlam, and Y. LeCun. Spectral Networks and Deep Locally Connected Networks on Graphs. arXiv:1312.6203, 2013.
[5] T.N. Bui and C. Jones. Finding Good Approximate Vertex and Edge Partitions is NP-hard. Information
Processing Letters, 42(3):153–159, 1992.
[6] F. R. K. Chung. Spectral Graph Theory, volume 92. American Mathematical Society, 1997.
[7] A. Coates and A.Y. Ng. Selecting Receptive Fields in Deep Networks. In Neural Information Processing
Systems (NIPS), pages 2528–2536, 2011.
[8] R.R. Coifman and S. Lafon. Diffusion Maps. Applied and Computational Harmonic Analysis, 21(1):5–30,
2006.
[9] I. Dhillon, Y. Guan, and B. Kulis. Weighted Graph Cuts Without Eigenvectors: A Multilevel Approach.
IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), 29(11):1944–1957, 2007.
[10] M. Gavish, B. Nadler, and R. Coifman. Multiscale Wavelets on Trees, Graphs and High Dimensional
Data: Theory and Applications to Semi Supervised Learning. In International Conference on Machine
Learning (ICML), pages 367–374, 2010.
[11] K. Gregor and Y. LeCun. Emergence of Complex-like Cells in a Temporal Product Network with Local
Receptive Fields. In arXiv:1006.0448, 2010.
[12] D. Hammond, P. Vandergheynst, and R. Gribonval. Wavelets on Graphs via Spectral Graph Theory.
Applied and Computational Harmonic Analysis, 30(2):129–150, 2011.
[13] M. Henaff, J. Bruna, and Y. LeCun. Deep Convolutional Networks on Graph-Structured Data.
arXiv:1506.05163, 2015.
[14] Max Jaderberg, Karen Simonyan, Andrew Zisserman, et al. Spatial transformer networks. In Advances
in Neural Information Processing Systems, pages 2017–2025, 2015.
[15] T. Joachims. A Probabilistic Analysis of the Rocchio Algorithm with TFIDF for Text Categorization.
Carnegie Mellon University, Computer Science Technical Report, CMU-CS-96-118, 1996.
[16] G. Karypis and V. Kumar. A Fast and High Quality Multilevel Scheme for Partitioning Irregular Graphs.
SIAM Journal on Scientific Computing (SISC), 20(1):359–392, 1998.
[17] D. Kingma and J. Ba. Adam: A Method for Stochastic Optimization. arXiv:1412.6980, 2014.
[18] Y. LeCun, Y. Bengio, and G. Hinton. Deep Learning. Nature, 521(7553):436–444, 2015.
[19] Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner. Gradient-Based Learning Applied to Document Recognition. In Proceedings of the IEEE, 86(11), pages 2278–2324, 1998.
[20] Yujia Li, Daniel Tarlow, Marc Brockschmidt, and Richard Zemel. Gated Graph Sequence Neural Networks.
[21] U. Von Luxburg. A Tutorial on Spectral Clustering. Statistics and Computing, 17(4):395–416, 2007.
[22] S. Mallat. A Wavelet Tour of Signal Processing. Academic press, 1999.
[23] Jonathan Masci, Davide Boscaini, Michael Bronstein, and Pierre Vandergheynst. Geodesic convolutional
neural networks on riemannian manifolds. In Proceedings of the IEEE International Conference on
Computer Vision Workshops, pages 37–45, 2015.
[24] T. Mikolov, K. Chen, G. Corrado, and J. Dean. Estimation of Word Representations in Vector Space. In
International Conference on Learning Representations, 2013.
[25] B. Pasdeloup, R. Alami, V. Gripon, and M. Rabbat. Toward an Uncertainty Principle for Weighted Graphs.
In Signal Processing Conference (EUSIPCO), pages 1496–1500, 2015.
[26] N. Perraudin, B. Ricaud, D. Shuman, and P. Vandergheynst. Global and Local Uncertainty Principles for
Signals on Graphs. arXiv:1603.03030, 2016.
[27] I. Ram, M. Elad, and I. Cohen. Generalized Tree-based Wavelet Transform. IEEE Transactions on Signal
Processing,, 59(9):4199–4209, 2011.
[28] D. Ron, I. Safro, and A. Brandt. Relaxation-based Coarsening and Multiscale Graph Organization. SIAM
Iournal on Multiscale Modeling and Simulation, 9:407–423, 2011.
[29] F. Scarselli, M. Gori, A. C. Tsoi, M. Hagenbuchner, and G. Monfardini. The Graph Neural Network
Model. 20(1):61–80.
[30] J. Shi and J. Malik. Normalized Cuts and Image Segmentation. IEEE Transactions on Pattern Analysis
and Machine Intelligence (PAMI), 22(8):888–905, 2000.
[31] D. Shuman, S. Narang, P. Frossard, A. Ortega, and P. Vandergheynst. The Emerging Field of Signal
Processing on Graphs: Extending High-Dimensional Data Analysis to Networks and other Irregular Domains. IEEE Signal Processing Magazine, 30(3):83–98, 2013.
[32] D.I. Shuman, M.J. Faraji, and P. Vandergheynst. A Multiscale Pyramid Transform for Graph Signals.
IEEE Transactions on Signal Processing, 64(8):2119–2134, 2016.
[33] A. Susnjara, N. Perraudin, D. Kressner, and P. Vandergheynst. Accelerated Filtering on Graphs using
Lanczos Method. preprint arXiv:1509.04537, 2015.
[34] M. Tsitsvero and S. Barbarossa. On the Degrees of Freedom of Signals on Graphs. In Signal Processing
Conference (EUSIPCO), pages 1506–1510, 2015.