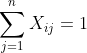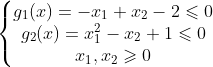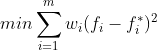利用python求解规划问题

规划问题分为两个大类：线性规划和非线性规划以及下面分支的小类，我们观看这个树状图来粗略的了解一下。

    

首先我们讲解最简单的线性规划模型，通常线性规划均属于凸规划，通常都是用python中的cvxpy进行求解。

线性规划

模型建立由三个部分组成：

（1）决策变量（问题中的未知量，用于表明规划问题中的用数量表示的方案，措施等）

（2）目标函数（是决策变量的函数，通常求该函数的最大值和最小值）

（3）约束条件（决策变量收到的约束和限制条件）

我们直接来看问题

首先我们观察这个约束条件和目标函数，全部都是线性的，所以我们就放心大胆的使用cvxpy

import cvxpy as cp
import numpy as np
s=np.array([[2,4,3],[3,1,5],[7,3,5]])
b=np.array([150,160,200])
a=np.array([70,50,60])
x=cp.Variable(3,pos=True)
obj=cp.Maximize(a@x)
con=[s@x<=b]
prob=cp.Problem(obj,con)
prob.solve(solver='GLPK_MI')
print(x.value)#x的最优解
print(prob.value)#最优值

我们在cvxpy库里是利用Variable函数进行未知量的定义：

x=cp.Variable((m,n),pos=True)

通常我们会定义一个关于x未知量的m行n列的举证，我们在例子中的3也就相当于(1，3).对于后面的 pos=True，当我们对x没有特殊要求时进行这个定义，当我们要对x去整数时要将这个参数改变为 integer=True。当我们需要对定义的函数中的某一个具体函数进行引用时，我们可以用索引的方式将其引用例如 

x[0]+x[1]==5

例子里的obj是我们要求的目标函数，这里我们要求目标函数的最大值所以我们引用函数Maximize(),里面的a@x对应了目标函数，这里的@是矩阵乘法。

而con里面对应的是约束条件，约束条件封装在列表中，每一个约束条件都是列表中的元素。

利用cvxpy求解线性问题我们需要对其封装，然后利用solve函数对其求解，利用Problem(obj，con)对目标函数和约束条件封装。

求解函数solve通常会伴有solver='GLPK_MI'，这里参数的意义指的是不同的求解器，如果你利用这个代码进行求解时，提示'GLPK_MI'没有这个参数，那么说明你并未导入GLPK_MI这个求解器。

这个时候需要安装cvxopt这个库即可。对应不同的问题，我们需要使用不同的求解器。

下面将介绍整数规划

从整数规划的取值范围来看，整数规划通常非为三类：

（1）纯整数规划：所有决策变量都必须取整数值的整数规划模型

（2）混合整数规划：决策变量中一部分取整数值的整数规划值，另一部分可以不取整数值

（3）0-1整数规划：决策变量只能去0或者1的整数规划

前两种并没有的代码部分和上面的例题差不多，但是有0-1整数规划延伸出了一个整数规划的分支，商旅问题又称TSP.

有一个推销员，从城市出发要访遍各一次，最后一次返回。已知从到的旅费为，试问应该怎么走遍这些城市使得，总旅费最小。

这里我们先建立两个矩阵X，和C

矩阵X中的表示从i进入j，如果为真则为1，反之则等于0.

矩阵C中的表示从i进入j的旅费。

其中i=j时，根据题目意思，选择一个充分的大的实数M，这个问题中M=0.

模型建立：

目标函数：（i，j=1，2，，，n）

约束条件：

（1）每个城市只进入一次

,j=1,2,,n

（2）每个城市只离开一次

,i=1,2,,n

（3）防止子回路出现的强制性约束

 (i=1,2,,,n    j=2,3,,,n)

子回路是图论中的一个概念，指的是一个除了一个大的循环外，还有若干个小的循环而这些小的循环就被称为子回路。商旅问题的前两个约束只是必要条件，并不充分，因为如果出现了如下图这种情况，他虽然满足前两个约束条件但是并不构成整体回路。

 所以我们要对其增加第三个约束条件。

关于证明第三个约束条件的可行性：

（1）含有子回路的路线不满足第三个条件

（2）不含回路的整体巡回路线满足这个路线

证明（1）：假如存在子回路，则至少有两个子回路，则至少有一个不含起点V1，就像上图中的第二个图一样，我们把第二个图带入第三个约束条件，则必有：

U4-U5+N<=N-1,U5-U6<=N-1,U6-U4+N<=N-1,

把这三个不等式相加会得到0小于-3，这不可能，所以得证第一个问题。

（2）对于整体巡回路线基本上只要u取值得当。都可以满足这个条件。

针对TSP这类问题。我们通常需要结合图论的知识进行，并且这类知识应用的范围十分广泛，例如模型中的最小资费，也可以放于排队问题当中等等。

非线性规划

下面我们介绍非线性规划：

非线性规划和一般的规划在模型的建立上类似，都含有目标函数，约束条件和决策标量。 在上面的大图中我们能看到，非线性函数被凸函数分为了两类，一类是凸函数规划也称凸规划，另一类则不是凸规划。下面我们来介绍凸函数的定义。

凸函数：

给定的函数,若,有',则称为凸函数。我们对这个概念有印象即可，不必去深入探究，我们需要知道如何判断是否是凸函数。

函数凸性的判断：

（1）充要条件：任意两个不同的点,恒有，通常我们不使用这个条件去判断是否为凸函数。

 (2)充要条件：的Hesse矩阵在上处处半正定（半正定也就是特征值非负）

对于第二个条件对于我们来说不叫便于判断是否为凸函数。因为线性函数既可以看作凸函数，也可以看作凹函数，所线性规划也属于凸规划，而Hesse矩阵是指函数对各个变量的二阶偏导函数。

通常我们不必对线函数进行判断，只需要对式子中的非线性函数进行判断。对于非线性问题，若是凸函数，而为R上的凸函数，为R上的线性函数时，称该非线性规划问题为凸规划。

例如：

对于这个非线性规划，我们需要判断和是否为凸函数。

import numpy as np
import sympy as sp
from numpy.linalg import eigvals
n=2
X=sp.var('x1,x2')
e=np.random.randint(0,3,(n,n))
Y=x1**2+x2**2-4*x1+4
for i in range(n):
     Y1=Y.diff(X[i])
     for j in range(n):
         Y2=Y1.diff(X[j])
         e[i,j] = Y2
T=eigvals(e)
for i in range(len(T)):
     if T[i]>=0 :
          if i==len(T)-1:
               print('是凸函数')
          continue
     else:
          print('不是凸函数')
          break

这个代码就可以判断大多数方程是否是凸函数。通过对方程的判断，我们发现这个规划是一个凸规划，所以我们可以使用cvxpy库的方法进行求解。

import cvxpy as cp
x=cp.Variable(2,pos=True)
obj=cp.Minimize(x[0]**2+x[1] ** 2-4*x[0]+4)
con=[-x[0]+x[1]-2<=0,x[0]**2-x[1]+1<=0]
prob=cp.Problem(obj,con)
prob.solve(solver='CVXOPT')
print(prob.value)
print(x.value)

这个代码和第一个有略微不同，这里使用了新的求解器——CVXOPT，也可以自己尝试一下用之前的求解器，但是会报错原因是'GLPK_MI'无法求解这个问题，所以会报错。如果使用求解器——CVXOPT，依旧报错可能是你并未安装这个求解器。

当我们判断其不是凸规划时，我们就不能使用CVXPY库进行求解，这里我们应该使用minimize函数，或者使用sympy库进行求解。对于非线性问题又可以分为有约束，和无约束两种情况。我们先介绍无约束非线性规划。

无约束

在同济版的高等数学（111~116）有介绍如何求二元函数极值的方法，可以平行推广到无约束问题。设有连续的一阶偏导数，且是无约束问题的局部极小点，那么就有,这里是函数的梯度。当函数有连续的二阶偏导数，且为正定矩阵时，是此规划问题局部最优解。

简单介绍一下梯度的概念：函数在某一点的梯度是这样一个向量，它的方向与取得最大方向导数的方向一致，而它的模为方向导数的最大值。对于二元函数来说它的梯度,具体内容可见同济版的高等数学（106~111）

 求解无约束问题困难的是求解，常用的方法有最速降解法，牛顿法等等。我们简单介绍一个二元函数非线性问题求解的小例子：

对于此类问题我们采用sympy库进行求解

import sympy as sp
sp.var('x1,x2')
Y=-0.01*x1**2+-0.007*x1*x2-0.01*x2**2+144*x1+174*x2-400000
y1=Y.diff(x1)
y2=Y.diff(x2)
s=sp.solve([y1,y2],[x1,x2])
x3=s[x1]
x4=s[x2]
y0=Y.subs({x1:x3,x2:x4})
print(y0)

这样就能求出最优解，其中diff函数是求导函数，subs函数可以将x的值代入方程从而得到最优解，这里利用了二元函数求导的方法，关于其他函数。在我的sympy简介里有相关介绍。

有约束

在实际中，绝大多数问题都是有约束问题。我们在面对有约束的非线性规划问题时，没有适用于各种问题的一般算法，各种算法都有其特定的适用范围，且具有一定局限性。

所幸我们并不需要去具体了解各种算法，python的minimize函数可以为我们解决这个问题，当非线性规划是凸规划时，我们可以继续适用cvxpy库，但当其不是凸规划时，我们就必须使用minimize函数了。

例如 

首先我们判断这是否是个凸规划，判断后明显不是。所以我们使用minimize函数

import numpy as np
from  scipy.optimize import  minimize
c=np.array([[-1,-0.15],[-0.15,-1]])
a=np.array([98,277])
obj=lambda x:x@c@x+x@a
b=np.array([100,0])
con={'type':'ineq','fun':lambda x:b-a@x}
bd=[(0,np.inf) for x in range(2)]
res=minimize(obj,np.random.randn(2),constraints=con,bounds=bd)
print(res)

下面我们介绍详细函数的概念：

这里个人理解的一般，但是为大家找到了，较为详细的讲解。http://t.csdn.cn/1379W

仔细观察这个规划的目标函数，细心的小伙伴可以发现这是一个二次函数（在线性代数里有具体的讲解）。

对于这种目标函数，并且约束条件都是线性的，那么我们称这个模型为二次规划(QP)，当目标函数写成矩阵形式时，当此矩阵正定时，目标函数最小化，模型为凸二次规划，则此时局部最优解就是全局最优解。

多目标规划

在实际生活中，我们可能不仅要一个目标最优，可能涉及到多个目标最优化，例如工厂在生产时，需要兼顾利润最大化和污染最小化，这就是多目标规划，下面介绍几种常用的方法。

在求解之前我们通常需要对目标进行预处理，包括：（1）无量化纲处理（2）归一化处理

（1）线性加权法

基本思想：根据目标的重要程度确定权重，以目标函数的加权平均值为评价函数，使其达到最优。也就是各权重各目标函数，作为一个目标函数。

 ,是权重，是目标函数。

（2）约束法

基本思想：根据决策者偏好，选择一个主要关注的参考目标，然后将其他目标函数放到约束条件中。

,,这其中的参数都是决策者事先给出的。

约束法又叫主目标法或者参考目标法，参数是决策者对当前目标能会接受的限度值。

（3）理想点法

基本思想：以每个单目标最优值为该目标的理想值，使每个目标函数值与理想值的差的加权平方和最小。

第一：首先求出每个目标函数的理想值。以单个目标函数为目标构造单目标规划，求此规划最优值。

第二：构造每个目标函数和理想值的差的加权平方和，做出评价函数。

权重通常经过归一化处理，即权重和为一。

第三：求出评价函数的最优值。

求解m+1个单目标规划。

（4）优先级法

基本思想：根据目标的重要性分成不同优先级，先求优先级高的目标函数的优先级，确保优先级高的目标函数的最优值，确保优先级高的目标获得的值不低于最优值，再求优先级低的目标函数。

第一:确定优先级

第二：求第一级单目标最优值

第三步：以第一级单目标等于最优值为约束，求第二优先级的目标最优。当求出第二优先级的最优值时，在以第一，第二最优值为条件，计算第三目标，以此类推。