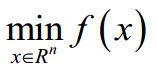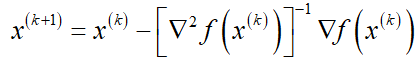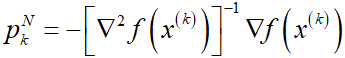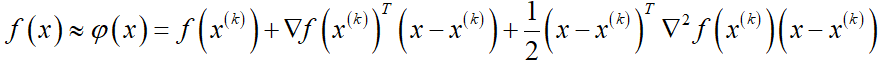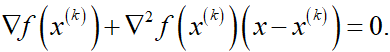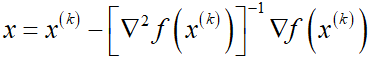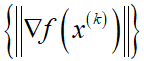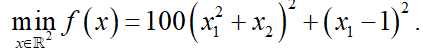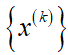牛顿下山法matlab_优化算法之牛顿法
牛顿法(Newton's method)是一种在实数域和复数域上近似求解方程的方法,，它使用函数f(x)的泰勒级数的前面几项来寻找方程f(y)=0的根。 牛顿法最初由艾萨克·牛顿在《Method of Fluxions》(1671年完成，1736年公开发表)中提出。约瑟夫·鲍易也曾于1690年在Analysis Aequationum中提出此方法。
目录
1问题提出1. 问题提出
2. 基本思想
3. 迭代公式
4. 算法步骤
5. 算法收敛性
6. 解的情况
7. 阻尼牛顿法
8. 算法实现
9. 算法评价
对于无约束优化模型
其中
为二阶连续光滑且Hessian阵可逆。
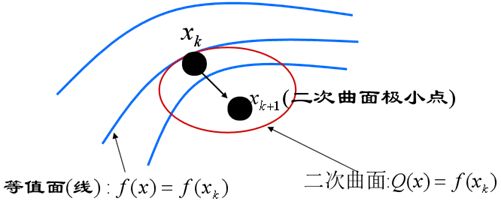
用一个二次函数去近似目标函数f(x),然后精确地求出这个二次函数的极小点.
Newton法几何解释
3迭代公式Newton法的迭代公式为：
其中
称为牛顿方向。
考虑函数f(x)在点
处的二次泰勒近似
由于
可逆，则
的一阶稳定点满足
，即
由上式可得
这正是牛顿法的迭代公式。由此说明，牛顿法在每次迭代中考虑函数在当前的局部二次泰勒展开，其迭代步长为1，迭代方向是梯度方向经过Hessian逆阵的调整。如果函数f为凸函数，此时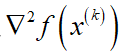正定，从而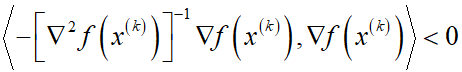
,即牛顿方向是下降方向。
牛顿法的算法步骤如下：
Step 0. 选取初始点
，允许误差ε> 0，令 k=1；
Step 1. 计算
。若
,算法停止；.否则，转 Step 2；
Step 2. 计算
。置k=k+1，转 step 1.
这里讨论牛顿算法的局部收敛性质，这是由于Hessian阵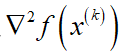可能不总是正定，即
牛顿方向可能不总是下降方向。我们假设目标函数f为凸函数，二阶连续可微，最优解
处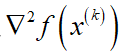正定。此时，在附近的点，其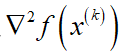也是正定的。从而牛顿方法是有定义的，并且在迭代步长最终取1的情况下具有二次收敛性。
定理：假设函数f二阶可微，其Hessian阵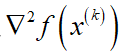在最优解的邻域是Lipschitz连续的，且在处满足充分条件
且
正定。考虑迭代公式
，则下面结论成立：
(i)如果初始点充分接近解点,算法产生的点列
收敛到;
(ii)点列收敛速率是二次的；
(iii)梯度模长的点列
二次收敛到0.
用Newton法求解无约束问题会出现以下情形：
算法收敛到极小点；
算法收敛到鞍点；
Hesse矩阵不可逆，无法迭代下去。
牛顿法的有效性严重依赖初始点的选择，即初始点需要充分靠近极小值点，否则可能导致算法不收敛。由于实际问题的精确最小值点一般是不知道的，因此初始点的选择给算法的实现带来了很大的挑战。为了解决这一问题，可引入线搜索技术以得到大范围的收敛算法，即阻尼牛顿法。
阻尼牛顿法的算法步骤如下：
Step 0. 选取初始点，允许误差ε> 0，令 k=1；
Step 1. 计算。若,算法停止；.否则，转 Step 2；
Step 2. 取搜索方向
，利用线搜索技术确定步长
;
Step 3. 令
。置k=k+1，转 step 1.
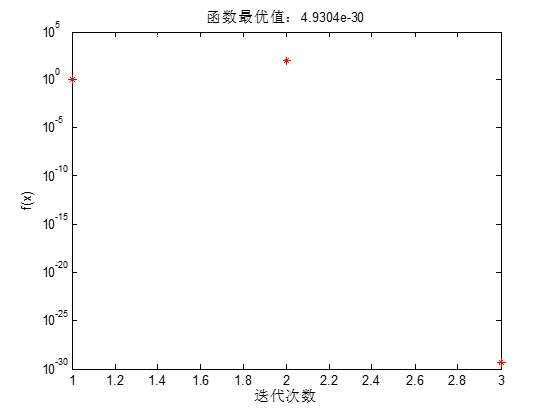
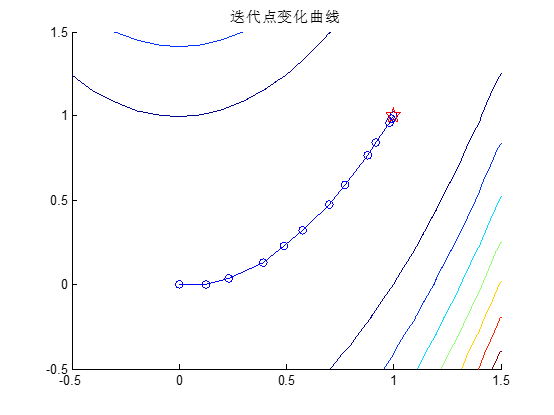
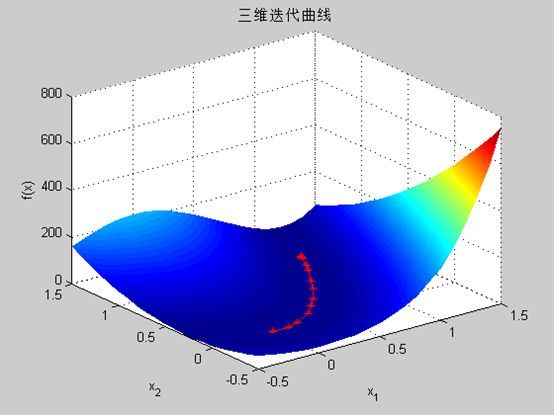
例1：求解无约束优化问题
该问题有精确解
解：
方法1：牛顿法法
使用 MATLAB 编写最速下降法的主函数如下：
function [X,Y,Error] = Newton(x0)
%使用牛顿法求解无约束问题：min f(x)
%输入：x0为初始点，fun为目标函数，grad为梯度函数
%输出:X,Y分别为每一步的迭代点及相应函数值，Error为误差
tic
%% 定义目标函数及导函数信息(可以根据需要进行修改)
f = @(x)100*(x(1)^2-x(2))^2+(x(1)-1)^2; %目标函数
g = @(x)[400*x(1)*(x(1)^2-x(2))+2*(x(1)-1);-200*(x(1)^2-x(2))]; %一阶导数
G = @(x)[1200*x(1)^2-400*x(2)+2,-400*x(1);-400*x(1), 200 ]; %二阶导数
%% 初始化算法参数
n = 1;
e = norm(g(x0));
X = x0;
Y = f(x0);
Error = e;
%% 设定终止条件
N = 5000; %最大迭代步
E = 1e-6; %给定误差
%% 迭代
while n < N && e > E
n = n+1;
%判断Hesse矩阵是否可逆
ifdet(G(x0)) == 0
disp('Hesse矩阵不可逆，无法进行迭代！');
break
else
d =-inv(G(x0))*g(x0); %迭代方向
x0 =x0+d; %迭代公式
X(:,n)= x0;
Y(n) =f(x0);
e =norm(g(x0));
Error(n) = e;
end
end
toc
end
调用格式如下：
x0 = [0;0]; %迭代初始点(可以根据需要修改)
[X,Y,E]=Newton(x0);
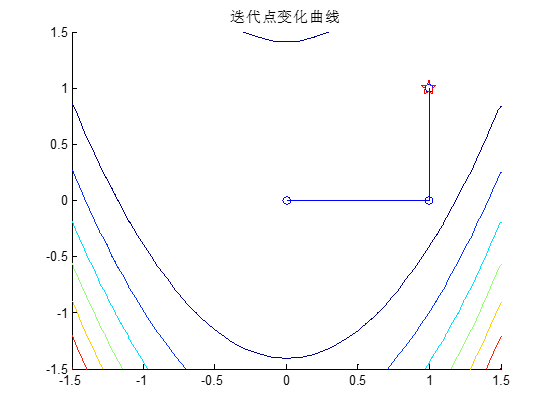
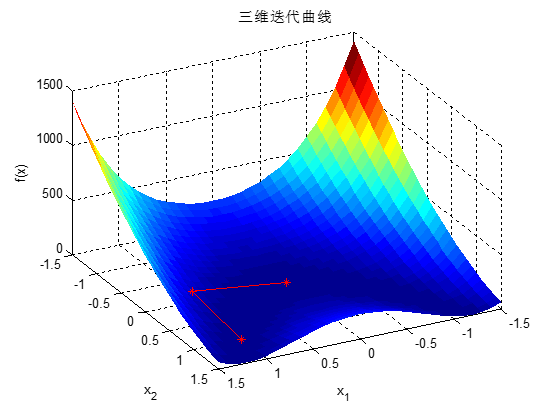
本问题求解结果如下：
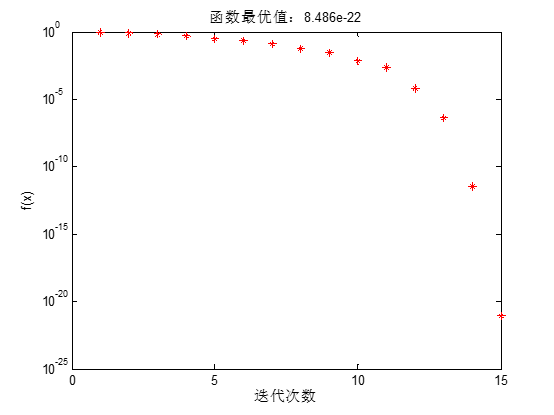
方法2：阻尼牛顿法
使用 MATLAB 编写最速下降法的主函数如下：
function [X,Y,Error] =ZNNewton(x0)
%使用阻尼牛顿法求解无约束问题：min f(x)
%使用非精确Armijo搜索步长规则
%输入：x0为初始点，fun为目标函数，grad为梯度函数
%输出:X,Y分别为每一步的迭代点及相应函数值，Error为误差
tic
%% 初始化参数
f = @(x)100*(x(1)^2-x(2))^2+(x(1)-1)^2; %目标函数
g =@(x)[400*x(1)*(x(1)^2-x(2))+2*(x(1)-1);-200*(x(1)^2-x(2))]; %一阶导数
G =@(x)[1200*x(1)^2-400*x(2)+2, -400*x(1);-400*x(1), 200 ]; %二阶导数
%% 初始化算法参数
n = 1;
e = norm(g(x0));
X = x0;
Y = f(x0);
Error = e;
beta=0.5;sigma=0.4;
%% 设定终止条件
N = 5000; %最大迭代步
E = 1e-6; %给定误差
%% 迭代
while n < N &&e > E
n = n+1;
%判断Hesse矩阵是否可逆
if det(G(x0)) == 0
disp('Hesse矩阵不可逆，无法进行迭代！');
break
else
d = -inv(G(x0))*g(x0); %迭代方向
%使用Armijo法求步长
m=0; mk=0;
while(m<20)
if(f(x0+beta^m*d)
mk=m; break;
end
m=m+1;
end
x0 = x0+beta^mk*d; %迭代公式
X(:,n) = x0;
Y(n) = f(x0);
e = norm(g(x0));
Error(n) = e;
end
end
toc
end
调用格式如下：
x0 = [0;0]; %迭代初始点(可以根据需要修改)
[X,Y,E]=ZNNewton(x0);
本问题求解结果如下：
1)优点:
Newton法产生的点列
若收敛，则收敛速度快---具有至少二阶收敛速率；Newton法具有二次终止性，即对强凸函数Newton法只需迭代一次就能得到最优值。
2)缺点:
Newton法可能会出现在某步迭代时，目标函数值上升；
当初始点远离极小点时，Newton法产生的点列可能不收敛，或者收敛到鞍点，或者Hesse矩阵不可逆，无法计算；
Newton法需要计算Hesse矩阵，计算量大.
往期回顾
算法丨优化算法之最速下降法
算法丨经典优化算法大合集(比赛备用，值得收藏)
算法丨优化算法系列之遗传算法原理
算法丨优化算法系列之遗传算法MATLAB程序设计及应用实例
算法丨优化算法系列之模拟退火算法(1)
算法丨优化算法系列之模拟退火算法(2)——0-1背包问题
参考文献：马昌凤.最优化方法及其 Matlab 程序设计[M]. 科学出版社, 2010.
