24 - 从向量内积角度逐行实现PyTorch二维卷积完整版

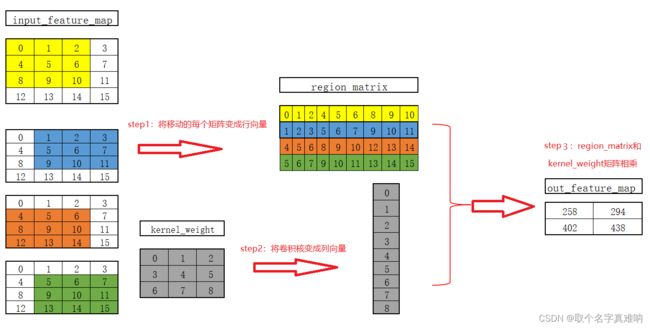
1. 图示思路

2. 代码

• 重点函数

# 自定义一个矩阵滑动的卷积函数，这里只做二维矩阵和二维矩阵的卷积计算
def matrix_multiplication_for_conv2d(input, kernel, stride=1, padding=0, bias=0):

• 整体代码

import torch
from torch import nn
from torch.nn import functional as F
import math

# 定义输入的矩阵
input_feature_map = torch.arange(16, dtype=torch.float).reshape((1, 1, 4, 4))
# 定义输入通道为1
in_channel = 1
# 定义输出通道为1
out_channel = 1
# 定义卷积核大小
kernel_size = 3
# 定义卷积核的权重值；kernel_weight.shape = torch.Size([out_channel,in_channel,kernel_height,kernel_width])
kernel_weight = torch.arange(9, dtype=torch.float).reshape(1, 1, 3, 3)
# 通过Conv2d类实例化一个卷积核
my_conv2d = nn.Conv2d(in_channels=in_channel, out_channels=out_channel, kernel_size=kernel_size, bias=False)
# 将卷积核的权重赋值
my_conv2d.weight = nn.Parameter(kernel_weight, requires_grad=True)
# 得到输出特征矩阵，此时用的是nn.Conv2d类处理
output_feature_map = my_conv2d(input_feature_map)
# 得到输出特征矩阵，此时用的是F.conv2d方法处理
functional_output_feature_map = F.conv2d(input_feature_map, kernel_weight)
print(f"input_feature_map={input_feature_map}")
print(f"input_feature_map.shape={input_feature_map.shape}")
print(f"my_conv2d.weight={my_conv2d.weight}")
print(f"my_conv2d.weight.shape={my_conv2d.weight.shape}")
print(f"output_feature_map={output_feature_map}")
print(f"output_feature_map.shape={output_feature_map.shape}")
print(f"functional_output_feature_map={functional_output_feature_map}")
print(f"functional_output_feature_map.shape={functional_output_feature_map.shape}")

# 定义输入矩阵
my_input_matrix = torch.arange(16, dtype=torch.float).reshape(4, 4)
# 定义卷积核矩阵
my_kernel = torch.arange(9, dtype=torch.float).reshape(3, 3)


# 自定义一个矩阵滑动的卷积函数，这里只做二维矩阵和二维矩阵的卷积计算
def matrix_multiplication_for_conv2d(input, kernel, stride=1, padding=0, bias=0):
	# 判断是否需要填充，如果需要，就将上下左右都进行填充指定padding行
	if padding > 0:
		input = F.pad(input, (padding, padding, padding, padding))
	# 得到填充后矩阵的高宽
	input_h, input_w = input.shape
	# 得到卷积核的高宽
	kernel_h, kernel_w = kernel.shape
	# 得到输出矩阵高宽
	output_h = math.floor((input_h - kernel_h) / stride + 1)
	output_w = math.floor((input_w - kernel_w) / stride + 1)
	# 生成一个全0大小的输出矩阵
	output_matrix = torch.zeros(output_h, output_w)
	# 开始遍历，先得到遍历坐标
	for i in range(0, input_h - kernel_h + 1, stride):
		for j in range(0, input_w - kernel_w + 1, stride):
			# 获取遍历的区间region
			region = input[i:i + kernel_h, j: j + kernel_w]
			# 点积后求和得到相应的值
			output_matrix[int(i / stride), int(j / stride)] = torch.sum(region * kernel) + bias

	return output_matrix


# 根据自定义的卷积函数求出输出矩阵
my_output = matrix_multiplication_for_conv2d(my_input_matrix, my_kernel)
# 打印输出结果
print(f"my_output={my_output}")
print(f"判断自定义函数得到的结果是否跟pytorch计算结果一致\n{torch.isclose(my_output, torch.squeeze(functional_output_feature_map))}")
my_input_new = torch.randn(5, 5)
my_kernel_weight = torch.randn(3, 3)
my_kernel_bias = torch.randn(1)
my_ouput_new = torch.squeeze(F.conv2d(my_input_new.reshape(1, 1, 5, 5), weight=my_kernel_weight.reshape(1, 1, 3, 3),
									  bias=my_kernel_bias, stride=2, padding=2))
my_ouput_fun = matrix_multiplication_for_conv2d(my_input_new, my_kernel_weight, stride=2, padding=2,
												bias=my_kernel_bias)
print(f"my_ouput_new={my_ouput_new}")
print(f"my_ouput_fun={my_ouput_fun}")
print(torch.isclose(my_ouput_new, my_ouput_fun))



def matrix_multiplication_for_flatten(input, kernel, stride=1, padding=0, bias=0):
	# 判断是否需要填充，如果需要，就将上下左右都进行填充指定padding行
	if padding > 0:
		input = F.pad(input, (padding, padding, padding, padding))
	# 得到填充后矩阵的高宽
	input_h, input_w = input.shape
	# 得到卷积核的高宽
	kernel_h, kernel_w = kernel.shape
	# 得到输出矩阵高宽
	output_h = math.floor((input_h - kernel_h) / stride + 1)
	output_w = math.floor((input_w - kernel_w) / stride + 1)
	# 生成一个全0大小的输出矩阵
	output_matrix = torch.zeros(output_h, output_w)
	# 将核矩阵转换成列向量
	kernel_vector = kernel.reshape((kernel.numel(), 1))
	# 创建一个region_matrix 将提取到的区间转换成一行一行堆叠起来的矩阵
	region_matrix = torch.zeros(output_matrix.numel(), kernel.numel())
	row_index = 0
	for i in range(0, input_h - kernel_h + 1, stride):
		for j in range(0, input_w - kernel_w + 1, stride):
			# 获取遍历的区间region
			region = input[i:i + kernel_h, j: j + kernel_w]
			# 点积后求和得到相应的值
			region_vector = torch.flatten(region)
			region_matrix[row_index] = region_vector
			row_index += 1
	# 将堆叠后的矩阵和卷积核列向量进行矩阵相乘
	output_matrix = region_matrix @ kernel_vector
	# 将矩阵恢复到需要的形状
	output_matrix = output_matrix.reshape((output_h,output_w))
	return output_matrix


output_flatten = matrix_multiplication_for_flatten(my_input_matrix, my_kernel)
print(f"output_flatten={output_flatten}")
print(f"output_flatten.shape={output_flatten.shape}")
print(f"my_output={my_output}")
print(f"判断矩阵是否一致：\n"
	  f"output_flatten,my_output)\n{torch.isclose(output_flatten,my_output)}")

input_feature_map=tensor([[[[ 0.,  1.,  2.,  3.],
          [ 4.,  5.,  6.,  7.],
          [ 8.,  9., 10., 11.],
          [12., 13., 14., 15.]]]])
input_feature_map.shape=torch.Size([1, 1, 4, 4])
my_conv2d.weight=Parameter containing:
tensor([[[[0., 1., 2.],
          [3., 4., 5.],
          [6., 7., 8.]]]], requires_grad=True)
my_conv2d.weight.shape=torch.Size([1, 1, 3, 3])
output_feature_map=tensor([[[[258., 294.],
          [402., 438.]]]], grad_fn=<ThnnConv2DBackward>)
output_feature_map.shape=torch.Size([1, 1, 2, 2])
functional_output_feature_map=tensor([[[[258., 294.],
          [402., 438.]]]])
functional_output_feature_map.shape=torch.Size([1, 1, 2, 2])
my_output=tensor([[258., 294.],
        [402., 438.]])
判断自定义函数得到的结果是否跟pytorch计算结果一致
tensor([[True, True],
        [True, True]])
my_ouput_new=tensor([[ 3.2830e-01,  2.7485e+00,  1.9194e+00,  2.8474e+00],
        [-1.1993e+00, -2.2748e+00,  7.3436e+00, -2.1672e+00],
        [ 7.4937e-01,  6.2679e+00,  1.3324e+00, -4.9498e-03],
        [ 1.6167e-01,  1.0183e+00, -6.7516e-01,  6.6955e-01]])
my_ouput_fun=tensor([[ 3.2830e-01,  2.7485e+00,  1.9194e+00,  2.8474e+00],
        [-1.1993e+00, -2.2748e+00,  7.3436e+00, -2.1672e+00],
        [ 7.4937e-01,  6.2679e+00,  1.3324e+00, -4.9498e-03],
        [ 1.6167e-01,  1.0183e+00, -6.7516e-01,  6.6955e-01]])
tensor([[True, True, True, True],
        [True, True, True, True],
        [True, True, True, True],
        [True, True, True, True]])
output_flatten=tensor([[258., 294.],
        [402., 438.]])
output_flatten.shape=torch.Size([2, 2])
my_output=tensor([[258., 294.],
        [402., 438.]])
判断矩阵是否一致：
output_flatten,my_output)
tensor([[True, True],
        [True, True]])

3. torch.nn.unfold

通过滑动来实现卷积中的“卷”;不用实现积;
注意行数为卷积核元素个数，列数为卷积核个数

• 代码

# -*- coding: utf-8 -*-
# @Project: zc
# @Author: zc
# @File name: unflod_test
# @Create time: 2022/4/6 7:57
import torch
from torch import nn
from torch.nn import functional as F
import math


# 
def matrix_multiplication_for_flatten(input, kernel, stride=1, padding=0, bias=0):
	# 判断是否需要填充，如果需要，就将上下左右都进行填充指定padding行
	if padding > 0:
		input = F.pad(input, (padding, padding, padding, padding))
	# 得到填充后矩阵的高宽
	input_h, input_w = input.shape
	# 得到卷积核的高宽
	kernel_h, kernel_w = kernel.shape
	# 得到输出矩阵高宽
	output_h = math.floor((input_h - kernel_h) / stride + 1)
	output_w = math.floor((input_w - kernel_w) / stride + 1)
	# 生成一个全0大小的输出矩阵
	output_matrix = torch.zeros(output_h, output_w)
	# 将核矩阵转换成列向量
	kernel_vector = kernel.reshape((kernel.numel(), 1))
	# 创建一个region_matrix 将提取到的区间转换成一行一行堆叠起来的矩阵
	region_matrix = torch.zeros(output_matrix.numel(), kernel.numel())
	row_index = 0
	for i in range(0, input_h - kernel_h + 1, stride):
		for j in range(0, input_w - kernel_w + 1, stride):
			# 获取遍历的区间region
			region = input[i:i + kernel_h, j: j + kernel_w]
			# 点积后求和得到相应的值
			region_vector = torch.flatten(region)
			region_matrix[row_index] = region_vector
			row_index += 1

	return region_matrix.T

input1 = torch.arange(16,dtype=torch.float).reshape((4,4))
kernel1 = torch.arange(9,dtype=torch.float).reshape((3,3))

# 手动实现卷操作
output1 = matrix_multiplication_for_flatten(input1,kernel1)
print(f"input1={input1}")
print(f"kernel1={kernel1}")
print(f"output1={output1}")

# 调用pytorch.nn.Unfold操作实现卷
my_unfold = nn.Unfold(kernel_size=(3,3))
my_input = input1.unsqueeze(0).unsqueeze(0)
my_ouput_unfold = my_unfold(my_input).squeeze()
print(f"my_input={my_input.shape}")
print(f"my_ouput_unfold={my_ouput_unfold}")
print(f"my_ouput_unfold.shape={my_ouput_unfold.shape}")


print(f"my_input={my_input}")
print(f"my_input.shape={my_input.shape}")
print(f"kernel_size=(3,3)")
func_unfold = F.unfold(my_input,kernel_size=(3,3))
print(f"func_unfold={func_unfold}")
print(f"func_unfold.shape={func_unfold.shape}")

• 结果：

input1=tensor(
	   [[ 0.,  1.,  2.,  3.],
        [ 4.,  5.,  6.,  7.],
        [ 8.,  9., 10., 11.],
        [12., 13., 14., 15.]])
kernel1=tensor(
	   [[0., 1., 2.],
        [3., 4., 5.],
        [6., 7., 8.]])
output1=tensor(
       [[ 0.,  1.,  4.,  5.],
        [ 1.,  2.,  5.,  6.],
        [ 2.,  3.,  6.,  7.],
        [ 4.,  5.,  8.,  9.],
        [ 5.,  6.,  9., 10.],
        [ 6.,  7., 10., 11.],
        [ 8.,  9., 12., 13.],
        [ 9., 10., 13., 14.],
        [10., 11., 14., 15.]])
my_input=torch.Size([1, 1, 4, 4])
my_ouput_unfold=tensor(
	   [[ 0.,  1.,  4.,  5.],
        [ 1.,  2.,  5.,  6.],
        [ 2.,  3.,  6.,  7.],
        [ 4.,  5.,  8.,  9.],
        [ 5.,  6.,  9., 10.],
        [ 6.,  7., 10., 11.],
        [ 8.,  9., 12., 13.],
        [ 9., 10., 13., 14.],
        [10., 11., 14., 15.]])
my_ouput_unfold.shape=torch.Size([9, 4])
my_input=tensor(
       [[[[ 0.,  1.,  2.,  3.],
          [ 4.,  5.,  6.,  7.],
          [ 8.,  9., 10., 11.],
          [12., 13., 14., 15.]]]])
my_input.shape=torch.Size([1, 1, 4, 4])
kernel_size=(3,3)
func_unfold=tensor(
	   [[[ 0.,  1.,  4.,  5.],
         [ 1.,  2.,  5.,  6.],
         [ 2.,  3.,  6.,  7.],
         [ 4.,  5.,  8.,  9.],
         [ 5.,  6.,  9., 10.],
         [ 6.,  7., 10., 11.],
         [ 8.,  9., 12., 13.],
         [ 9., 10., 13., 14.],
         [10., 11., 14., 15.]]])
func_unfold.shape=torch.Size([1, 9, 4])