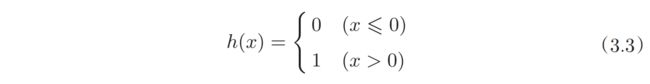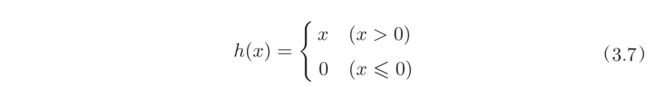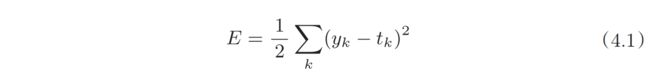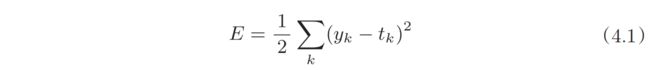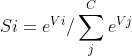《深度学习入门-基于Python的理论与实现》读书笔记

写在前面：

1、该读书笔记将侧重总结深度学习理论而非Python实现。

2、本书环境基于Python3.x+Numpy+Matplotlib。

目录

第一章 Python入门

第二章 感知机

第三章 神经网络

第四章 神经网络的学习

第五章 误差反向传播法

第六章 与学习相关的技巧

 第七章 卷积神经网络

卷积层

通道方向上有多个特征图

通道方向上有多个滤波器

激活函数层

Sigmoid

ReLU（Rectified Linear Unit，修正线性单元）

Softmax

池化层

Dropout层

BN层

全连接层

第八章 深度学习

---

---

第一章 Python入门

第二章 感知机

第三章 神经网络

        最简单的神经网络有一个输入层一个输出层和一个中间层（隐藏层）组成，复杂的神经网络可以包含多层中间层。

        神经网络与感知机（人类大脑的神经元）类似，神经元接受输入信息，判断是否激活该神经元，然后根据某种处理方式得到结果输出。拆解神经网络的一个节点可以发现，它是由输入x1、x2，1，偏置b，权重w1、w2，激活函数h()和输出y组成的。

        具体公式可以如下表示，其中偏置表示该神经元被激活的难易度，激活函数h()则表示该神经元的处理方式。

 

         最简单的激活函数是阶跃函数。

        常用的激活函数包括sigmoid函数和ReLu函数 

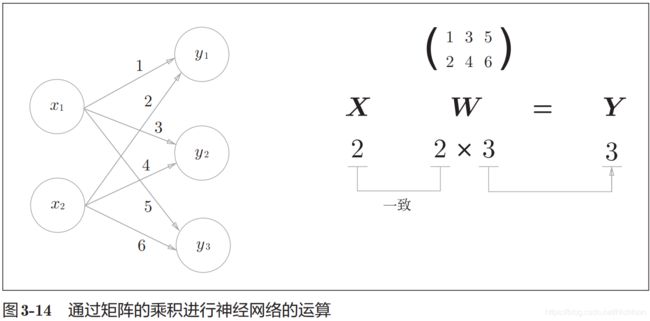
        神经网络的运算主要为大量的矩阵运算，注意各数据的维度要保持一致，输出的维度又权重的列数决定。

         输出层的激活函数与前几层稍有不同，通常神经网络可以用在分类问题（数据属于哪一个类别）和回归问题（根据某个输入预测一个（连续的）数值）上，一般来说，分类问题用softmax函数，回归问题用恒等函数。

        恒等函数将输入按原样输出，不做任何改动；softmax函数可以用以下式子表示，使用softmax函数可以用概率的方法处理问题。

         使用神经网络解决问题时，需要先使用训练数据进行权重参数的学习；进行推理时，使用刚才学习到的参数，对输入数据进行分类。

 第四章 神经网络的学习

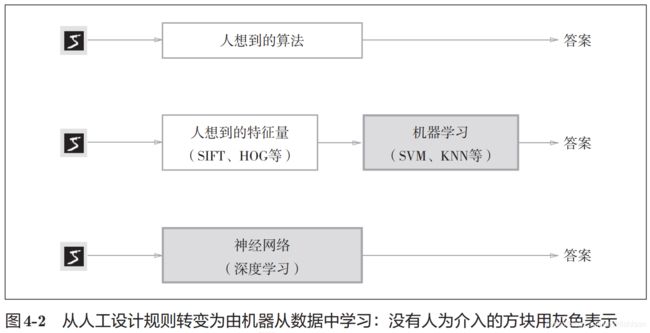
         首先需要提取特征量，这里比较以下传统方法、机器学习和神经网络的区别。

         机器学习中，一般将数据分为训练数据和测试数据，训练数据用来寻找最优参数，然后使用测试数据评价模型的泛化能力，泛化能力是指处理未被观察过的数据的能力，获得泛化能力是机器学习的最终目标。

        寻找最优参数即寻找使损失函数的值最小的参数，因此需要先定义损失函数，最常用的是均方根误差，其中y表示神经网络的输出，t表示监督数据，k表示数据维数。

         其他还有交叉熵误差等。

         注意不能使用识别精度为指标，因为需要输出值是连续的，否则参数的导数在绝大多数地方都会变成0，因此阶跃函数不能作为激活函数，否则输出都会变成不连续的，而sigmoid函数的导数在任何地方都不为0，这对神经网络的学习非常重要。

        注：batch是批处理的意思，batch_size=100表示将100张图同一批次处理。

 第五章 误差反向传播法

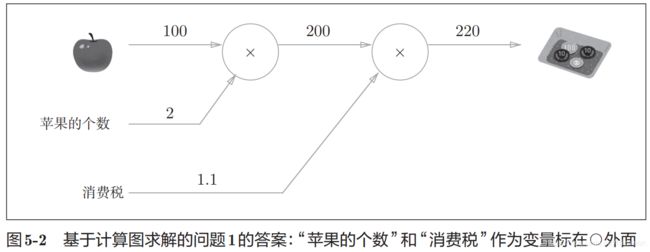
        有数据式和计算图两种方法，计算图将计算过程用图形表示出来，比较直观，本章以计算图为例。

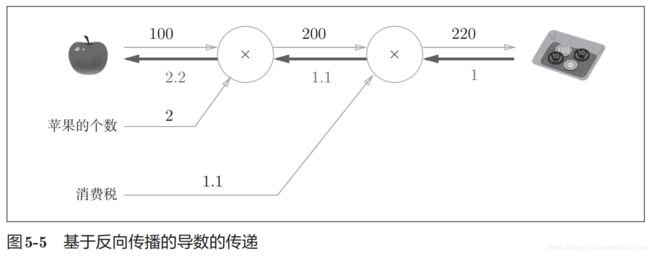
        苹果价格100日元，个数2个，消费税10%，最后实付220日元。

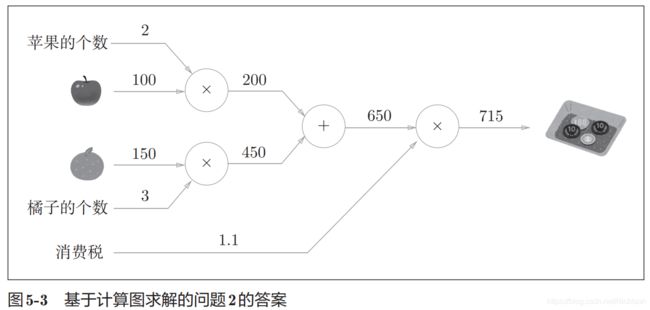
         加上另一种水果后如下。

           用计算图解决问题的步骤是先构建计算图，然后从左到右计算。其中这个从左到右的计算过程是一种正方向的传播，简称正向传播，获得了正向传播结果后，可以通过导数计算实现反向传播。

  

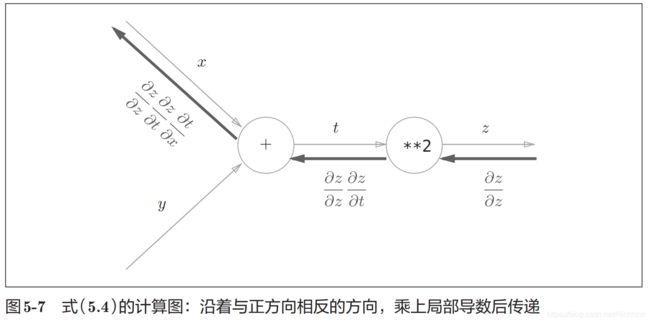
         反向传播的计算顺序是，先将节点的输入信号乘以节点的局部导数(偏导数)，然后再传递给下一个节点。比如反向传播时，“**2”节点的输入是z对z的偏导数，将其乘以局部导数即z对t的偏导数（因为正向传播是，输入是t、输出是z，所以这个节点的偏导数是z对t的偏导数），然后传播给下一个节点。注意反向传播第一个节点的输入是1；从图上的公式可以看出反向传播符合链式法则，即一个节点的输入累乘上这个节点的偏导数就等于这个节点的输出。

第六章 与学习相关的技巧

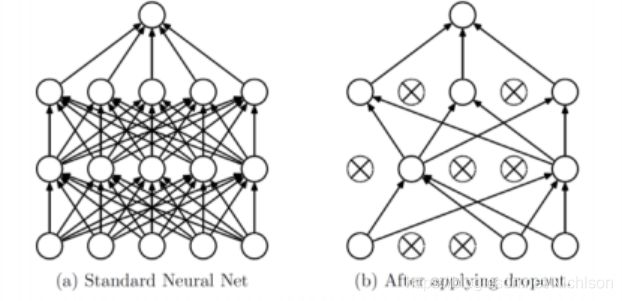
        Dropout是一种在学习过程中随机删除神经元的方法。训练时，随机选出隐藏层的神经元，然后将其删除。被删除的神经元不再进行信号的传递。训练时，每传递一次数据，就会随机选择要删除的神经元。然后，测试时，虽然会传递所有的神经元信号，但是对于各个神经元的输出，要乘上训练时的删除比例后再输出。

        通过使用Dropout，训练数据和测试数据的识别精度的差距变小了，并且训练数据也没有达到100%的识别精度。像这样，通过使用Dropout，即使是表现力强的网络，也可以抑制过拟合，即实际使用时效果较好。

 第七章 卷积神经网络

        Convolutional Neural Network,CNN，常用于图像识别和语音识别。 主要包含输入层、卷积层、激活函数（输出层常使用Softmax，其他层常使用ReLu）、池化层、Dropout层、BN层、全连接层(通常使用Affine)、输出层。

卷积层

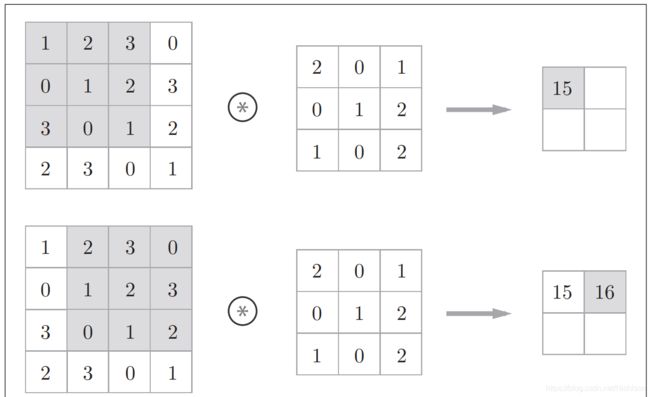
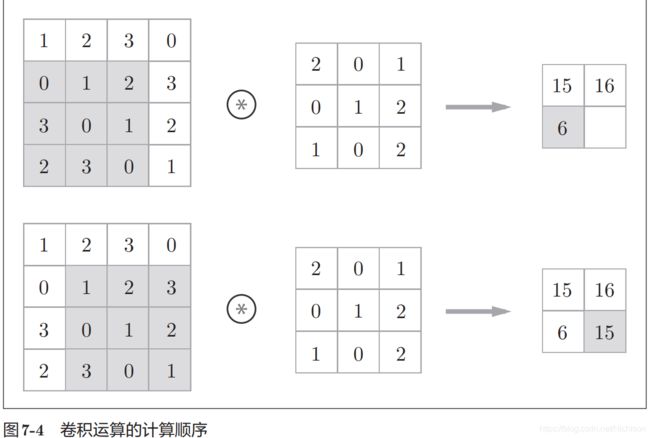
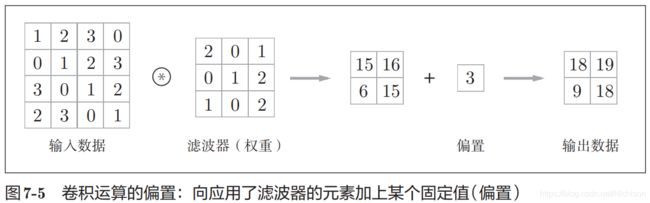
        分析数学中的一种运算，本质是用卷积核的参数来提取数据的特征，通过矩阵点乘运算与求和运算来的到结果。

         如果每次进行卷积运算都会缩小空间，那么在某个时刻输出大小就有可能变成1，导致无法再应用卷积运算，为了避免出现这种情况，所以要使用填充。

        并且卷积运算的步幅可以大于1，增大步幅，输出尺寸会变小，而填充后，输出尺寸会变大。通过以下公式可以计算输出尺寸大小。

        设输入尺寸为（H,W），滤波器尺寸为（FH,FW），输出尺寸为（OH,OW），填充为P，步幅为S。此时输出尺寸为

         注意：必须使分式可以除尽；当P=S=FH=FW时，输入输出的长宽不变，也就是说在H*W*C的特征图上进行步幅和填充为1的1*1*C卷积时，可以将输出变成H*W*1，即1*1卷积可以实现降维操作，且不改变图片尺寸，当有多个1*1卷积时，还可以实现升维。

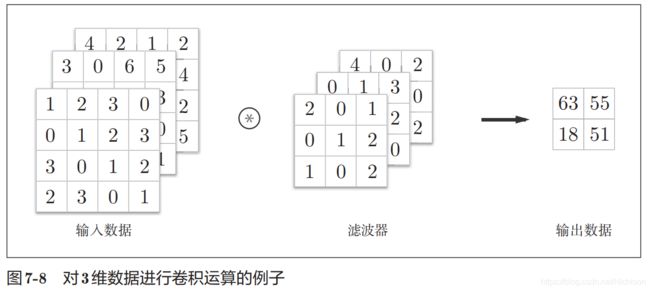
 通道方向上有多个特征图

         会按通道进行输入数据和滤波器的卷积运算，并将结果相加，从而得到输出。

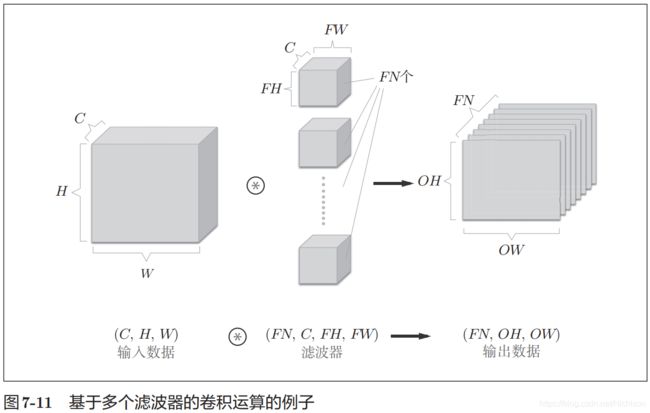
通道方向上有多个滤波器

        这样输出也可以有多个输出。

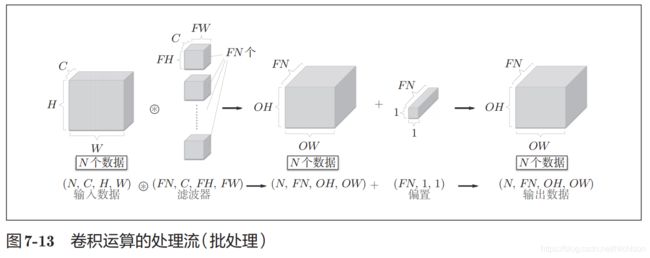
        同时可以应用批处理，一次有多个输入。

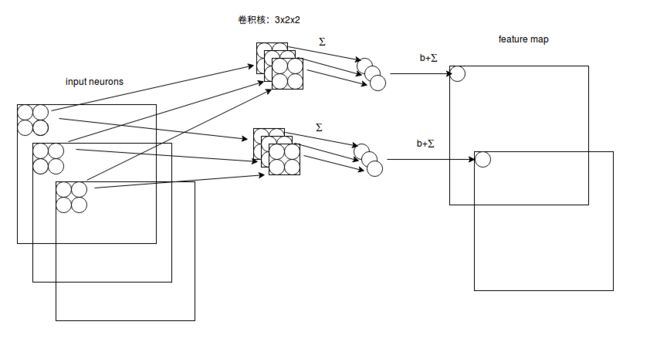
        多通道多滤波器卷积计算方式示意如下：

          完整的网络维度如下图。

激活函数层

        为了从卷积运算的结果提取出高语义信息，需要用到激活函数，一般为非线性的映射，常用的包括Sigmoid、ReLU及Softmax函数。

Sigmoid

        模仿了生物的神经元特性，当神经元获得的输入信号累计超过一定的阈值后，神经元被激活，否则处于抑制状态。

 

ReLU（Rectified Linear Unit，修正线性单元）

        为了缓解梯度消失的现象，引入ReLU，由于其优越的性能与简单优雅的实现，已经成为目前卷积神经网络中最为常用的激活函数之一。

Softmax

        针对多目标分类问题而设计，主要用在全连接层最后一层。

        在具体的分类任务中，其输入往往是多个类别的得分，输出则是每一个类别对应的概率，概率值在0-1之间，总和为1。

>>> import torch.nn.functional as F
>>> score = torch.randn(1,4)
>>> score
tensor([1.3858, -0.4449, -1.7636, 0.9768])
>>> F.softmax(score, 1)
tensor([0.5355, 0.0858, 0.0230, 0.3557])

池化层

        用于缩小高、长方向上的空间运算，降低特征图的参数量，提升计算速度，增加感受野，并能在一定程度上防止过拟合。

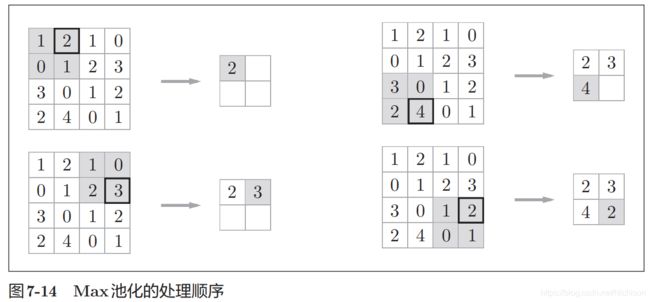
        池化有多种方式，max池化是获取最大值的池化方式，另外还有average池化等。

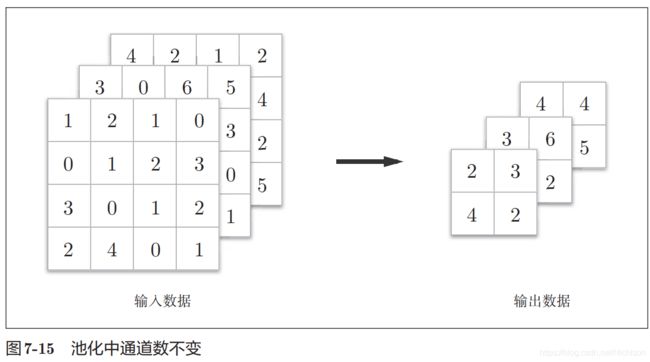
         池化不会改变输入数据和输出数据的通道数。

         池化对输入数据的微小偏差有鲁棒性。

Dropout层

        为了缓解过拟合而出现的，在训练时，每个神经元以概率p保留，即以1-p的概率停止工作，每次前向传播保留下来的神经元都不同，这样可以使得模型不太依赖于某些局部特征。

BN层

        随着网络深度越来越深、参数越来越多，网络也变得越发难以收敛和调参，原因在于浅层参数的微弱变化经过多层变换后会被放大。

        BN层首先对每一个batch的输入特征进行白化操作，即去均值方差过程。

        假设一个batch的输入数据为，首先计算其均值和方差和，然后执行下式。

        白化操作可以使输入的特征分布具有相同的均值与方差，固定了每一层的输入分布，从而加速网络的收敛。然而他也限制了网络中数据的表达能力，浅层学到的参数信息会被白化操作屏蔽掉，为此BN层在白化操作后又增加了一个线性变换操作，让数据尽可能地恢复本身的表达能力。

        和为新引入的可学习参数。

        BN层的优点包括缓解梯度消失，加速网络收敛；简化调参，网络更稳定；防止过拟合；

        BN层的缺点包括需要较大的batch才能发挥作用；数据的batch在训练与测试时往往不一样，这样导致测试集依赖于训练集，然而有时候训练集与测试集的数据分布不一致。

全连接层

        一般连接到卷积网络输出的特征图后，特征时每一个节点都与上下层的所有节点相连，所以参数量上是最多的。

第八章 深度学习