决策树续-连续值处理与剪枝策略

连续值处理

连续值离散化

 连续值的选取不再是简单的有限的1，2，3等等，无法用暴力枚举的方式计算。因此第一步就是要把连续值进行离散化，常用的离散化策略是二分法

 

– 第一步：将连续属性 a 在样本集 D 上出现 n 个不同的取值从小到大排列，记为 a 1 , a 2 , ..., an。基于划分点t，可将D分为子集Dt +和Dt-，其中Dt-包含那些在属性a上取值不大于t的样本，Dt+包含那些在属性 a上取值大于t的样本。考虑包含n-1个元素的候选划分点集合即把区间[a i , a i-1) 的中位点 (a i+a i-1)/2作为候选划分点

– 第二步：采用离散属性值方法，计算这些划分点的增益，选取最优的划分点进行样本集合的划分：其中Gain(D, a, t)是样本集D基于划分点 t 二分后的信息增益，于是， 就可选择使Gain(D, a, t)最大化的划分点.

以西瓜书为例

图一

以密度为例：

density=[0.697,0.774,0.634,0.608,0.556,0.403,0.481,0.437,0.666,0.243,0.245,0.343,0.639,0.657,0.360,0.593,0.719];

 步骤1：将连续值从小到大排列

 0.2430    0.2450    0.3430    0.3600    0.4030    0.4370    0.4810    0.5560    0.5930    0.6080    0.6340    0.6390    0.6570    0.6660    0.6970    0.7190    0.7740

取相邻两个数的平均值，17个数据将会有16个结果

候选值：0.2440 0.2940 0.3515 0.3815 0.4200 0.4590 0.5185 0.5745 0.5855 0.6210 0.6365 0.6480 0.6615 0.7080 0.7465 

 步骤2：计算各候选值的增益

当t=0.2440时，={0.2430}，={0.2450,0.3430,0.3600.......0.7190,0.7740}

当t=0.2940时，={0.2430，0.2450}，={0.3430,0.3600.......0.7190,0.7740}

同理计算出所有候选值的增益。最终结果为当t=0.3815时，Gain（D，a，t）=0.263为最大值，故选0.3815为划分点。

剪枝策略 

预剪枝

预剪枝通常有三种策略：

1.直接定义决策树的高度h，当决策树的高度超出h时停止生长

2.定义节点的样本数量阈值，当样本数量小于阈值是停止生长

3.计算决策树生长后是否对决策结果有提升，当没有提示或是小于一个规定的阈值时停止生长 

如下一颗为剪枝的决策树（图二），以图一为数据集（删去密度和含糖量）

 

图二

 

采用第一种方法定义高度为4时，则纹理分类将不会展开，并且根据样本的正例返例数量生成叶子节点，也就是好瓜。

采用第二种方法：定义样例数量阈值为5，则脐部稍凹，根蒂稍蜷，色泽乌黑将不再生成子树（样例为4）

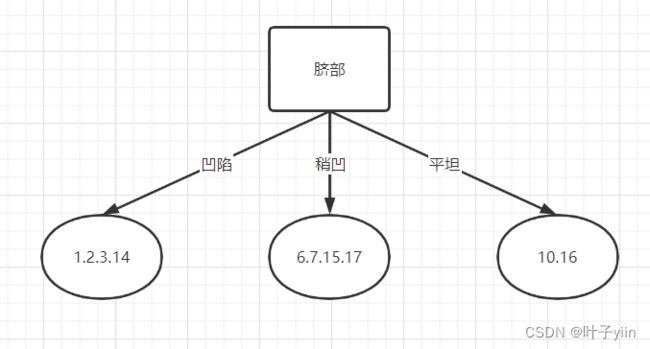
采用第三种方法：若用1.2.3.6.7.10.14.15.16.17来做训练集，剩下的做测试集，用脐部做根节点（图三），此时所有样例都在根节点（好瓜），测试集测试得准确率为43.9%。划分后凹陷为好瓜，稍凹为好瓜，平坦为坏瓜。则此时准确率为 71.4%。相比未划分时有提升，则应该往下生长。

图三

 由于预剪枝一定程度采用了贪心算法，所以可能会出现当前节点划分不能够提升准确率，但划分之后再划分是提升准确率的情况。也就是把更好的分支提前扼杀了，会导致欠拟合现象。

后剪枝

后剪枝就是在一颗完整的决策树上从下往上的搜素，判断将当前节点换成叶节点后是否对总体性能有所提升。若将该结点对应的子树换为叶结点能够带来泛华性能的提升，则把该子树替换为叶结点。

同样用图二进行举例。将纹理节点替换为叶节点。节点样本有7.15，正反例相同，取正例。剪枝完结果如图四，剪枝后准确率为57.1%，有所提升，所以将其剪枝。

图四

 附上实现：

import operator
from collections import Counter
from math import log

import numpy as np

import treePlotter


def get_data():
    # 特征矩阵
    feat_matrix = np.array([
        ['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.697, 0.460],
        ['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', 0.774, 0.376],
        ['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.634, 0.264],
        ['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', 0.608, 0.318],
        ['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.556, 0.215],
        ['青绿', '稍蜷', '浊响', '清晰', '稍凹', '软粘', 0.403, 0.237],
        ['乌黑', '稍蜷', '浊响', '稍糊', '稍凹', '软粘', 0.481, 0.149],
        ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '硬滑', 0.437, 0.211],
        ['乌黑', '稍蜷', '沉闷', '稍糊', '稍凹', '硬滑', 0.666, 0.091],
        ['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘', 0.243, 0.267],
        ['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑', 0.245, 0.057],
        ['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘', 0.343, 0.099],
        ['青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑', 0.639, 0.161],
        ['浅白', '稍蜷', '沉闷', '稍糊', '凹陷', '硬滑', 0.657, 0.198],
        ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘', 0.360, 0.370],
        ['浅白', '蜷缩', '浊响', '模糊', '平坦', '硬滑', 0.593, 0.042],
        ['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑', 0.719, 0.103]
                                                                                ])


    values_size = feat_matrix.shape[0]
    for discretefeat_idx in range(6):  # 6个离散特征
        dict_value_encode = {}
        encode = 0
        for value in feat_matrix[:,discretefeat_idx]:
            if value not in dict_value_encode.keys():
                encode += 1
                dict_value_encode[value] = encode
        for value_idx in range(values_size):
            feat_matrix[value_idx][discretefeat_idx] = dict_value_encode[feat_matrix[value_idx][discretefeat_idx]]
    feat_matrix = feat_matrix.astype(np.float64)
    # 类别标签
    labels = np.array(['是', '是', '是', '是', '是', '是', '是', '是',
                       '否', '否', '否', '否', '否', '否', '否', '否', '否'])
    # 特征名
    feat_names = np.array(['Colour', 'roots', 'knock', 'texture', 'Belly button', 'touch','density','sugar content'])
    return feat_matrix,labels,feat_names

# 计算经验熵
def cal_entropy(x):
    x_set = set(x)
    x_size = x.shape[0]
    entropy = 0.0
    for label in x_set:
        p = np.count_nonzero(x == label) / x_size
        entropy -= p * log(p,2)
    return entropy

# 根据选定特征计算条件信息熵
def cal_conditionalentropy(feat_values,labels):
    values_set = set(feat_values)
    values_size = feat_values.shape[0]
    c_entropy = 0.0
    for value in values_set:
        p = np.count_nonzero(feat_values == value)/values_size
        c_entropy += p * cal_entropy(labels[feat_values == value])
    return c_entropy

def cal_min_conditionalentropy(feat_values,labels):
    values_size = feat_values.shape[0]
    zip_feat_values_labels = dict(zip(feat_values,labels)) # 将连续特征取值和对应的分类标签zip起来
    # 按照特征值升序排序,分类标签跟着一起排
    zip_feat_values_labels_sorted = dict(sorted(zip_feat_values_labels.items(),key=operator.itemgetter(0)))
    feat_values_sorted = np.array(list(zip_feat_values_labels_sorted.keys())) # 排序过后的特征取值
    labels_sorted = np.array(list(zip_feat_values_labels_sorted.values()))  # 排序过后的分类标签
    thresholds = [(feat_values_sorted[idx]+feat_values_sorted[idx+1])/2  # n个特征取值有n-1个缝隙,得n-1个阈值
                  for idx in range(feat_values_sorted.shape[0]-1)]
    min_c_entropy = float('inf')
    min_c_entropy_threshold = (feat_values_sorted[0] + feat_values_sorted[1])/2 # 初始化阈值是第一个缝隙中的
    for threshold in thresholds:
        filter_left = feat_values_sorted <= threshold  # 阈值左边的部分
        feat_values_left = feat_values_sorted[filter_left]
        labels_left = labels_sorted[filter_left]

        filter_right = feat_values_sorted > threshold  # 阈值右边的部分
        feat_values_right = feat_values_sorted[filter_right]
        labels_right = labels_sorted[filter_right]
        c_entropy = feat_values_left.shape[0]/values_size*cal_entropy(labels_left) +\
                    feat_values_right.shape[0]/values_size*cal_entropy(labels_right)
        if c_entropy <= min_c_entropy:
            min_c_entropy = c_entropy
            min_c_entropy_threshold = threshold
    return min_c_entropy,min_c_entropy_threshold  # 返回有二,最小的条件信息熵和对应的阈值

# 根据选定特征计算信息增益
def cal_info_gain(feat_values,labels):
    # 如果是离散值
    if feat_values[0].item()>=1:
        return cal_entropy(labels) - cal_conditionalentropy(feat_values,labels),'discrete'
    # 如果是连续的
    else:
        min_c_entropy, min_c_entropy_threshold = cal_min_conditionalentropy(feat_values,labels)
        return cal_entropy(labels) - min_c_entropy,min_c_entropy_threshold


# 根据选定特征计算信息增益比
def cal_info_gain_ratio(feat_values,labels):
    return (cal_info_gain(feat_values,labels) + 0.01)/(cal_entropy(feat_values)+0.01)


# 生成决策树中的第二个终止条件满足时,返回实例数最大的类
def get_max_label(labels):
    return Counter(labels)[0][0]

# 选择信息增益、信息增益比最大的特征
def get_best_feat(feat_matrix,labels):
    feat_num = feat_matrix.shape[1]
    best_feat_idx = -1
    max_info_gain = 0.0
    ret_sign = 'discrete'  # 默认是离散的
    for feat_idx in range(feat_num):
        feat_values = feat_matrix[:,feat_idx]
        info_gain,sign = cal_info_gain(feat_values,labels)
        if info_gain >= max_info_gain:
            max_info_gain = info_gain
            best_feat_idx = feat_idx
            ret_sign = sign
    return best_feat_idx,ret_sign

# 根据选定特征,划分得到子集
def get_subset(feat_matrix,labels,best_feat,sign):
    feat_values = feat_matrix[:,best_feat]
    if sign == 'discrete':
        values_set = set(feat_values)
        feat_matrix = np.delete(feat_matrix,best_feat,1)
        feat_matrixset = {}
        labelsset = {}
        for value in values_set:
            feat_matrixset[value] = feat_matrix[feat_values==value]
            labelsset[value] = labels[feat_values==value]
    # 连续值
    else:
        threshold = sign
        feat_matrixset = {}
        labelsset = {}
        # 左
        filter_left = feat_values <= threshold
        feat_matrixset['<={}'.format(threshold)] = feat_matrix[filter_left]
        labelsset['<={}'.format(threshold)] = labels[filter_left]
        # 右
        filter_right = feat_values > threshold
        feat_matrixset['>{}'.format(threshold)] = feat_matrix[filter_right]
        labelsset['>{}'.format(threshold)] = labels[filter_right]
    return feat_matrixset,labelsset

def create_decision_tree(feat_matrix,labels,feat_names,method):
    # 首先考虑两种终止条件:1、类别标签只有一种类型 2、特征没有其他取值
    if len(set(labels)) == 1:
        return labels[0] # 类型为numpy.int32
    if feat_matrix.shape[0] == 0:
        return get_max_label(labels)
    # 选择信息增益最大的特征，sign标志着是离散特征还是连续特征，若连续，sign为阈值
    best_feat,sign = get_best_feat(feat_matrix,labels)
    best_feat_name = feat_names[best_feat]
    # 初始化树
    decision_tree = {best_feat_name:{}}
    # 如果是离散的,则要删除该特征，否则不删。思考:连续特征何时删？当
    if sign == 'discrete':
        feat_names = np.delete(feat_names,best_feat)
    # 得到子集(得到字典类型的子集,键为选定特征的不同取值)
    feat_matrixset, labelsset = get_subset(feat_matrix,labels,best_feat,sign)
    # 递归构造子树
    for value in feat_matrixset.keys():
        decision_tree[best_feat_name][value] = create_decision_tree(feat_matrixset[value],labelsset[value],feat_names,method)
    return decision_tree
if __name__ == "__main__":
   feat_matrix,labels,feat_names = get_data()
   decision_tree = create_decision_tree(feat_matrix,labels,feat_names,method='ID3')
   print(decision_tree)
   treePlotter.createPlot(decision_tree)