理解梯度下降法

学习笔记更新
什么是梯度下降法？一个基于搜索的最优化方法，每一步都沿着当前梯度的方向，最后到达目标。在训练神经网络时，求解损失函数的最小值。当然，把它理解为寻找函数最小值的方法也是对的，个人认为，这句话虽然没毛病，但更偏向于梯度下降法的应用。

引入

直观解释梯度下降法，最常出现的例子就是在不考虑安全因素的情况下，求解一个人怎样尽快从山顶到山脚。（不不可以飞，只能走！） 这里我们不考虑步行速度，所以问题转换为从山顶找一条到达山底的最短路径。为了找到这条路径，我们首先要确定方向，在360°的周围，朝哪个方向迈一步可以使垂直距离下降最大？其次，因为山的坡度不是从山顶到山底一成不变的，迈出一步后需要在所站位置上继续选择方向，这里就引出了第二个因素：步长。一步迈的太大，容易错过最佳路径。步长太小，走一小步，判断一下，走一小步，判断一下…….，迭代次数会增加，时间开销变大。因此，最优的方向和合适的步长才是求解问题的关键。
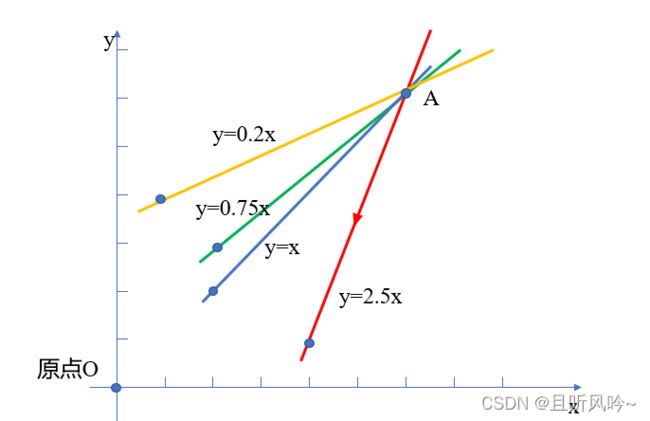
在下列二维直角坐标系中，假设步长为0.5，从点A出发，如何尽快从A点到达原点O呢？显然，当前位置，红色路径是最好的选择。为什么呢？因为红色直线上箭头所指的方向是梯度的方向。

一、 梯度

  "梯度的本质是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。"---- 摘自百度百科

梯度是一个矢量，有方向有大小。在上述二维直角坐标系中，在步长相等的前提下，A点梯度的方向就是垂直距离下降最快的方向，即红色箭头所指的方向。梯度的大小，为红色直线对应方程的导数值。
在三维直角坐标系中，如下图，

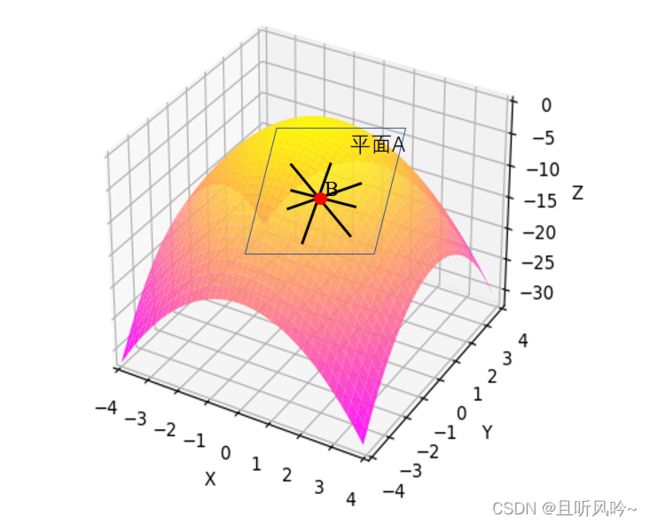
怎么计算点B的梯度呢。在二维图中，求函数导数，对x求导即可。三维图的曲面是二元函数，z=F（x,y) , B点梯度的方向为Z值变化最快的方向，Z值的变化，由x,y共同决定，因此，引入偏导数。

    “在数学中，一个多变量的函数的偏导数，就是它关于其中一个变量的导数而保持其他变量恒定（相对于全导数，在其中所有变量都允许变化）”           ---摘自百度百科

分别对x,y进行求导，求一个变量求导时，把另外一个变量当作常数。

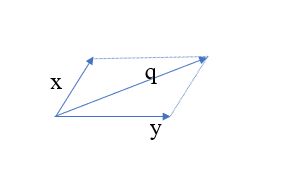
求出来的偏导数是z值沿着x方向或y方向变化最快。可以看到，在三维图中，不只是有x,y两个方向，四面八方都有可以走的路。因此，引入方向导数。“方向导数是在函数定义域的内点对某一方向求导得到的导数”。z值的变化受x，y影响，需要找出最大的方向导数，最大的方向导数对应的直线所在方向就是梯度的方向。如三维图中，点B所有的切线都在同一切平面上，问题可以归结为二维图中的情况，必然存在一个绝对值最大的方向导数，方向导数对应的那条切线就是梯度所在的方向（上升/下降）。方向导数是各个偏导数与对应夹角余弦值的组合。如下图，平行四边形法则中，q向量是x向量与y向量共同作用后产生的和向量，在众多方向导数中，q方向的导数绝对值最大，因此q方向即为梯度的方向。

二、什么是梯度下降法

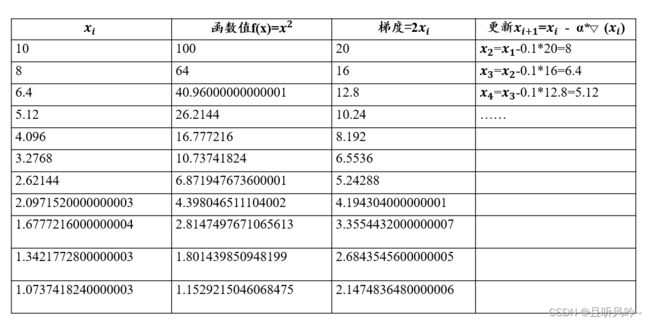
在清楚什么是梯度之后，梯度下降法就很好理解了。站在山顶的人，沿着梯度的方向，走一步，然后继续沿着该点梯度的方向继续走，直至走到山脚。（梯度的方向是垂直距离下降最大的方向）。怎么计算当前位置的梯度呢？整个梯度下降法的过程是怎样的呢？以一元二次方程为例，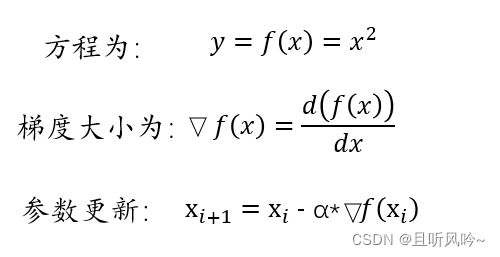
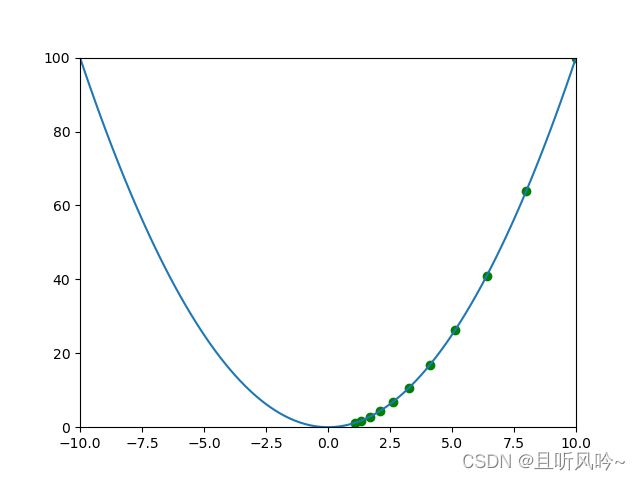
假设x初始为10，y 则为100，从点（10，100）处开始，通过搜索，一步步找到函数的最小值。步长设置为0.1
编写程序，可视化 下降过程：

迭代过程，变量更新：

三、线性回归问题中的梯度下降法

在线性回归问题中，以二元线性回归为例：现有一些样本，每个样本具有X1，X2特征。需要拟合出一个平面，使得这个平面能对样本进行清晰的划分。如何得到平面呢？设平面方程为Z，Z=w1x1+w2x2, 对于每个样本来说，x1，x2值是已知的，因此，w1,w2取值影响模型输出结果。我们可以把其想象成z是关于w1,w2的函数。在下面这个散点图中，横轴是X1值，纵轴为X2值。

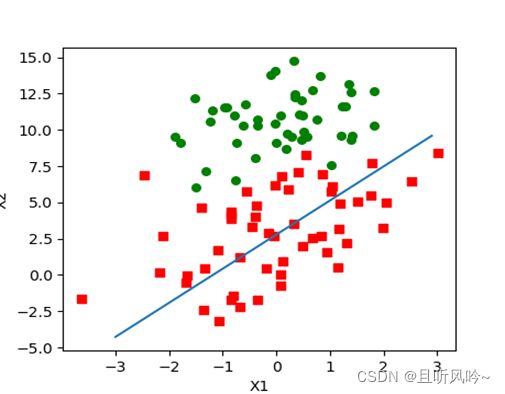
假设在上面的散点图中，z=40是两种类别的分界线，z>40是第一类，z<40是第二类。那么我们需要调节w1,w2值，当输入X1，X2时，使得结果尽量是真实标签所在的范围。通俗一点说，现有样本1，X1, X2已知，类别是属于第二类，z值为32, 我们计算出来，z值为47，为了使其划分正确，我们要使z值靠近40甚至低于40,与真实值32更加贴近。通过梯度下降法，对w1、w2进行更新，寻找函数的最小值，使得计算出来的值与它的真实值尽可能的相近。尽量使所求平面能对所有样本点进行正确划分。多个样本时，最小化损失函数J

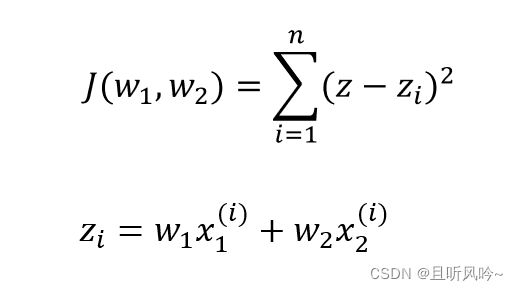
通过梯度下降法，求解损失函数最小值，损失函数越小，得到的平面能对越多的点进行正确分类。
例如，x1=2，x2=3时，那么z=2w1+3w2，这就是二元方程，换成经常看到的形式，z=2x+3y,做出平面，通过调节x（w1）,y (w2) 值，使得z能满足不同样本的要求，当Z能满足许多样本的需求时，损失函数值就会越小，x（w1）,y (w2) 值最终确定后，平面方程也就求出了。

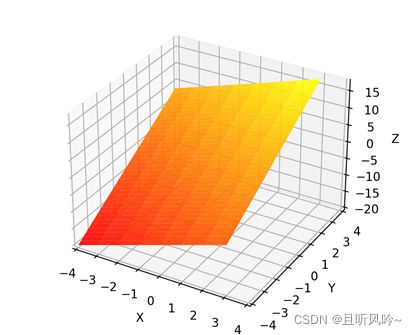
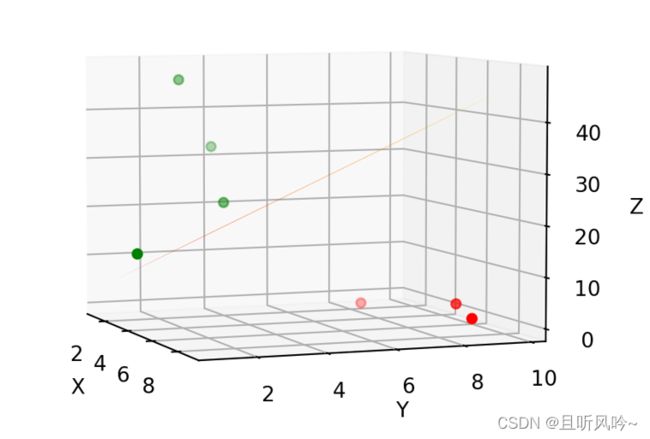
线性回归问题，数据是线性可分的，通过对所有样本进行拟合，最后找到一个平面，可以对数据点进行良好的分类。如果数据是严格线性可分的，那么我们就可以对所有的数据进行正确分类。如，假设有8个数据点在三维空间的分布情况如图：


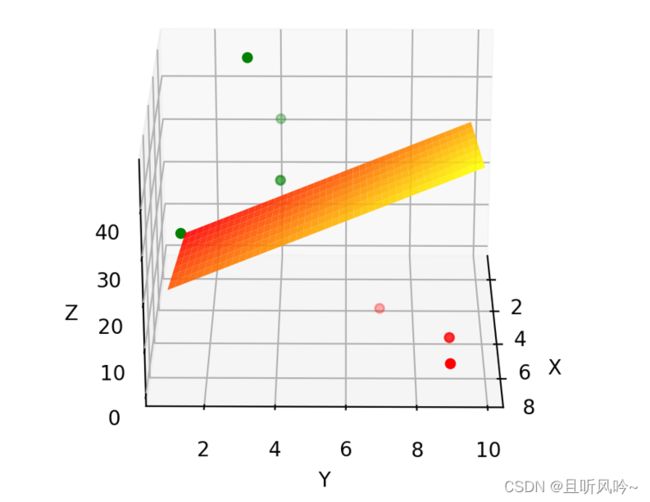
图中的线性平面2x+3y刚好可以对数据点进行完美划分,w1=2,w2=3。线性平面的参数(w1,w2)就是通过梯度下降法更新的，这就是梯度下降在二元线性回归问题中的应用。

四、总结：

1、梯度下降法是一个基于搜索的最优化方法，常用于求目标函数最小值，与之对应，梯度上升法，求目标函数最大值。当目标函数是凸函数时，所求解为全局最优解。但一般情况下，目标函数基本不是凸函数，很有可能得到的解是局部最优，得到全局最优解是概率事件。
2、根据参与参数更新的样本选择方式以及数量上的不同，梯度下降法又分为批量梯度下降BGD（整个样本集遍历一遍，参数更新一次）、随机梯度下降SGD（随机挑选样本进行参数更新），小批量梯度下降MBGD（选择一部分样本，进行参数更新）。

学海无涯，个人整理，内容难免会有纰漏，欢迎道友指正，感激不尽！