机器学习实战——Kmeans聚类算法

1 聚类算法介绍

在无监督学习中，训练样本的标记是未知的，目标是通过对无标记训练样本的学习来揭示数据的内在性质及规律，为进一步的数据分析提供基础。聚类分析是无监督学习中的典型代表，其中比较常见的聚类算法有：K-均值聚类、密度聚类与层次聚类。接下来的文章逐一对三种聚类算法进行介绍。

1.1 K-均值聚类

K-均值聚类的基本思想是，对于给定的样本集，随机选择 k 个点作为初始点，按照样本间的距离大小，将样本集划分为 k 个簇，且簇内的点均方误差尽量小，簇间的点均方误差尽量大。假设给定样本集为 $D=\{x_1,x_2,...,x_m\}$,划分的簇 $C=\{C_1,C_2,...,C_k\}$,则其划分簇的平方误差数学表达式如下：

$$E=\sum _{i=1}^k\sum _{x\in C_i}{\mid \mid x-{\mu }_i\mid \mid }_2^2$$

其中 ${\mu }_i$ 是簇 $C$ 的均值向量，也成为质心，表达式为：

$${\mu }_i=\frac{1}{\mid C_i\mid }\sum _{x\in C_i}x$$

其算法流程如下：

在上述算法流程中，由于 k 值是随机选取的，对聚类的效果有较大的影响。kmeans++ 算法减弱了初始点随机性的影响。kmeans++ 算法的基本思想是：初始的聚类中心之间的相互距离要尽可能的远。其算法描述有如下两种：
描述1（可以参考这篇文章）：

1 从输入的数据点集合中随机选择一个点作为第一个聚类中心。
2 对于数据集中的每一个样本点 $x$，计算它与最近聚类中心(指已选择的聚类中心中距离最短的)的距离 $D(x)$
3 选择一个新的数据点作为新的聚类中心，选择的原则是：$D(x)$ 较大的点，被选取作为聚类中心的概率较大
4 重复 2 和 3 直到 k 个聚类中心被选出来

其第 3 步的具体步骤如下：

1.先从我们的数据库随机挑个随机点当“种子点”
2.对于每个点，我们都计算其和最近的一个“种子点”的距离 $D(x)$ 并保存在一个数组里，然后把这些距离加起来得到 $Sum(D(x))$。
3.然后，再取一个随机值，用权重的方式来取计算下一个“种子点”。这个算法的实现是，先取一个能落在 $Sum(D(x))$ 中的随机值 Random （Random=Sum(D(x))*（0-1之间的一个随机数）），然后用 Random -= D(x)，直到其 <= 0，此时的点就是下一个“种子点”。
4.重复 2 和 3 直到k个聚类中心被选出来

描述2（可以参考这篇文章）：

1 从数据集中随机选取一个样本点作为初始聚类中心;
2 首先计算每个样本与当前已有聚类中心之间的距离（即最短距离：当选择第 n+1 个聚类中心时，选择各样本点与前 n 个聚类中心的最短距离），用 $D(x)$ 表示；接着计算每个样本点被选为下一个聚类中心的概率 $\frac{D(x{)}^2}{{\sum }_{i=1}^{n}D(x_i{)}^2}$，最后，按照轮盘法（即利用 0-1 的随机数，按照选择的概率值落的区间选择聚类中心点）选择出下一个聚类中心；
3 重复第 2 步直到选择出 k 个聚类中心；

描述 2 中的 $D(x)$ 与 $Sum(D(x))$ 与描述 1 中的计算方法相同。对于 kmeans 聚类的个数 K 可以使用组内平方误差和来确定最佳聚类数目。

1.2 聚类效果的评价

对于已知样本所属的类别，衡量样本聚类效果的指标有调整的兰德指数（ARI）、互信息等，比较常用的是ARI，ARI 的取值范围为 $[-1,1]$，其值越大，聚类效果越好。如果不知道样本的真实类别，则必须使用模型本身进行度量，即从簇内的稠密程度和簇间的离散程度来评估聚类的效果，比较常用的指标有 Silhouette Coefficient、Calinski-Harabasz Index，其值越大聚类效果越好。上述评价指标在 sklearn 的 metrics 类均有对应的方法可以调用。详细的情况可以参考官网的 聚类效果评价部分。

2 sklearn中的实现

class sklearn.cluster.KMeans(n_clusters=8, init=’k-means++’, n_init=10, max_iter=300, tol=0.0001, precompute_distances=’auto’, verbose=0, random_state=None, copy_x=True, n_jobs=None, algorithm=’auto’)

主要参数说明：

• n_clusters：设定的聚类个数。
• max_iter：最大的迭代次数，一般如果是凸数据集的话可以不管这个值，如果数据集不是凸的，可能很难收敛，此时可以指定最大的迭代次数让算法可以及时退出循环。
• n_init：用不同的初始化质心运行算法的次数。由于 K-Means 是结果受初始值影响的局部最优迭代算法，因此需要多跑几次以选择一个较好的聚类效果，一般选择默认值10。若 k 值较大，则可以适当增大该值。
• init： 初始样本点选择的方式，可以为完全随机选择 ‘random’ ,优化过的 ‘k-means++’ 或者自己指定初始化的 k 个质心。默认的是 ‘k-means++’ 。
• precompute_distances：布尔值，预计算距离，计算速度更快但占用更多内存，默认为 auto 。
• algorithm：有 auto、full、elkan 三种选择。full 就是传统的 K-Means 算法， elkan 是 elkan K-Means 算法。默认的 auto 则会根据数据值是否是稀疏的，来决定如何选择 full 和 elkan。一般数据是稠密的 elkan，否则就是 full 。一般来说建议直接用默认的 auto。

# kmeans聚类的效果评价函数
sklearn.metrics.calinski_harabaz_score(X, labels)
# X：样本特征 labels：预测的聚类类别 上述结果值越大，聚类效果越好。
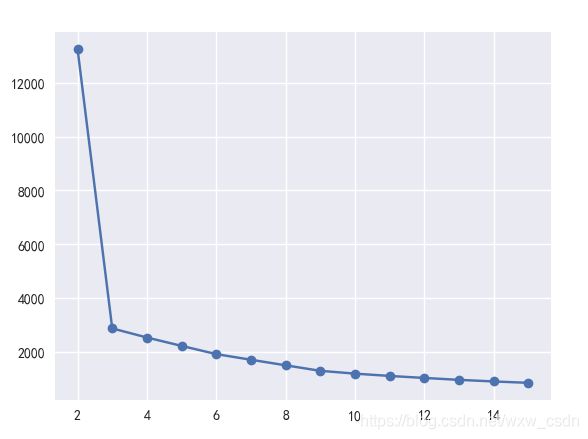
# 也可以使用组内平方和与分组个数的图形确定聚类的类别。

# make_blobs有3个聚类簇
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei'] #中文显示问题
plt.rcParams['axes.unicode_minus'] = False #负数显示问题

n_samples = 1500
random_state = 170
X,y = make_blobs(n_samples=n_samples, random_state=random_state)
 
sum_err = [] #记录不同聚类个数的组内平方和
for i in range(2,16):
    test = KMeans(n_clusters=i,random_state=random_state).fit(X)
    sum_err.append(test.inertia_)
# 画出组内平方和与类别的图形，有图知分为三个类别较合适    
plt.plot(range(2,16),sum_err,'o-')
 
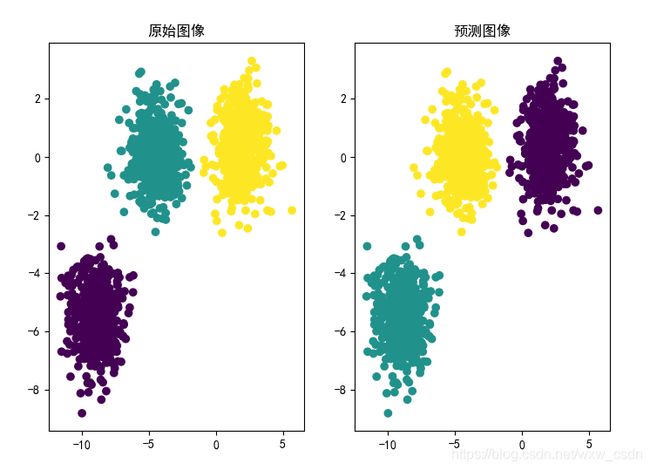
plt.subplot(1,2,1)
plt.scatter(X[:,0],X[:,1],c=y)
plt.title('原始图像')
# 定义聚类对象 
clf = KMeans(n_clusters=3,random_state=random_state)
# 调用对象
clf.fit(X)
#调用该对象进行预测
y_predict = clf.predict(X) 
# 上述聚类过程可以一次完成
# y_predict = KMeans(n_clusters=3, random_state=random_state).fit_predict(X)
plt.subplot(1,2,2)
plt.scatter(X[:,0],X[:,1],c=y_predict)
plt.title('预测图像')