PCA实现降维
0. 前言
上篇博客通过举例说明了降维如何实现,下面将学习PCA这种降维算法。
1. PCA介绍
PCA(Principal Component Analysis),主成分分析,即找出一个最主要的特征,进行分析。
PCA使用方差作为信息量的衡量指标,使用特征值分解来找空间,降维时,它会通过一些数学方法将特征矩阵X分解成三个矩阵: Q ∑ Q − 1 Q\sum Q^{-1} Q∑Q−1; Q Q Q和 Q − 1 Q^{-1} Q−1是辅助矩阵, ∑ \sum ∑是对角矩阵(对角线有值,其余为0),故对角线上就是方差。降维后,PCA寻得的每个新的特征向量就是“主成分”,而那些被删掉的特征向量就是信息量很少的。
关于降维过程的实现,可以看见上篇博客
2. 调用sklearn库实现
对于鸢尾花数据集,其特征矩阵是四维的,是肉眼没法观察的,所以希望通过降维再将其可视化,以查看其数据的分布。
- 数据集
此处采用鸢尾花数据集,该数据集有150个样本,每个样本4个特征,有3个类别。
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import pandas as pd
# 加载鸢尾花数据集
iris = load_iris()
X = iris.data
y = iris.target
print("数组维度:", X.shape) # 二维数组
iris_dataFrame = pd.DataFrame(X) # 四维特征矩阵
print("特征矩阵:\n", iris_dataFrame)
输出结果:
数组维度: (150, 4)
特征矩阵:
0 1 2 3
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
.. ... ... ... ...
145 6.7 3.0 5.2 2.3
146 6.3 2.5 5.0 1.9
147 6.5 3.0 5.2 2.0
148 6.2 3.4 5.4 2.3
149 5.9 3.0 5.1 1.8
[150 rows x 4 columns]
根据输出结果可以看出,通过.shape返回2个数字,所以这是一个二维的数组;且对其特征矩阵输出,是一个四维的特征矩阵。
- 调用PCA建模
参数:
n_components:表示降维之后需要的维度,也就是降维后想保留的特征数目。
pca = PCA(n_components=2) # n_components设置降维后的特征数
pca.fit(X) # 拟合
X_new = pca.transform(X) # 获取新矩阵
print("降维后的矩阵:\n", X_new)
print("降维后的维度:", X_new.shape)
输出结果:
降维后的矩阵:
[[-2.68412563 0.31939725]
[ 1.41523588 -0.57491635]
[ 2.56301338 0.2778626 ]
[ 2.41874618 0.3047982 ]
[ 1.94410979 0.1875323 ]
[ 1.52716661 -0.37531698]
[ 1.76434572 0.07885885]
[ 1.90094161 0.11662796]
[ 1.39018886 -0.28266094]]
降维后的维度: (150, 2)
由于数据太多,所以删除了一部分,根据(150, 2)可以看到,成功将4维特征降至2维了。
数据本身是有3类(3种鸢尾花:0,1,2)的,上面的二维特征x1,x2是三种花的特征,如果需要画它们的分布,也就需要从特征矩阵中将这3类分别取出来。可以通过下面这种方式:
# 表示取出标签为0的第一个特征
X_new[y == 0, 0]
# 表示取出标签为0的第二个特征
X_new[y == 0, 1]
- 可视化
# 3. 可视化
plt.figure() # 获取画布
# 画0这类
plt.scatter(X_new[y == 0, 0], X_new[y == 0, 1], c='red', label=iris.target_names[0])
# 画1这类
plt.scatter(X_new[y == 1, 0], X_new[y == 1, 1], c='blue', label=iris.target_names[1])
# 画2这类
plt.scatter(X_new[y == 2, 0], X_new[y == 2, 1], c='green', label=iris.target_names[2])
plt.legend() # 显示图例
plt.show()
- 可视化结果
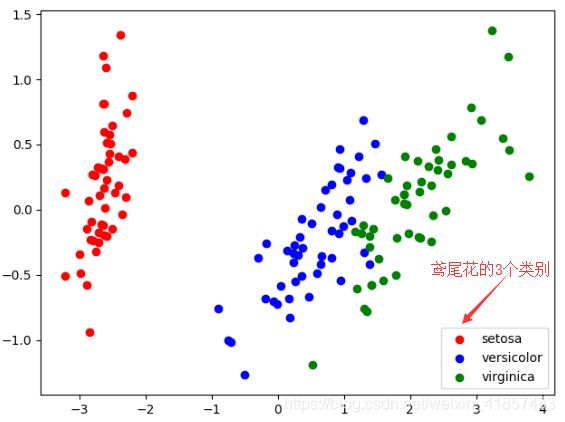
根据上面数据的分布情况,可以看到像分簇分布,且簇间的分布也比较明晰。所以这个数据集用来分类效果一般都会很好。
- 降维后的数据分析
前面通过降维实现了可视化鸢尾花数据集的分布,下面对降维后的数据查看其相关属性。
① explained_variance_:降维后的每个特征向量的方差。
print("方差:", pca.explained_variance_)
"""结果"""
# 方差: [4.22824171 0.24267075]
前面我们将4维特征降至2维,所以是2个方差。可以观察到第一个特征方差很大,其上带有更多的信息量。
② explained_variance_ratio_:可解释性方差贡献率,也就是降维后的新特征信息量占原始数据信息量的比例。
print("可解释性方差贡献率:", pca.explained_variance_ratio_)
"""结果"""
# 可解释性方差贡献率: [0.92461872 0.05306648]
所以大部分有效信息集中在第一个特征上。
对上面两个比例求和,就可以得到在降维之后信息量占原始数据信息量的比例:
print("降维后信息量占原始比例:", pca.explained_variance_ratio_.sum())
"""结果"""
# 降维后信息量占原始比例: 0.9776852063187949
也就是说降维之后信息损失了不到3%.