深度学习机器学习笔试面试题——优化函数

深度学习机器学习笔试面试题——优化函数

提示：重要的深度学习基础知识，大厂们的笔试题，或者面试题都可能考的

说一下你了解的优化函数？
SGD和Adam谁收敛的比较快？谁能达到全局最优解？
说说常见的优化器以及优化思路，写出他们的优化公式
深度学习中的优化算法总结 Optimizer
adam用到二阶矩的原理是什么
Batch的大小如何选择，过大的batch和过小的batch分别有什么影响
梯度下降的思想

---

说一下你了解的优化函数？说说常见的优化器以及优化思路，写出他们的优化公式

一次次地改进！！！
（1）梯度下降法。
梯度下降法是原始的优化方法，梯度下降的核心思想：负梯度方向是使函数值下降最快的方向，因此我们的目标就是求取目标函数的负梯度。
在梯度下降法中，因为每次都遍历了完整的训练集，其能保证结果为全局最优（优点），但是也因为我们需要对于每个参数求偏导，且在对每个参数求偏导的过程中还需要对训练集遍历一次，当训练集很大时，计算费时（缺点）。

（2）批次梯度下降法。
为了解决梯度下降法的**耗时问题 ，批次梯度下降法在计算梯度时，不用遍历整个训练集，而是针对一个批次的数据**。

（3）随机梯度下降法。
再极端一点，就是随机梯度下降法，即每次从训练集中随机抽取一个数据来计算梯度。
因此，其速度较快（优点），但是其每次的优化方向不一定是全局最优的（缺点）。
因为误差，所以每一次迭代的梯度受抽样的影响比较大,也就是说梯度含有比较大的噪声,不能很好的反映真实梯度，并且SGD有较高的方差，其波动较大。而且SGD无法逃离鞍点。

（加粗样式4）Momentum随机梯度下降法
Momentum借用了物理中的动量概念,即前一次的梯度也会参与运算。为了表示动量，引入了 一阶动量 m(momentum)。m是之前的梯度的累加,但是每回合都有 一定的衰减 。
总而言之，momentum 能够加速SGD收敛，抑制震荡。并且动量有机会逃脱局部极小值(鞍点)。

（5）Nesterov动量型随机梯度下降法
Nesterov动量型随机梯度下降法是在momentum更新梯度时加入对当前梯度的校正，让梯度“多走一步”，可能跳出局部最优解。
相比momentum动量法，Nesterov动量型随机梯度下降法对于凸函数在收敛性证明上有更强的理论保证。

（6）Adagrad法
SGD的学习率是线性更新的，每次更新的差值一样。后面的优化法开始围绕自适应学习率进行改进。Adagrad法引入二阶动量，根据训练轮数的不同，对学习率进行了动态调整。
但缺点是Adagrad法仍然需要人为指定一个合适的全局学习率，同时网络训练到一定轮次后，分母上梯度累加过大使得学习率为0而导致训练提前结束。

（7）Adadelta法
Adadelta法是对Adagrad法的扩展，通过引入衰减因子ρ消除Adagrad法对全局学习率的依赖
Adadelta法避免了对全局学习率的依赖。而且只用了部分梯度加和而不是所有，这样避免了梯度累加过大使得学习率为0而导致训练提前结束。

（8）RMSProp法
AdaGrad算法在迭代后期由于学习率过小，可能较难找到一个有用的解。为了解决这一问题，RMSprop算法对Adagrad算法做了一点小小的修改，RMSprop使用指数衰减只保留过去给定窗口大小的梯度，使其能够在找到凸碗状结构后快速收敛。
RMSProp法可以视为Adadelta法的一个特例
RMSProp法缺陷在于依然使用了全局学习率，需要根据实际情况来设定。可以看出分母不再是一味的增加，它会重点考虑距离它较近的梯度（指数衰减的效果）。优点是只用了部分梯度加和而不是所有，这样避免了梯度累加过大使得学习率为0而导致训练提前结束。

（9）Adam法
Adam法本质上是带有动量项的RMSProp法，它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。
Adam法主要的优点在于经过偏置校正后，每一次迭代学习率都有一个确定范围，这样可以使得参数更新比较平稳。

如此9大优化算法，一个个改进来的，最终牛的是Adam优化器，这是大部分训练过程用的优化器。

优化器的公式，流程，优化函数的作用，深度学习中的优化算法总结 Optimizer——最小化损失函数的

下一篇文章，咱会讲损失函数loss，
损失函数是用来度量模型预测值和真实值间的偏差，偏差越小，模型越好，
所以我们需要最小化损失函数。

如何求最小值呢？高中知识告诉我们，对于凸函数可以直接求导可以找到最值，但是神经网络的损失函数往往是非凸函数，我们并不能直接求导。

所以优化函数就可以帮助我们解决这个问题，优化函数就是用来最小化我们的损失函数的。

（1）梯度下降法（gradient descent），
梯度下降（gradient descent）在机器学习中应用十分的广泛，不论是在线性回归还是Logistic回归中，它的主要目的是通过迭代找到目标函数的最小值，或者收敛到最小值。

（2）批次梯度下降法（batch gradient descent）
上面说了，既然遍历整个训练集费时，那么为了提升效率，我们更新参数时只遍历一个批次的数据，即m表示一个批次的数据个数。

（3）随机梯度下降（stochastic gradient descent）
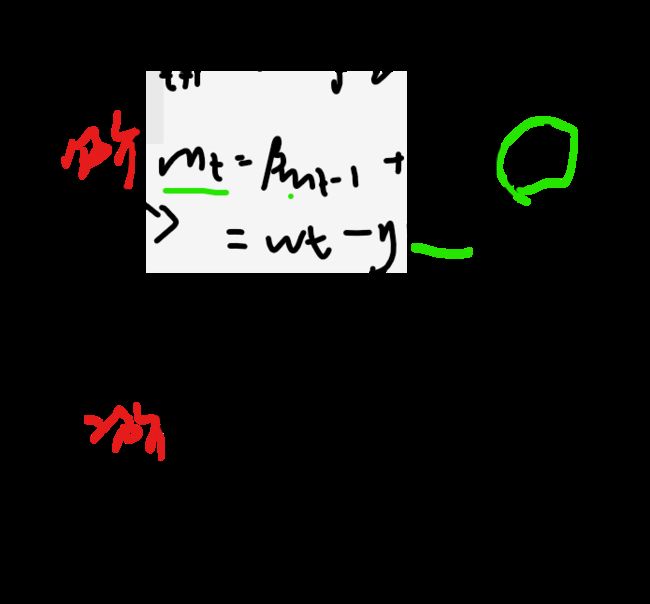
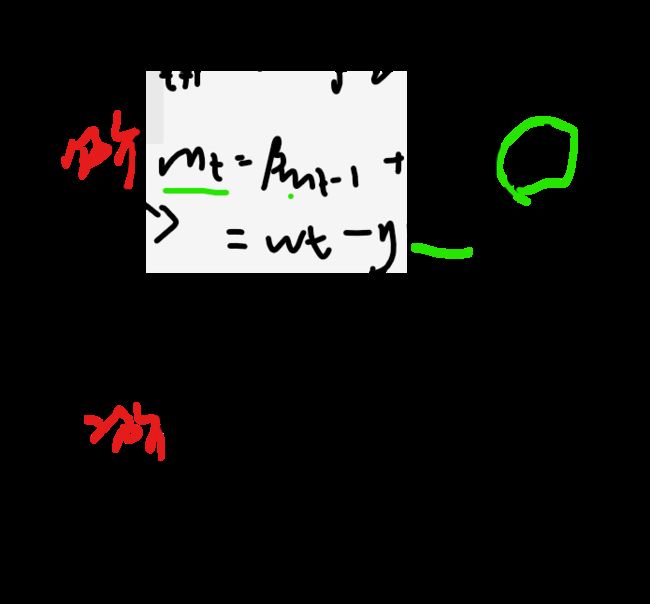
再极端一点，我们一个批次都不要，而是让优化器自己随机选择一个样本，其每次对w的更新，都是针对单个样本数据，并没有遍历完整的参数。当样本数据很大时，可能到迭代完成，也只不过遍历了样本中的一小部分。因此，其速度较快（优点），但是其每次的优化方向不一定是全局最优的（缺点）。因为误差，所以每一次迭代的梯度受抽样的影响比较大,也就是说梯度含有比较大的噪声,不能很好的反映真实梯度，并且SGD有较高的方差，其波动较大。
因为每一次迭代的梯度受抽样的影响比较大，学习率需要逐渐减少，否则模型很难收敛。在实际操作中，一般采用线性衰减：

（4）Momentum随机梯度下降法
核心思想：Momentum借用了物理中的动量概念,即前一次的梯度也会参与运算。为了表示动量，引入了一阶动量m(momentum)。m是之前的梯度的累加,但是每回合都有一定的衰减。公式如下：

（5）Nesterov动量型随机梯度下降法
Nesterov动量型随机梯度下降法是在momentum更新梯度时加入对当前梯度的校正，让梯度“多走一步”，可能跳出局部最优解：

（6）Adagrad法
我们上面讲到了SGD的学习率是线性更新的，每次更新的差值一样。后面的优化法开始围绕自适应学习率进行改进。Adagrad法引入二阶动量，根据训练轮数的不同，对学习率进行了动态调整：

（7）Adadelta法
Adadelta法是对Adagrad法的扩展，通过引入衰减因子ρ消除Adagrad法对全局学习率的依赖，具体可表示为：

（8）RMSProp法
AdaGrad算法在迭代后期由于学习率过小，可能较难找到一个有用的解。为了解决这一问题，RMSprop算法对Adagrad算法做了一点小小的修改，RMSprop使用指数衰减只保留过去给定窗口大小的梯度，使其能够在找到凸碗状结构后快速收敛。RMSProp法可以视为Adadelta法的一个特例，即依然使用全局学习率替换掉Adadelta法中的s_t

（9）Adam法
Adam法本质上是带有动量项的RMSProp法，它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam法主要的优点在于经过偏置校正后，每一次迭代学习率都有一个确定范围，这样可以使得参数更新比较平稳。

优化器的选择，那种优化器最好？该选择哪种优化算法？

目前还没能够达达成共识。
Schaul et al (2014)展示了许多优化算法在大量学习任务上极具价值的比较。虽然结果表明，具有自适应学习率的优化器表现的很鲁棒，不分伯仲，但是没有哪种算法能够脱颖而出。

目前，最流行并且使用很高的优化器（算法）包括SGD、具有动量的SGD、RMSprop、具有动量的RMSProp、AdaDelta和Adam。

在实际应用中，选择哪种优化器应结合具体问题；
同时，优化器的选择也取决于使用者对优化器的熟悉程度（比如参数的调节等等）。

**梯度和学习率：**保证优化方向和迈的步子大小

优化器的步骤基本都是以上流程，差异体现在第一步和第二步上。
SGD没有利用动量，
MSGD在SGD基础上增加了一阶动量，
AdaGrad、AdaDelta和RMSProp法在SGD基础上增加了二阶动量。
Adam把一阶动量和二阶动量都用起来了。——Adam更好吧！

SGD和Adam谁收敛的比较快？谁能达到全局最优解？

SGD算法没有动量的概念，SGD和Adam相比，缺点是下降速度慢，对学习率要求严格。

而Adam引入了一阶动量和二阶动量，下降速度比SGD快，
Adam可以自适应学习率，所以初始学习率可以很大。

SGD相比Adam，更容易达到全局最优解。
主要是后期Adam的学习率太低，影响了有效的收敛。

我们可以前期使用Adam，后期使用SGD进一步调优。————牛啊！！！

adam用到二阶矩的原理是什么

Adam法本质上是带有动量项的RMSProp法，它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。
二阶矩的原理是：引入二阶动量，根据训练轮数的不同，对学习率进行了动态调整：

Batch的大小如何选择，过大的batch和过小的batch分别有什么影响

Batch选择时尽量采用2的幂次，如8、16、32等

在合理范围内，增大Batch_size的好处：
（1）提高了内存利用率以及大矩阵乘法的并行化效率。
（2）减少了跑完一次epoch(全数据集）所需要的迭代次数，加快了对于相同数据量的处理速度。

盲目增大Batch_size的坏处：
（1）提高了内存利用率，但是内存容量可能不足。
（2）跑完一次epoch(全数据集)所需的迭代次数减少，要想达到相同的精度，其所花费的时间大大增加，从而对参数的修正也就显得更加缓慢。
（3）Batch_size增大到一定程度，其确定的下降方向已经基本不再变化。

Batch_size过小的影响：
（1）训练时不稳定，可能不收敛
（2）精度可能更高。

梯度下降的思想

梯度下降法是原始的优化方法，
梯度下降的核心思想：负梯度方向是使函数值下降最快的方向，因此我们的目标就是求取目标函数的负梯度。

在梯度下降法中，因为每次都**遍历了完整的训练集，**其能保证结果为全局最优（优点），但是也因为我们需要对于每个参数求偏导，且在对每个参数求偏导的过程中还需要对训练集遍历一次，当训练集很大时，计算费时（缺点）。

后面一堆改进，加动量，一阶矩估计，二阶矩估计，动态自适应调整学习率，越来越稳定，快速。

---

总结

提示：重要经验：

1）优化器实际上就是从梯度下降开始的优化历程，后面一堆改进，加动量，一阶矩估计，二阶矩估计，动态自适应调整学习率，越来越稳定，快速。
2）深度学习，机器学习的这些知识点，都不是零碎的，都是有前后优化的逻辑的，前面有缺陷，后面大家慢慢改进，然后形成一个体系，到现在有很多成熟优秀的解决方案在这用。
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。