Trie树(前缀树、字典树)
目录
什么是前缀树
前缀树的优缺点:
前缀树的应用
什么是前缀树
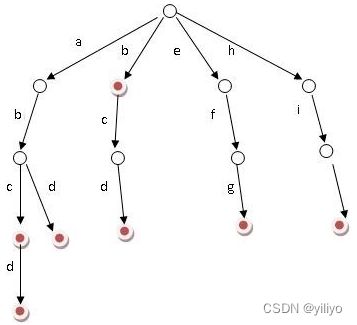
Trie树,即字典树,又称单词查找树或键树,是一种多叉树结构,是一种哈希树的变种。典型应用是用于统计和排序大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:最大限度地减少无谓的字符串比较。如下图:
好比假设有b,abc,abd,bcd,abcd,efg,hii 这6个单词,那我们创建trie树就得到
上图可以归纳出 Trie 树的基本性质:
1. 根节点不包含字符,除根节点外的每一个子节点都包含一个字符。
2. 从根节点到某一个节点,路径上经过的字符连接起来,为该节点对应的字符串。
3. 每个节点的所有子节点包含的字符互不相同。
4. 若实现前缀树时用的是hash数组,如vector
若实现前缀树时用的是标准库hashmap:unordered_map
通常在实现的时候,会在节点结构中设置一个标志,用来标记该结点处是否构成一个单词(关键字)。
可以看出,Trie 树的关键字一般都是字符串,而且 Trie 树把每个关键字保存在一条路径上,而不是一个结点中。另外,两个有公共前缀的关键字,在 Trie 树中前缀部分的路径相同,所以 Trie 树又叫做前缀树(Prefix Tree)。
前缀树的优缺点
Trie 树的核心思想是空间换时间,利用字符串的公共前缀来减少无谓的字符串比较以达到提高查询效率的目的。
优点:
- 存储和查询的都很高效,都为
O(m),其中m是待插入/查询的字符串的长度。常用于:- 向前缀树中插入字符串word;
- 查询前缀串prefix是否为已经插入到前缀树中的任意一个字符串word的前缀;
-
Trie 树中不同的关键字不会产生冲突。
-
Trie 树只有在允许一个关键字关联多个值的情况下才有类似 hash 碰撞发生。
-
Trie 树不用求 hash 值,对短字符串有更快的速度。通常,求 hash 值也是需要遍历字符串的。
-
Trie 树可以对关键字按字典序排序(需要用hash数组实现)。
缺点:
-
当 hash 函数很好时,Trie 树的查找效率会低于哈希搜索。
-
空间消耗比较大。
前缀树的应用
1,字符串检索
检索/查询功能是Trie树最原始的功能,给定一组字符串,查找某个字符串是否出现过。
思路就是从根节点开始一个一个字符进行比较:
(1) 如果沿路比较,发现不同的字符,则表示该字符串在集合中不存在。
(2) 如果所有的字符全部比较完并且全部相同,还需判断最后一个节点的标志位(标记该节点是否代表一个关键字)。
2,词频统计
Trie树常被搜索引擎系统用于文本词频统计 。
思路: 用整型变量 count 来计数。对每一个关键字执行插入操作,若已存在,计数加1,若不存在,插入后 count 置1。
3,字符串排序
Trie 树可以对大量字符串按字典序进行排序,思路也很简单:遍历一次所有关键字,将它们全部插入 Trie 树,树的每个结点所有子节点很显然地按照字母表排序,然后先序遍历输出 Trie 树中所有关键字即可。
4,前缀匹配
例如:找出一个字符串集合中所有以 ab 开头的字符串。我们只需要用所有字符串构造一个 Trie 树,然后输出以 a->b-> 开头的路径上的关键字即可。
Trie 树前缀匹配常用于搜索提示。如当输入一个网址,可以自动搜索出可能的选择。当没有完全匹配的搜索结果,可以返回前缀最相似的可能。
前缀树基本结构及实现:
// 字典树 -- hash 数组实现
// 不释放内存版
// 法1:树本身就是节点
class Trie {
public:
Trie() : child(26) , isEnd(false) {
}
void insert(string word) {
Trie* node = this;
for (auto ch : word) {
ch -= 'a';
if (node->child[ch] == nullptr) {
node->child[ch] = new Trie;
}
node = node->child[ch];
}
node->isEnd = true;
}
bool search(string word) {
Trie* matchNode = SearchPrefix(word);
return matchNode != nullptr && matchNode->isEnd;
}
bool startsWith(string prefix) {
Trie* matchNode = SearchPrefix(prefix);
return matchNode != nullptr ? true : false;
}
private:
vector child; // hash数组足额申请26节点内存, 可使子节点有序
bool isEnd;
Trie* SearchPrefix(string word)
{
Trie* node = this;
for (auto ch : word) {
ch -= 'a';
if (node->child[ch] == nullptr) {
return nullptr;
}
node = node->child[ch];
}
return node;
}
};
// 法2:树本身只包含根节点,节点结构在树外部实现
namespace TrieTest1 {
struct Node {
vector child; // hash数组足额申请26节点内存, 可使子节点有序
Node() : child(26), isEnd(false) {};
bool isEnd;
};
class Trie {
public:
Trie() {}
void insert(string word) {
Node* node = &root;
for (auto ch : word) {
ch -= 'a';
if (node->child[ch] == nullptr) {
node->child[ch] = new Node;
}
node = node->child[ch];
}
node->isEnd = true;
}
bool search(string word) {
Node* matchNode = SearchPrefix(word);
return matchNode != nullptr && matchNode->isEnd;
}
bool startsWith(string prefix) {
Node* matchNode = SearchPrefix(prefix);
return matchNode != nullptr ? true : false;
}
private:
Node root;
Node* SearchPrefix(string word) {
Node* node = &root;
for (auto ch : word) {
ch -= 'a';
if (node->child[ch] == nullptr) {
return nullptr;
}
node = node->child[ch];
}
return node;
}
};
}; // 释放内存版
// 树内部用pool记录所有申请过的节点指针,析构函数中遍历释放
namespace TrieTest2 {
struct Node {
vector child;
Node() : child(26), isEnd(false) {};
bool isEnd;
};
class Trie {
public:
Trie() {}
~Trie()
{
for (auto& nodePtr : pool) {
delete nodePtr;
}
}
void insert(string word) {
Node* node = &root;
for (auto ch : word) {
ch -= 'a';
if (node->child[ch] == nullptr) {
node->child[ch] = new Node;
pool.push_back(node->child[ch]);
}
node = node->child[ch];
}
node->isEnd = true;
}
bool search(string word) {
Node* matchNode = SearchPrefix(word);
return matchNode != nullptr && matchNode->isEnd;
}
bool startsWith(string prefix) {
Node* matchNode = SearchPrefix(prefix);
return matchNode != nullptr ? true : false;
}
private:
vector pool;
Node root;
Node* SearchPrefix(string word)
{
Node* node = &root;
for (auto ch : word) {
ch -= 'a';
if (node->child[ch] == nullptr) {
return nullptr;
}
node = node->child[ch];
}
return node;
}
};
}; // 前缀树--hashmap实现
namespace TrieTest3 {
struct Node {
unordered_map child; // 按存在的子节点申请内存, 子节点无序
bool isEnd = false;
};
class Trie {
public:
Trie() {}
void insert(string word) {
Node* node = &root;
for (auto ch : word) {
if (node->child.count(ch) == 0) {
node->child[ch] = new Node;
}
node = node->child[ch];
}
node->isEnd = true;
}
bool search(string word) {
Node* matchNode = SearchPrefix(word);
return matchNode != nullptr && matchNode->isEnd;
}
bool startsWith(string prefix) {
Node* matchNode = SearchPrefix(prefix);
return matchNode != nullptr ? true : false;
}
private:
Node root;
Node* SearchPrefix(string word)
{
Node* node = &root;
for (auto ch : word) {
if (node->child.count(ch) == 0) {
return nullptr;
}
node = node->child[ch];
}
return node;
}
};
}; 1,字符串检索 + 4,前缀匹配
208. 实现 Trie (前缀树)
如上前缀树基本结构及实现解法。
648. 单词替换
思路:直接replace了原始串中前缀词。
另一种解法是把原始串每个单词放入一个vector,用一个string res记录拼接结果,遍历vector若匹配了前缀,则用前缀拼接在res,否则用原单词拼接在res。
struct Node {
bool isEnd;
string key;
vector child;
Node() : child(26), isEnd(false) {};
};
class Trie {
public:
void AddNode(string &word)
{
Node* node = &trieRoot;
for (auto ch : word) {
ch -= 'a';
if (node->child[ch] == nullptr) {
node->child[ch] = new Node;
}
node = node->child[ch];
}
node->isEnd = true;
node->key = word;
}
Node* Search(string &word)
{
Node* node = &trieRoot;
for (auto ch : word) {
ch -= 'a';
if (node->child[ch] == nullptr) {
return node;
}
node = node->child[ch];
if (node->isEnd) {
return node;
}
}
return node;
}
private:
Node trieRoot;
};
class Solution {
public:
string replaceWords(vector& dictionary, string sentence) {
// 构建前缀树
Trie trie;
for (auto & word : dictionary) {
trie.AddNode(word);
}
string eachWord;
auto start = sentence.begin();
for (auto start = sentence.begin(); start != sentence.end();) {
if (isspace(*start)) {
start++;
}
auto wordEnd = find_if_not(start, sentence.end(), ::isalpha);
string eachWord(start, wordEnd);
Node* node = trie.Search(eachWord);
if (!node->isEnd) {
start = wordEnd;
continue;
}
string prefix = node->key;
int len = distance(sentence.begin(), start);
sentence.replace(start, wordEnd, prefix);
start = sentence.begin() + len + prefix.size();
}
return sentence;
}
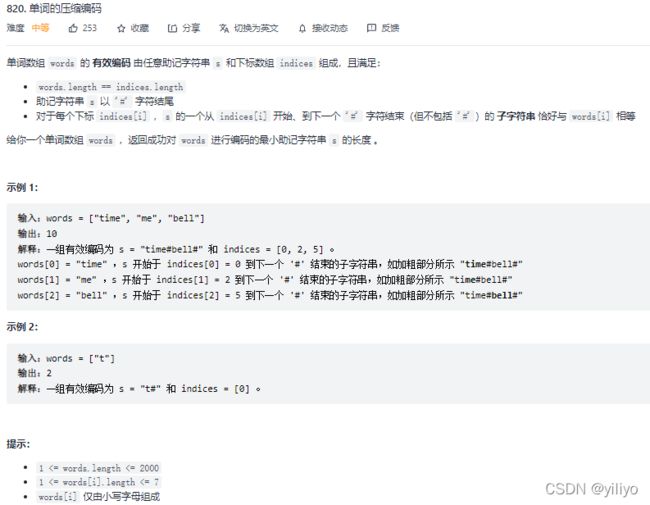
}; 820. 单词的压缩编码
思路:对words中每个word反转(["emit", "em", "lleb"]),并构建前缀树,把前缀树从根到叶上的word累加长度。
在统计Trie树中从根到叶节点word时有三种方法:(时间复杂度都是![]() ,法1耗时稍高,因为dfs又进行了一遍
,法1耗时稍高,因为dfs又进行了一遍![]() 的耗时) 。
的耗时) 。
法1:Trie树的每个node中用unordered_map记录child,对Trie进行dfs累加每个叶节点的深度,孩子节点为空时就是叶节点。
struct Node {
//string key;
unordered_map child;
};
class Trie {
public:
void AddNode(string &word)
{
Node* node = &trieRoot;
for (int i = word.size() - 1; i >= 0; i--) {
if (node->child.count(word[i]) == 0) {
node->child[word[i]] = new Node;
}
node = node->child[word[i]];
//node->key = word;
}
}
Node trieRoot;
};
class Solution {
public:
int minimumLengthEncoding(vector& words) {
// 构建trie
Trie trie;
for (auto& word : words) {
trie.AddNode(word);
}
Dfs(&trie.trieRoot, 0);
return res;
}
void Dfs(Node* node, int depth)
{
if (node->child.empty()) {
//res += node->key.size() + 1; // 1 means '#'
res += depth + 1;
return;
}
for (auto& node : node->child) {
Dfs(node.second, depth + 1);
}
}
private:
int res = 0;
}; 法2(官网解答):Trie树的每个node中用hash vector还是hashmap记录child不重要,重要的是用count直接记录该node的孩子节点数量。在遍历words,构建Trie树时,用insert返回word的最后node和word在words中的idx一起记录在一个map中。对没有孩子节点的node的word累加长度。
struct Node2 {
vector child;
int count = 0; // 本节点的孩子数, 孩子数为0,说明是叶节点也即是最长串
Node2() : child(26) {};
};
class Trie2 {
public:
Node2* insert(string &word)
{
Node2* node = &trieRoot;
for (int i = word.size() - 1; i >= 0; i--) {
char ch = word[i] - 'a';
if (node->child[ch] == nullptr) {
node->child[ch] = new Node2;
node->count++;
}
node = node->child[ch];
}
return node;
}
Node2 trieRoot;
};
class Solution2 {
public:
int minimumLengthEncoding(vector& words) {
unordered_map wordNodeIdxMap; // 记录每个word在Trie中最后node及其在原数组对应的idx
int res = 0;
// 构建trie
Trie2 trie;
for (int i = 0; i < words.size(); i++) {
Node2* node = trie.insert(words[i]);
wordNodeIdxMap[node] = i;
}
// 对无孩子的叶节点长度统计
for (auto& ele : wordNodeIdxMap) {
if (ele.first->count == 0) {
res += words[ele.second].size() + 1;
}
}
return res;
}
}; 法3(甜姨解答):先对words进行按字符串长度从长到短排序,这样构建Trie树时,保证长word先构建好从根到叶的路径,后面的短子串在入Trie时肯定不能构建出一条新路径了。insert方法直接返回每条新路径对应word的长度,并累加。
注:string/vector等容器的size()是O(1),但是list的size()方法可能是O(n)(跟gcc版本、是否-std=c++11及D_GLIBCXX_USE_CXX11_ABI宏有关STL 容器的 size() 方法的时间复杂度是多少? - 知乎)
struct TrieNode {
vector child;
TrieNode() : child(26) {};
};
class Trie1 {
public:
int insert(string& word)
{
int len = 0;
TrieNode* node = &root;
bool isNew = false;
for (int i = word.size() - 1; i >= 0; i--) {
if (node->child[word[i] - 'a'] == nullptr) {
isNew = true;
node->child[word[i] - 'a'] = new TrieNode;
}
node = node->child[word[i] - 'a'];
}
return isNew == true ? word.size() + 1 : 0;
}
private:
TrieNode root;
};
class Solution1 {
public:
int minimumLengthEncoding(vector& words) {
sort(words.begin(), words.end(), [](string &s1, string &s2) {return s1.size() > s2.size();});
// 构建trie
Trie1 trie;
int res = 0;
for (auto& word : words) {
res += trie.insert(word);
}
return res;
}
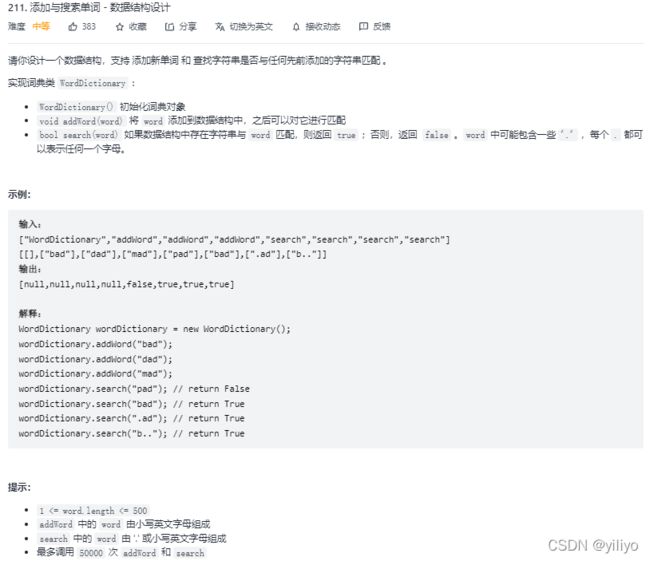
}; 211. 添加与搜索单词 - 数据结构设计
思路:前缀树 + dfs。dfs时根据当前word[start],若为字母,则候选集就下一个node,若为'.',则候选集为child数组。
struct Node {
vector child;
int childCnt = 0;
bool isEnd = false;
Node() : child(26) {};
};
class WordDictionary {
public:
WordDictionary() {
}
void addWord(string word) {
Node* node = &root;
for (auto ch : word) {
ch -= 'a';
if (node->child[ch] == nullptr) {
node->child[ch] = new Node;
node->childCnt++;
}
node = node->child[ch];
}
node->isEnd = true;
}
bool search(string word) {
int start = 0;
bool res = BackTrack(word, start, &root);
return res;
}
// dfs
bool BackTrack(string& word, int start, Node* node)
{
if (start == word.size()) {
if (node->isEnd == true || node->childCnt == 0) {
return true;
} else {
return false;
}
}
// 大剪枝
if (node->childCnt == 0) {
return false;
}
// word[start]为字母
if (word[start] != '.' && node->child[word[start] - 'a'] == nullptr) {
return false;
}
if (word[start] != '.' && node->child[word[start] - 'a'] != nullptr) {
if (BackTrack(word, start + 1, node->child[word[start] - 'a'])) {
return true;
}
}
// word[start]为'.'
for (int i = 0; i < 26; i++) {
if (word[start] == '.' && node->child[i] != nullptr) {
if (BackTrack(word, start + 1, node->child[i])) {
return true;
}
}
}
return false;
}
private:
Node root;
}; 212. 单词搜索 II
// 思路1:遍历words + board_backtrack
算法:见lc79
时间复杂度: O(words.length) * O(mn * 3^(words[i].length)) = 3 * 10^4 * 12 *12 * 3^10 = 255,091,680,000
// 思路2:boards_backtrack + words_Trie
算法:回溯到某pos时,不要用从起始点到pos的整个串到Trie中搜前缀串,而是回溯的过程中把Trie的node带到递归调用中。
候选集:四个方向
终止条件:当前pos不是words中任意单词的前缀,需要return(剪枝)
收敛条件:当前pos是words中的一个单词,即node的isEnd为true,不需要return,继续检查pos后续的路径是否能匹配words中的一个其他单词
时间复杂度:回溯的时间复杂度O(mn * 3^(words[i].length)) * searchTrie的时间复杂度O(1) = 12 *12 * 3^10 = 8,503,056
// 思路2优化:边回溯边删除Trie的叶节点, 来缩小Trie上的节点数
思路和算法
考虑以下情况。假设给定一个所有单元格都是 a 的二维字符网格和单词列表 ["a", "aa", "aaa", "aaaa"] 。当我们使用方法一来找出所有同时
在二维网格和单词列表中出现的单词时,我们需要遍历每一个单元格的所有路径,会找到大量重复的单词。
为了缓解这种情况,我们在回溯的恢复现场阶段判断如果刚刚回溯回来的node是叶节点(若是原始完整路径的叶节点h(o->a->t->h),
说明完整路径是一个word,那么该完整路径word在回溯之前已经记录在resSet中,为了避免从其他起始pos'o',重复遍历o->->t->h重复记录到resSet,所以删除该叶节点h;
若是非完整路径叶节点t(o->a->t),那么oat也不是words中的word,也可删除该叶节点t),
进行释放内存后删除,来缩小Trie节点数。
struct Node {
vector child;
int childCnt = 0;
bool isEnd = false;
string key;
Node() : child(26) {};
};
class Trie {
public:
void insert(const string& word) {
Node* node = &root;
for (auto ch : word) {
ch -= 'a';
if (node->child[ch] == nullptr) {
node->child[ch] = new Node;
node->childCnt++;
}
node = node->child[ch];
}
node->isEnd = true;
node->key = word;
}
Node root;
};
// 思路2:boards_backtrack + words_Trie // 936ms, 41%
class Solution {
public:
vector findWords(vector>& board, vector& words) {
Trie trie;
for (auto& word : words) {
trie.insert(word);
}
unordered_set resSet;
vector> dirs = {{0, 1}, {0, -1}, {-1, 0}, {1, 0}};
vector> visited(board.size(), vector(board[0].size(), false));
for (int i = 0; i < board.size(); i++) {
for (int j = 0; j < board[0].size(); j++) {
BackTrack(i, j, board, &trie.root, dirs, visited, resSet);
}
}
return vector(resSet.begin(), resSet.end());
}
private:
void BackTrack(int curL, int curC, vector>& board, Node* node, vector>& dirs,
vector>& visited, unordered_set& resSet)
{
// 终止条件
if (node->child[board[curL][curC] - 'a'] == nullptr) {
return;
}
// 收敛条件
if (node->child[board[curL][curC] - 'a']->isEnd == true) {
resSet.insert(node->child[board[curL][curC] - 'a']->key);
}
visited[curL][curC] = true;
// 遍历候选集
for (auto& dir : dirs) {
int nextL = curL + dir[0];
int nextC = curC + dir[1];
if (nextL < 0 || nextL >= board.size() || nextC < 0 || nextC >= board[0].size() || visited[nextL][nextC]) {
continue;
}
BackTrack(nextL, nextC, board, node->child[board[curL][curC] - 'a'], dirs, visited, resSet);
}
visited[curL][curC] = false;
}
};
// 思路2优化:边回溯边删除Trie的叶节点, 来缩小Trie上的节点数 316ms 73.95%
class Solution1 {
public:
vector findWords(vector>& board, vector& words) {
Trie trie;
for (auto& word : words) {
trie.insert(word);
}
unordered_set resSet;
vector> dirs = {{0, 1}, {0, -1}, {-1, 0}, {1, 0}};
vector> visited(board.size(), vector(board[0].size(), false));
for (int i = 0; i < board.size(); i++) {
for (int j = 0; j < board[0].size(); j++) {
BackTrack(i, j, board, &trie.root, dirs, visited, resSet);
}
}
return vector(resSet.begin(), resSet.end());
}
private:
void BackTrack(int curL, int curC, vector>& board, Node* node, vector>& dirs,
vector>& visited, unordered_set& resSet)
{
// 终止条件
if (node->child[board[curL][curC] - 'a'] == nullptr) {
return;
}
// 收敛条件
if (node->child[board[curL][curC] - 'a']->isEnd == true) {
resSet.insert(node->child[board[curL][curC] - 'a']->key);
}
// 遍历候选集
if (node->child[board[curL][curC] - 'a']->childCnt != 0) { // 这里的判断可写可不写,因为若childCnt == 0,则在接下来的回溯递归BackTrack的终止条件处这返回
visited[curL][curC] = true;
for (auto& dir : dirs) {
int nextL = curL + dir[0];
int nextC = curC + dir[1];
if (nextL < 0 || nextL >= board.size() || nextC < 0 || nextC >= board[0].size() || visited[nextL][nextC]) {
continue;
}
BackTrack(nextL, nextC, board, node->child[board[curL][curC] - 'a'], dirs, visited, resSet);
}
visited[curL][curC] = false;
}
// 删除Trie的叶节点
if (node->child[board[curL][curC] - 'a']->childCnt == 0) {
delete node->child[board[curL][curC] - 'a'];
node->child[board[curL][curC] - 'a'] = nullptr;
}
}
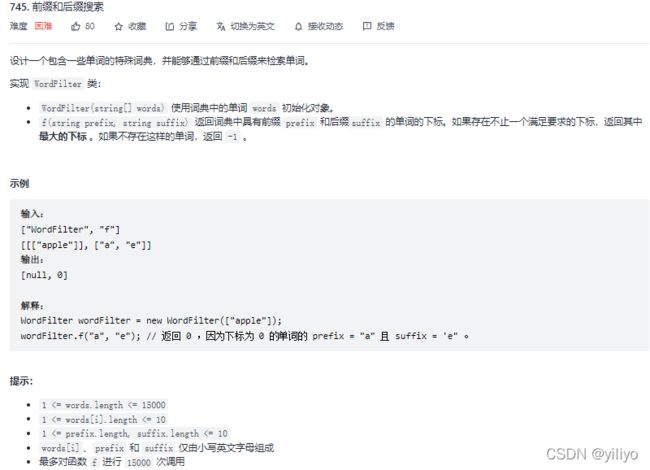
}; 745. 前缀和后缀搜索
方法1:单独的前、后缀树 + hashmap
思路:
(1) 前缀树用于构建和查找prefix,后缀树用于构建和查找suffix。
(2)构建树时,每个node用vector
(3)用3个hashmap记录已经找到的(prefix+“#” + suffix)、prefix、suffix,避免重复查找。
时间复杂度:O(NK + Q(Nlog(N)+K))。其中N指的是单词的个数,K指的是单词中的最大长度,Q指的是搜索的次数。
优化第(2)步中从两个idxVec1和idxVec2找公共最大算法:
由于构建树时每个node中添加words中单词索引是正序添加的,因此索引在idxVec中越排在后面就越大因此,我们同时倒序遍历idxVec1和idxVec2
优化后时间复杂度:O(NK + Q(N+K))。其中N指的是单词的个数,K指的是单词中的最大长度,Q指的是搜索的次数。
优化前代码:(优化后的略)。优化前实际效果(应该是用例用有大量重复的prefix和suffix,用map找到后直接返回了,若不用map记录,则超时):
执行用时: 444 ms, 49%
内存消耗: 153.5 MB,57%
struct Node {
bool isEnd;
vector idxVec;
vector child;
Node() : child(26), isEnd(false) {};
};
class Trie {
public:
void AddNode(string &word, int idx)
{
Node* preNode = &prefixRoot;
for (auto ch : word) {
ch -= 'a';
if (preNode->child[ch] == nullptr) {
preNode->child[ch] = new Node;
}
preNode = preNode->child[ch];
preNode->idxVec.push_back(idx);
}
preNode->isEnd = true;
Node* subNode = &suffixRoot;
for (int i = word.size() - 1; i >= 0; i--) {
if (subNode->child[word[i] - 'a'] == nullptr) {
subNode->child[word[i] - 'a'] = new Node;
}
subNode = subNode->child[word[i] - 'a'];
subNode->idxVec.push_back(idx);
}
subNode->isEnd = true;
}
vector SearchPrefix(string &prefix)
{
Node* node = &prefixRoot;
for (auto ch : prefix) {
ch -= 'a';
if (node->child[ch] == nullptr) {
return {};
}
node = node->child[ch];
}
return node->idxVec;
}
vector SearchSuffix(string &suffix)
{
Node* node = &suffixRoot;
for (int i = suffix.size() - 1; i >= 0; i--) {
if (node->child[suffix[i] - 'a'] == nullptr) {
return {};
}
node = node->child[suffix[i] - 'a'];
}
return node->idxVec;
}
private:
Node prefixRoot;
Node suffixRoot;
};
class WordFilter {
public:
WordFilter(vector& words) {
for (int i = 0; i < words.size(); i++) {
trie.AddNode(words[i], i);
}
}
int f(string prefix, string suffix) {
string tmpstr = prefix + "##" + suffix;
if (mp.count(tmpstr)) {
return mp[tmpstr];
}
vector preIdxVec;
if (prefixMap.count(prefix)) {
preIdxVec = prefixMap[prefix];
} else {
preIdxVec = trie.SearchPrefix(prefix);
prefixMap.insert({prefix, preIdxVec});
}
vector subIdxVec;
if (suffixMap.count(suffix)) {
subIdxVec = suffixMap[suffix];
} else {
subIdxVec = trie.SearchSuffix(suffix);
suffixMap.insert({suffix, subIdxVec});
}
copy(subIdxVec.begin(), subIdxVec.end(), back_inserter(preIdxVec));
sort(preIdxVec.begin(), preIdxVec.end());
for (int i = preIdxVec.size() - 1; i > 0; i--) {
if (preIdxVec[i] == preIdxVec[i - 1]) {
mp[tmpstr] = preIdxVec[i];
return preIdxVec[i];
}
}
mp[tmpstr] = -1;
return -1;
}
Trie trie;
private:
unordered_map mp;
unordered_map> prefixMap;
unordered_map> suffixMap;
}; 方法2:后缀修饰的单词查找树
时间复杂度:O(NK^2 + QK)。其中 NN 指的是单词的个数,KK 指的是单词中的最大长度,Q 指的是搜索的次数。
执行用时: 412 ms,53%
内存消耗: 188.7 MB,32%
namespace sol2 {
struct Node {
int maxIdx;
vector child;
Node() : child(27), maxIdx(-1) {};
};
class Trie {
public:
void AddNode(vector& words)
{
for (int idx = 0; idx < words.size(); idx++) {
string word = words[idx] + "#";
for (int i = 0; i < word.size(); i++) {
Node* node = &root;
for (int j = i; j < 2 * word.size() - 1; j++) {
int k = word[j % word.size()] == '#' ? 26 : word[j % word.size()] - 'a';
if (node->child[k] == nullptr) {
node->child[k] = new Node;
}
node = node->child[k];
node->maxIdx = idx;
}
}
}
}
int SearchPrefix(string &prefix, string &suffix)
{
string fullStr = suffix + "#" + prefix;
Node* node = &root;
for (auto ch : fullStr) {
ch = ch == '#' ? 26 : ch - 'a';
if (node->child[ch] == nullptr) {
return -1;
}
node = node->child[ch];
}
return node->maxIdx;
}
private:
Node root;
};
class WordFilter {
public:
WordFilter(vector& words) {
trie.AddNode(words);
}
int f(string prefix, string suffix) {
return trie.SearchPrefix(prefix, suffix);
}
private:
Trie trie;
};
} 720. 词典中最长的单词
// 方法:字典树
// 思路:构建字典树,遍历时只筛选每个node都是end的节点(即是上个node添加一个字母得来的node),到了叶节点仅需比较长度,用长度大的更新res,因为相等长度的已经是字典序,无需更新res。
struct Node {
vector child;
bool isleaf = false;
string str;
Node() : child(26) {}
};
class Trie {
public:
void Insert(string& word)
{
Node* node = &root;
for (auto ch : word) {
if (node->child[ch - 'a'] == nullptr) {
node->child[ch - 'a'] = new Node;
}
node = node->child[ch - 'a'];
}
node->isleaf = 1;
node->str = word;
}
Node root;
};
class Solution {
public:
void dfs(Node* node, string& res)
{
if (node == nullptr) {
return;
}
if (!node->isleaf) {
return;
}
if (node->str.size() > res.size()) { // 只需要比较长度, 在长度相等时因为字典遍历能保证字典序
res = node->str;
}
for (auto ele : node->child) {
dfs(ele, res);
}
}
string longestWord(vector& words) {
Trie trie;
for (auto& word : words) {
trie.Insert(word);
}
string res;
for (auto node : trie.root.child) {
dfs(node, res);
}
return res;
}
}; 参考:
数据结构与算法:字典树(前缀树) - 知乎