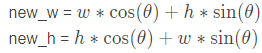基于Opencv c++图像三维空间旋转（使用二维旋转、缩放进行代替的方式---思路转换）

针对于图像的三维旋转，看了很多博客，一般的变换都是基于刚性变换、相似变换、仿射变换、透射变换，而真正的基于图像的三维旋转却是很少的。当然真正的图像实现三维旋转的过程是可以使用PPT进行一个演示的，PPT之中可以设定针对与x轴、y轴、z轴进行三维旋转变换的过程。

这是是提供一个思路，使用一般的变换代替三维旋转的过程，从而提取出来有效的信息。

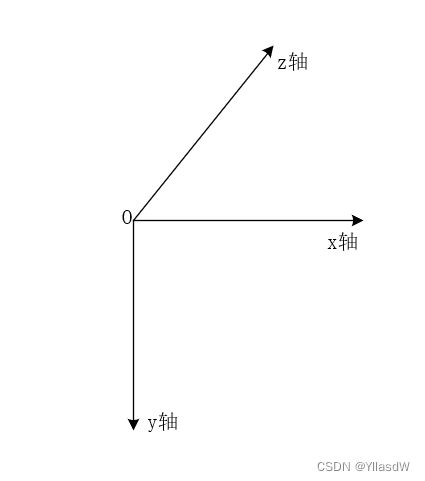
真正的图片三维旋转的过程之中，是围绕图中三个坐标轴进行旋转的过程，但是opencv之中没有关于x轴、y轴进行旋转的方式代码的整理。为了提取出围绕x轴、y轴之中的信息，可以使用缩放的想法去替代旋转，当然，这种思路会影响图片旋转过程之中的直观感受，但是图片信息并不会丢失。

围绕x轴旋转---右手大拇指指向轴向正方向，其余四指指向旋转正方向

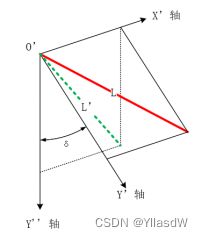
举个栗子：原始图片围绕x轴旋转30度，由于相机之中显示的图片是一个二维图片，z轴是不存在的.可以想像一下实际的空间之中，x轴的坐标是不发生变化的，y轴的坐标缩小为原来的cos30°。并不影响原来的信息丢失。

就像上图之中L的斜率，原来是k，之后就变成了kcos15°，原始信息会根据旋转的变化而发生变化。这里应当特别注意，这种方式只是适合对于在实际坐标系之中的小角度的变换，并且在转换前后是不存在歧义性的时候可以使用，当存在一定的歧义性是不可以使用这种方式（实际问题实际考虑）

实现原理是很好进行理解的，在竖直方向和水平方向上的像素进行一定的缩放，就是可以达到相应的一个效果，比如说水平方向上的像素不发生变化，竖直方向上的像素变成原来的cos（30）就是如下面的代码所示。

具体的的代码如下所示：看了一些代码是进行三次样条插值啥的，如果要是想要水一水论文的时候，可以使用那种比较复杂的什么插值啥的，但是下面这个是足够使用。

#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/highgui/highgui.hpp"
#include 
#include 
#include 
using namespace cv;
using namespace std;
double acos(double x);
#define PI 3.14159265
void fun1(cv::Mat& src, double kx, double ky)
{
	int  row = src.rows * kx;
	int  col = src.cols * ky;

	cv::Mat dst(row, col, src.type());
	for (int i = 0; i < row; i++)
	{
		int srx = i / kx;
		for (int j = 0; j < col; j++)
		{
			int sry = j / ky;
			dst.at(i, j) = src.at(srx, sry);
		}
	}
	cv::imwrite("C:\\Users\\td\\Desktop\\第二步\\1.相机标定（单目、双目）\\相机标定（单目、双目）\\4.png", dst);
}

void main()
{
	cv::Mat  src = cv::imread("C:\\Users\\td\\Desktop\\第二步\\1.相机标定（单目、双目）\\相机标定（单目、双目）\\Pic_1.bmp");
	fun1(src, acos(30), 1);//参数2是Y轴进行放缩的过程，参数3是x轴进行放缩的过程。
}

//实际的操作函数cos之中输入的是弧度，这里为了更好的演示，我直接这里进行转化好了
double acos(double x)
{
	return cos(x * PI / 180.0);
}

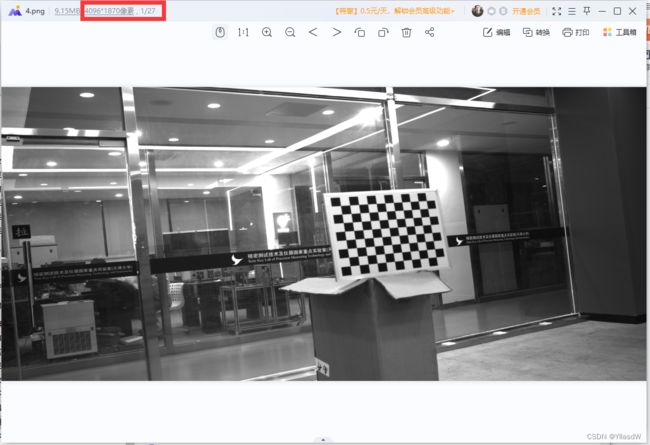
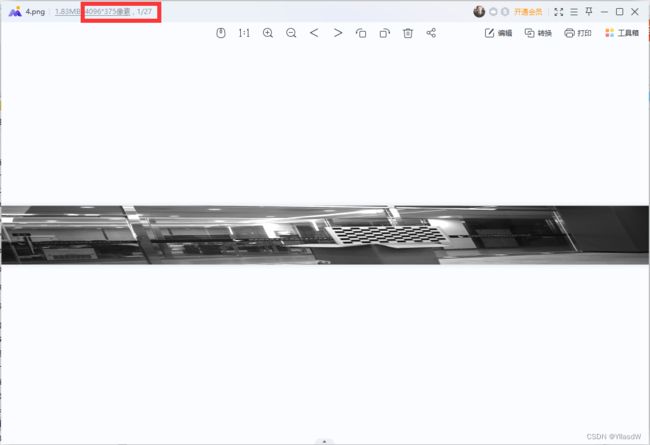
输入图像：观察到其像素关系是4096*2160

 输出图像：观察到其输出图像的像素为4096*1870

 通过竖直方向的像素可以得知，原来的2160变成了1870，也就是2160*cos（30°）约为1870，就是进行了一个转换过程，是不是通俗易懂。

围绕y轴的旋转过程是和上面的过程是类似的

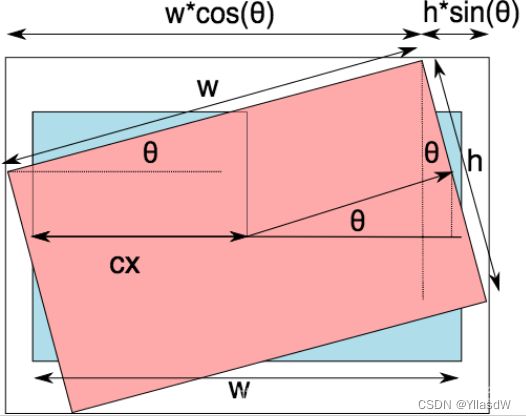
围绕z轴旋转---右手大拇指指向轴向正方向，其余四指指向旋转正方向

旋转原理如下所示：

这里我们将z轴放置在图像正中间，其效果是与放置在图像的左上角的效果是一样的。旋转代码如下所示：

#include 
#include 
#include 
#include 
using namespace cv;

void rotate_Demo(Mat& image) {
	Mat dst_0, dst_1, M;
	int h = image.rows;
	int w = image.cols;
	M = getRotationMatrix2D(Point(w / 2, h / 2), 10, 1.0);
	warpAffine(image, dst_0, M, image.size());

	double cos = abs(M.at(0, 0));
	double sin = abs(M.at(0, 1));

	int new_w = cos * w + sin * h;
	int new_h = cos * h + sin * w;
	M.at(0, 2) += (new_w / 2.0 - w / 2);
	M.at(1, 2) += (new_h / 2.0 - h / 2);
	warpAffine(image, dst_1, M, Size(new_w, new_h), INTER_LINEAR, 0, Scalar(255, 255, 0));
	namedWindow("output", WINDOW_NORMAL);
	imshow("output", dst_0);
	namedWindow("output1", WINDOW_NORMAL);
	imshow("output1", dst_1);
}

int main(int argc, char** argv) {
	Mat src = imread("C:\\Users\\td\\Desktop\\第二步\\1.相机标定（单目、双目）\\相机标定（单目、双目）\\Pic_1.bmp");
	if (src.empty()) {
		printf("Could not load images...\n");
		return -1;
	}
	namedWindow("input", WINDOW_NORMAL);
	imshow("input", src);


		
	rotate_Demo(src);

	waitKey(0);
	destroyAllWindows();
	return 0;
}

输入图像：

输出图像：

可以见到输出的图像之中output是存在原始的信息丢失的，因此，需要输出一个完整的图像，就是需要进行output1的操作。

围绕x轴旋转之后，围绕z轴旋转代码

这里围绕y轴进行旋转的过程与x轴是相同道理。因此，这里写的代码是不包含围绕y轴进行旋转的。将上述代码进行一个整合，代码是如下所示：

#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/highgui/highgui.hpp"
#include 
#include 
#include 

using namespace cv;
using namespace std;

#define PI 3.14159265

Mat fun1(cv::Mat& src, double kx, double ky);//进行围绕x轴旋转的函数
Mat rotate_Demo(Mat& image, double z);//围绕y轴进行旋转
double acos(double x);//角度转换为弧度

int main()
{
	//输入图像
	cv::Mat  src = cv::imread("C:\\Users\\td\\Desktop\\第二步\\1.相机标定（单目、双目）\\相机标定（单目、双目）\\Pic_1.bmp");
	if (src.empty()) {
		printf("Could not load images...\n");
		return -1;
	}

	//显示输入的图像
	namedWindow("input", WINDOW_NORMAL);
	imshow("input", src);

	//围绕x轴进行旋转，输出图像为rx
	Mat rx = fun1(src, acos(80), 1);//参数2是Y轴进行放缩的过程，参数3是x轴进行放缩的过程。

	//围绕z轴进行旋转，输出图像为
	Mat rz = rotate_Demo(rx, 10);

	waitKey(0);

	return 0;
}

//实际的操作函数cos之中输入的是弧度
double acos(double x)
{
	return cos(x * PI / 180.0);
}

Mat fun1(cv::Mat& src, double kx, double ky)
{
	int  row = src.rows * kx;
	int  col = src.cols * ky;

	cv::Mat dst(row, col, src.type());
	for (int i = 0; i < row; i++)
	{
		int srx = i / kx;
		for (int j = 0; j < col; j++)
		{
			int sry = j / ky;
			dst.at(i, j) = src.at(srx, sry);
		}
	}
	namedWindow("output_x", WINDOW_NORMAL);
	imshow("output_x", dst);
	cv::imwrite("C:\\Users\\td\\Desktop\\第二步\\1.相机标定（单目、双目）\\相机标定（单目、双目）\\4.png", dst);//如果要是不需要写入图片的话，这一句话是可以删掉的
	return dst;
}


Mat rotate_Demo(Mat& image,double z) {
	Mat dst_0, dst_1, M;
	int h = image.rows;
	int w = image.cols;
	M = getRotationMatrix2D(Point(w / 2, h / 2), z, 1.0);
	warpAffine(image, dst_0, M, image.size());

	double cos = abs(M.at(0, 0));
	double sin = abs(M.at(0, 1));

	int new_w = cos * w + sin * h;
	int new_h = cos * h + sin * w;
	M.at(0, 2) += (new_w / 2.0 - w / 2);
	M.at(1, 2) += (new_h / 2.0 - h / 2);
	warpAffine(image, dst_1, M, Size(new_w, new_h), INTER_LINEAR, 0, Scalar(255, 255, 0));
	namedWindow("output_z1", WINDOW_NORMAL);
	imshow("output_z1", dst_0);
	namedWindow("output1_z2", WINDOW_NORMAL);
	imshow("output1_z2", dst_1);
	return dst_1;
}

输入图像：

 经过围绕x轴旋转：见下面的像素变化，这里设定是80°，是正确的

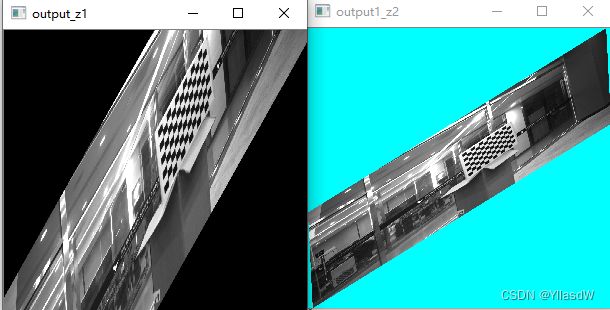
 之后围绕z轴进行旋转：

 

上述就是将围绕三维坐标轴旋转，使用二维旋转与图片相似伸缩变换进行替代的过程，将思路进行一个转化，问题就解决了。