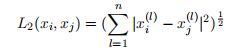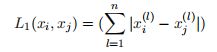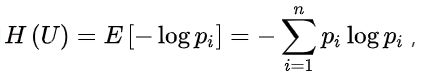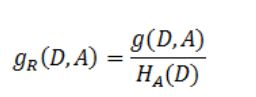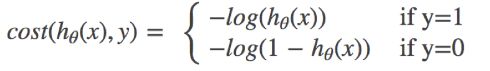机器学习算法+代码
机器学习
一、概述
1、机器学习研究方向
- 传统预测
- 图像识别
- 自然语言处理
2、数据集构成
数据集 = 特征值+目标值
监督学习:
- 目标值为类别 属于分类问题
- 目标值为连续数据 属于回归问题
无监督学习
- 无目标值
3、机器学习流程
- 获取数据
- 数据处理
- 特征工程
- 机器学习模型-训练模型
- 模型评估
- 应用
4、书籍、框架
| 机器学习 | 深度学习 | |
|---|---|---|
| 数集 | 西瓜书–周志华 | 花书 |
| 框架 | sklearn | theano、caffe2、chainer |
| 数据集 | sklearn、kaggle、UCI |
Kaggle网址:https://www.kaggle.com/datasets
UCI数据集网址: http://archive.ics.uci.edu/ml/
scikit-learn网址:[http://scikit-learn.org/stable/datasets/index.html#datasets]
二、特征工程
1、数据集
pip3 install Scikit-learn==0.19.1
from sklearn.datasets import load_**#小数据集
from sklearn.datasets import fetch_**#大数据集
1、小规模数据集
datasets.load_*()
#鸢尾花数据集
sklearn.datasets.load_iris()
#波士顿房价数据集
sklearn.datasets.load_boston()
2、大规模数据集
datasets.fetch_*(data_home=None,subset=“train”)
- data_home,表示数据集下载的目录,默认是 ~/scikit_learn_data/
- subset:train表示只要测试集;all表示全部数据都要;test表示只要测试集
3、数据集的返回值
返回值类型:datasets.base.Bunch(继承自字典)
返回值属性:
- data:特征值
- target:标签
- descr:数据描述
- feature_names:特征名
- target_names:标签名
调用返回值方式:
bunch.key = value
dict[‘key’] = value
from sklearn.datasets import load_iris
def datasets_demo():
"""
sklearn数据集的使用
:return:
"""
# 获取数据集
iris = load_iris()
print("鸢尾花数据集: \n" ,iris)
print("查看数据集描述: \n",iris['DESCR'])
print("查看数据集特征值的名字: \n",iris.feature_names)
print("查看数据集标签的名字: \n",iris.target_names)
print("查看数据集特征值: \n",iris.data.shape , iris.data)# shape:(150, 4)
return None
if __name__ == "__main__":
# 代码1:sklearn数据集使用
datasets_demo()
4、数据集划分
from sklearn.model_selection import train_test_split
机器学习一般的数据集会划分为两个部分:
- 训练数据:用于训练,构建模型
- 测试数据:在模型检验时使用,用于评估模型是否有效
sklearn.model_selection.train_test_split(arrays, *options)
-
x 数据集的特征值
-
y 数据集的标签值
-
test_size 测试集的大小,一般为float
-
random_state 随机数种子,不同的种子会造成不同的随机采样结果。相同的种子采样结果相同。
-
return 测试集特征值、训练集特征值,训练标签(目标值),测试标签(目标值)
x_train , x_test , y_train , y_test
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
def datasets_demo():
"""
sklearn数据集的使用
:return:
"""
# 获取数据集
iris = load_iris()
# print("鸢尾花数据集: \n" ,iris)
# print("查看数据集描述: \n",iris['DESCR'])
# print("查看数据.集特征值的名字: \n",iris.feature_names)
# print("查看数据集数据: \n",iris.data.shape , iris.data)# shape:(150, 4)
# 数据集的划分
x_train,x_test,y_train,y_test = train_test_split(iris.data,iris.target,test_size=0.2,random_state=22 )
print("训练集的特征值: \n",x_train,x_train.shape)
return None
if __name__ == "__main__":
# 代码1:sklearn数据集使用
datasets_demo()
2、特征工程
什么是特征工程?
专业背景知识和技巧处理数据,使得特征能在机器学习算法上发挥更好的作用的过程。(使用pandas、numpy对特征进行些处理)
特征工程内容分为三类:特征抽取、特征预处理、特征降维
1、特征抽取/特征提取
1)字典特征提取(特征离散化)
from sklearn.feature_extraction import DictVectorizer
属性
- DictVectorizer.fit_transform(X) X:字典或者包含字典的迭代器返回值:返回sparse矩阵(稀疏矩阵)
- DictVectorizer.inverse_transform(X) X:array数组或者sparse矩阵 返回值:转换之前数据格式
- DictVectorizer.get_feature_names() 返回类别名称
使用场景
- 数据类型是字典
- 数据集中存在类别特征比较多(性别、等级),先将数据集的特征转化为字典类型,然后使用DictVerctorizer进行转换
代码
from sklearn.feature_extraction import DictVectorizer
def dict_demo():
"""
字典特征抽取
:return:
"""
data = [{'city': '北京', 'temperature': 100}
, {'city': '上海', 'temperature': 60}
, {'city': '深圳', 'temperature': 30}]
# 1、实例化转换器
transfer = DictVectorizer(sparse=False)
# 2、调用fit_transform
data_new = transfer.fit_transform(data,y=None)
print("打印返回结果: \n",data_new)
if __name__ == "__main__":
dict_demo()
sparse = False
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3YarFVus-1637326542934)(https://i.loli.net/2021/11/06/fuSsliOqzFD9UVb.png)]
sparse=Ture,只表示不是0的东西,可节约内存
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JHZcLEEz-1637326542936)(https://i.loli.net/2021/11/06/VOrXlQ3s8RjC9tG.png)]
注意:数据提取类似之前pandas中的one-hot编码
2)、文本特征提取
sklearn.feature_extraction.text import CountVectorizer
1、实例化
trans = CountVectorizer(stop_words)
stop_words表示停用词,即使样本中出现但是依旧不计数的词,通常有一个停用词表。
2、方法
-
CountVectorizer.fit_transform(X)
X:文本或者包含文本字符串的可迭代对象 返回值:返回sparse矩阵
统计每个样本中特征值出现的次数
-
CountVectorizer.inverse_transform(X)
X:array数组或者sparse矩阵 返回值:转换之前数据格
-
CountVectorizer.get_feature_names() 返回值:单词列表
3、流程
- 实例化类CountVectorize
- 调用fit_transform方法输入数据并转换,注意返回格式,利用toarray()进行sparse矩阵转换array数组
sklearn.feature_extraction.text import CountVectorizer
def text_count_demo():
"""
对文本进行特征抽取,countvetorizer
:return:
"""
data = ["life is short,i like like python"
, "life is too long,i dislike python"]
# 1 实例化转换器类
transfer = CountVectorizer(stop_words=['is','like'])#stop_words:停用词
# 2 调用转换器中的方法
data_new = transfer.fit_transform(data)
print("data_new:\n",data_new.toarray())
print("array数组:\n",transfer.inverse_transform(data_new))
print("特征名字:\n",transfer.get_feature_names())
if __name__ == "__main__":
text_count_demo()
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PGkO5UzW-1637326542937)(https://i.loli.net/2021/11/07/tysLV4nuAQFwo5j.png)]
注意:此方法不支持中文,因为中文中没有空格,除非先分词
4、jieba中文分词
pip3 install jieba
from sklearn.feature_extraction.text import CountVectorizer
import jieba
def china_text_count_demo():
"""
对中文文本进行特征抽取,countvetorizer
:return:
"""
data = ["我爱北京天安门"
, "天安门上太阳升"]
# 1 实例化转换器类
transfer = CountVectorizer()
# 2 调用转换器中的方法
data_new = transfer.fit_transform(data)
print("data_new:\n",data_new.toarray())
print("array数组:\n",transfer.inverse_transform(data_new))
print("特征名字:\n",transfer.get_feature_names())
def cut_word(text):
"""
进行中文分词“我爱北京天安门 --> 我 爱 北京 天安门”
:return:
"""
a = " ".join(list((jieba.cut(text))))
print(a)
return text
def china_text_count_demo_2():
"""
中文文本特征值化,自动分词
:return:
"""
# 1 将中文文本进行分词
data = ["一种还是一种今天很残酷,明天更残酷,后天很美好,"
"但绝对大部分是死在明天晚上,所以每个人不要放弃今天。",
"我们看到的从很远星系来的光是在几百万年之前发出的,"
"这样当我们看到宇宙时,我们是在看它的过去。",
"如果只用一种方式了解某样事物,你就不会真正了解它。"
"了解事物真正含义的秘密取决于如何将其与我们所了解的事物相联系。"]
data_new = []
for sent in data:
data_new.append(cut_word(sent))
# print(data_new)
# 2 实例化countvetorizer
transf = CountVectorizer()
# 3 调用fit_transform()
data_final = transf.fit_transform(data)
print("data_final: \n",data_final)
print("特征提取结果:\n",data_final.toarray())
print("特征名字:\n",transf.get_feature_names())
return None
if __name__ == "__main__":
# 代码5 中文文本特征值提取,自动分词
china_text_count_demo_2()
# 代码6 中文分词
# cut_word("我爱北京天安门")
5、Tf-idf 提取特殊高频词(关键词)
from sklearn.feature_extraction.text import TfidfVectorizer
- 如果某个词或者短语在一篇文章中出现频率很高但是在其他文章中出现很少,那么这个词可以视为关键字
- Tf-idf用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度
定义
- 词频(term frequency,tf)指的是某一个给定的词语在该文件中出现的频率
- 逆向文档频率(inverse document frequency,idf)是一个词语普遍重要性的度量。某一特定词语的idf,可以由总文件数目除以包含该词语之文件的数目,再将得到的商取以10为底的对数得到
from sklearn.feature_extraction.text import TfidfVectorizer
import jieba
def tfidf_demo():
"""
tfidf进行文章特征提取
:return:
"""
# 1 将中文文本进行分词
data = ["一种还是一种今天很残酷,明天更残酷,后天很美好,"
"但绝对大部分是死在明天晚上,所以每个人不要放弃今天。",
"我们看到的从很远星系来的光是在几百万年之前发出的,"
"这样当我们看到宇宙时,我们是在看它的过去。",
"如果只用一种方式了解某样事物,你就不会真正了解它。"
"了解事物真正含义的秘密取决于如何将其与我们所了解的事物相联系。"]
data_new = []
for sent in data:
data_new.append(cut_word(sent))
# print(data_new)
# 2 实例化countvetorizer
transf = TfidfVectorizer(stop_words=["如果",'了解'])
# 3 调用fit_transform()
data_final = transf.fit_transform(data)
print("data_final: \n",data_final)
print("特征提取结果:\n",data_final.toarray())
print("特征名字:\n",transf.get_feature_names())
return None
if __name__ == "__main__":
# 代码7 TFidf进行文本特征提取
tfidf_demo()
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FrNevjhA-1637326542939)(C:\Users\lenovo\AppData\Roaming\Typora\typora-user-images\image-20211107113347671.png)]
3)图象特征提取(深度学习)
详情见笔记:深度学习
3、特征预处理
1、预处理
1)预处理包含内容
- 归一化
- 标准化
2)包
sklearn.preprocessing
3)意义
征的单位或者大小相差较大,或者某特征的方差相比其他的特征要大出几个数量级,容易影响(支配)目标结果,使得一些算法无法学习到其它的特征
2、归一化
定义
通过对原始数据进行变换把数据映射到(默认为[0,1])之间
min-max归一化公式:
from sklearn.preprocessing import MinMaxScaler
X ′ = x − m i n m a x − m i n X' = \frac{x-min}{max-min} X′=max−minx−min
X ′ ′ = X ′ ∗ ( m x = m i ) + m i X''=X' * (mx = mi)+ mi X′′=X′∗(mx=mi)+mi
- 此方法可以将原始数据映射到【0-1】之间
- mx,mi分别为指定区间值默认mx为1,mi为0
- max min表示此列中最大最小值
from sklearn.preprocessing import MinMaxScaler
import pandas as pd
def minmax_demo():
"""
minmax_归一化
:return:
"""
# 1 获取数据
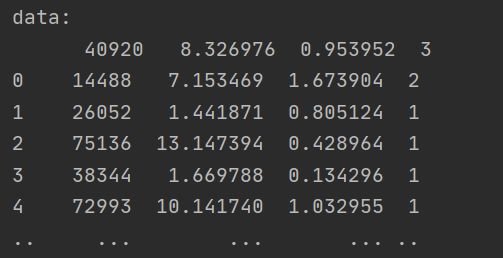
data = pd.read_table("datingTestSet2.txt")#read_csvz中会把\t都读出来
print("data:\n",data)
# 2 实例化minmaxscaler()
transf = MinMaxScaler(feature_range=[2,3])
# feature_range 表示想要把数据处理成多少区间之间的,默认0-1
# 3 调用fit_transform
data_new = transf.fit_transform(data)
print((data_new))
return None
if __name__ == "__main__":
# 代码8 minmax归一化
minmax_demo()
3、标准化
from sklearn.preprocessing import StandardScaler
意义
归一化比较容易收到最大值最小值的影响,如果出现异常值,对结果影响较大,俗称鲁棒性较差,故提出标准化,即使出现异常值,也不会影响较大。
公式
X ′ = x − m e a n σ X' =\frac{x-mean}{\sigma} X′=σx−mean
作用于每一列,mean为平均值,σ为标准差
代码
from sklearn.preprocessing import StandardScaler
def standarScaler_demo():
"""
数据标准化
:return:
"""
# 1 数据导入
data = pd.read_table("datingTestSet2.txt")
# 2 实例化standscaler
transf = StandardScaler()
# 3 fit_transform()
data_new = transf.fit_transform(data)
print("data:\n ",data_new)
if __name__ == "__main__":
# 代码9 数据标准化
standarScaler_demo()
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NmMHR2Ib-1637326542944)(https://i.loli.net/2021/11/07/B83tjmgeQApnbF5.png)]
4、特征降维
**降维是指在某些限定条件下,降低随机变量(特征)个数,得到一组“不相关”主变量的过程。(相关特征:两个有关系的特征,例如湿度与降雨量)
1、降维方式一–特征选择
(1)定义
数据中包含冗余或无关变量(或称特征、属性、指标等),旨在从原有特征中找出主要特征。
(2)方法
- Filter(过滤式):主要探究特征本身特点、特征与特征和目标值之间关联
- 方差选择法:低方差特征过滤
- 相关系数:特征与特征之间的相关程度
- Embedded (嵌入式):算法自动选择特征(特征与目标值之间的关联)
- 决策树:信息熵、信息增益
- 正则化:L1、L2
- 深度学习:卷积等
(3)模块
from sklearn.feature_selection import VarianceThreshold
2、征选择方式一 过滤式
删除低方差的一些特征,前面讲过方差的意义。再结合方差的大小来考虑这个方式的角度。
- 特征方差小:某个特征大多样本的值比较相近
- 特征方差大:某个特征很多样本的值都有差别
API
- sklearn.feature_selection.VarianceThreshold(threshold = 0.0)
- 删除所有低方差特征
- Variance.fit_transform(X)
- X:numpy array格式的数据[n_samples,n_features]
- 返回值:训练集差异低于threshold的特征将被删除。默认值是保留所有非零方差特征,即删除所有样本中具有相同值的特征。
from sklearn.feature_selection import VarianceThreshold
def variance_demo():
"""
过滤式处理低方差
:return:
"""
# 1 导入数据集
data = pd.read_csv("factor_returns.csv")
# 2 实例化VarianceThreshold转换器
transfer = VarianceThreshold(threshold=11)
#threshold表示设置的阈值,我们可以把小于这个阈值的删除,即为删除相关性比较强的内容
# 3 调用 fit_transform
data_new = transfer.fit_transform(data.iloc[:,1:-2])
print("data\n",data_new)
print("形状\n",data_new.shape)
print("原来形状\n",data.shape)
return None
if __name__ == "__main__":
# 代码10 低方差过滤
variance_demo()
data
[[ 5.95720000e+00 8.52525509e+10 8.00800000e-01 ... 1.21144486e+12
2.07014010e+10 1.08825400e+10]
[ 7.02890000e+00 8.41133582e+10 1.64630000e+00 ... 3.00252062e+11
2.93083692e+10 2.37834769e+10]
[-2.62746100e+02 5.17045520e+08 -5.67800000e-01 ... 7.70517753e+08
1.16798290e+07 1.20300800e+07]
...
[ 3.95523000e+01 1.70243430e+10 3.34400000e+00 ... 2.42081699e+10
1.78908166e+10 1.74929478e+10]
[ 5.25408000e+01 3.28790988e+10 2.74440000e+00 ... 3.88380258e+10
6.46539204e+09 6.00900728e+09]
[ 1.42203000e+01 5.91108572e+10 2.03830000e+00 ... 2.02066110e+11
4.50987171e+10 4.13284212e+10]]
形状
(2318, 7)
原来形状
(2318, 12)
3、皮尔逊相关系数(Pearson Correlation Coefficient)
反映变量之间相关关系密切程度的统计指标
相关系数的值介于–1与+1之间,即–1≤ r ≤+1。其性质如下
- 当r>0时,表示两变量正相关,r<0时,两变量为负相关
- 当|r|=1时,表示两变量为完全相关,当r=0时,表示两变量间无相关关系
- 当0<|r|<1时,表示两变量存在一定程度的相关。且|r|越接近1,两变量间线性关系越密切;|r|越接近于0,表示两变量的线性相关越弱
- 一般可按三级划分:|r|<0.4为低度相关;0.4≤|r|<0.7为显著性相关;0.7≤|r|<1为高度线性相关
API
from scipy.stats import pearsonr
from scipy.stats import pearsonr
import matplotlib.pyplot as plt
def pearsonr_demo():
"""
相关系数计算
:return: None
"""
data = pd.read_csv("factor_returns.csv")
factor = ['pe_ratio', 'pb_ratio', 'market_cap', 'return_on_asset_net_profit', 'du_return_on_equity', 'ev',
'earnings_per_share', 'revenue', 'total_expense']
for i in range(len(factor)):
for j in range(i, len(factor) - 1):
print(
"指标%s与指标%s之间的相关性大小为%f" % (factor[i], factor[j + 1], pearsonr(data[factor[i]], data[factor[j + 1]])[0]))
plt.figure(figsize=(20, 8), dpi=100)
plt.scatter(data['revenue'], data['total_expense'])
plt.show()
return None
if __name__ == "__main__":
# 代码11 计算皮尔逊相关系数
pearsonr_demo()
指标pe_ratio与指标pb_ratio之间的相关性大小为-0.004389
指标pe_ratio与指标market_cap之间的相关性大小为-0.068861
指标pe_ratio与指标return_on_asset_net_profit之间的相关性大小为-0.066009
指标pe_ratio与指标du_return_on_equity之间的相关性大小为-0.082364
指标pe_ratio与指标ev之间的相关性大小为-0.046159
指标pe_ratio与指标earnings_per_share之间的相关性大小为-0.072082
指标pe_ratio与指标revenue之间的相关性大小为-0.058693
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KDoPiIxN-1637326542945)(https://i.loli.net/2021/11/07/lTZ67OE9t1pka4u.png)]
5、主成分分析
1、介绍
- 定义:高维数据转化为低维数据的过程,在此过程中可能会舍弃原有数据、创造新的变量
- 作用:是数据维数压缩,尽可能降低原数据的维数(复杂度),损失少量信息。
- 应用:回归分析或者聚类分析当中
2、apl
from sklearn.decomposition import PCA
sklearn.decomposition.PCA(n_components=None)
- n_components:
- 小数:表示保留百分之多少的信息
- 整数:减少到多少特征
- PCA.fit_transform(X) X:numpy array格式的数据[n_samples,n_features]
- 返回值:转换后指定维度的array
from sklearn.decomposition import PCA
def PCA_demo():
"""
主成分分析降维
:return:
"""
# 1 导入数据
data = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
# 2 实例化
transfer = PCA(n_components=0.5)
# 3 调用fit_funcition函数
data_new = transfer.fit_transform(data)
print("data_new\n",data_new)
return None
if __name__ == "__main__":
# 代码12 PCA降维
PCA_demo()
保留90%的信息,降维结果为:
[[ -3.13587302e-16 3.82970843e+00]
[ -5.74456265e+00 -1.91485422e+00]
[ 5.74456265e+00 -1.91485422e+00]]
降维到3维的结果:
[[ -3.13587302e-16 3.82970843e+00 4.59544715e-16]
[ -5.74456265e+00 -1.91485422e+00 4.59544715e-16]
[ 5.74456265e+00 -1.91485422e+00 4.59544715e-16]]
三、分类算法
1、sklearn转换去和估计器
1、转换器
特征工程父类,所有的特征工程都会调用这个
- 实例化(Transformer)
- 调用fit_transform()方法
2、估计器(estimaor)
sklearn机器学习算法的实现
-
实例化一个estimateor
-
生成模型
estimator.fit(x_train,y_train)
- 评估模型好坏
-
法一、直接对比真实值与预测值
y_predict = estimato.predict(x_test)
t_test == y_predict
-
法二、计算准确率
accuracy = estimator.score(x_test,y_test)
-
2、KNN算法)(K近邻算法)
1、原理:根据邻居推算类别
分类时,对新的实例,根据其 k 个最近邻的训练实例的类别,通过多数表决等方式进行预测。k 值的选择,距离度量和分类决策规则是 k 近邻算法的三个基本要素
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Y1xPCPa0-1637326542946)(https://i.loli.net/2021/11/09/YebpDgyFwc7QzVW.png)]
2、距离度量
特征空间中两个实例点的距离时两个实例点相似程度的反映.
- 闵可夫斯基距离
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eVzT7f93-1637326542948)(https://i.loli.net/2021/11/09/YDIk3cf1psqnUyG.png)]
- p=无穷:表示距离坐标最大值
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-muxYwXx8-1637326542951)(https://i.loli.net/2021/11/09/8XT2ZRKJHwUFb9r.png)]
3、k值的选择
给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的k个实例,这k个实例的多数属于哪个类,就把该输入实例分为那个类
如果选择较小的 k 值,就相当于用较小的领域中的训练实例进行预测,只有与输入实例较近的的训练实例才会对预测结果起作用。但缺点是预测结果会对近邻的实例点非常敏感。这意味着整体模型变得更复杂,容易发生过拟合.
相反如果选择较大的 k 值,就相当于用较大领域中的训练实例进行预测. 这时与输入实例较远的训练实例也会对预测起作用,使预测发生错误。k 值的增大就意味着整体的模型变得简单。如果 k=N, 那么无论输入实例是什么,都将简单地预测它属于在训练实例中最多的类。这时,模型过于简单,完全忽略训练实例中的大量有用信息。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WAwQxWov-1637326542952)(https://i.loli.net/2021/11/09/OsIyqMTzC14nwxK.png)]
放入一个待分类的实例
• k = 1,按照某种距离度量找到最邻近的1个
训练样本测试实例的类别,判定为类1
• k = 3,按照某种距离度量找到最邻近的3个
训练样本测试实例的类别,判定为类2
• k = 5,按照某种距离度量找到最邻近的5个
训练样本测试实例的类别,判定为类1
4、KNN三要素
- K值选择
- 距离度量
- 分类决策规则(常采用投票规则)
5、APL
-
#第1步:从sklearn中导入模型 from sklearn.neighbors import KNeighborsClassifier sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm='auto') #第2步:创建模型的实例 knn=KNeighborsClassifier(n_neighbors=k,algorithm='auto') # n_neighbors:int,可选(默认= 5),k_neighbors查询默认使用的邻居数,k值。 #algorithm:{‘auto’,‘ball_tree’,‘kd_tree’,‘brute’},可选用于计算最近邻居的算法:‘ball_tree’将会使用 BallTree,‘kd_tree’将使用 KDTree。‘auto’将尝试根据传递给fit方法的值来决定最合适的算法。 (不同实现方式影响效率) #p 计算距离的方式p=2表示欧氏距离 #第3步:模型训练 knn.fit(X_train,y_train) #第4步:预测待分类数据的类别标签 y_pred=knn.predict(X_test)#第1步:从sklearn中导入模型 from sklearn.neighbors import KNeighborsRegressor # 第2步:创建模型的实例 knn = KNeighborsRegressor(n_neighbors=2 #第3步:模型训练 knn.fit(X_train,y_train) # 第4步:预测待分类数据的类别标签 y_pred=knn.predict(X_test)
6、案例一:鸢尾花
from sklearn.neighbors import KNeighborsClassifier#KNN算法
from sklearn.model_selection import train_test_split#数据划分
from sklearn.datasets import load_iris#鸢尾花数据集
from sklearn.preprocessing import StandardScaler#标准化
# 鸢尾花种类分类
def knn_iris():
"""
用KNN对鸢尾花种类分类
:return:
"""
# (1) 获取数据
iris = load_iris()
# (2)划分数据集
x_train,x_test,y_train,y_test = train_test_split(iris.data,iris.target,random_state=6)
# (3)特征工程:标准化
transfer = StandardScaler()
x_train= transfer.fit_transform(x_train)#训练集要标准化
x_test = transfer.fit_transform(x_test)#测试集也要标准化
# (4)KNN 算法预估器
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(x_train,y_train)
# (5)模型评估
# 法一:直接比对真实值和预测值
y_predict = knn.predict(x_test)
print("y_predice:\n",y_predict)
print("直接对比真实值和预测值:\n",y_test==y_predict)
# 法二:计算准确率
score = knn.score(x_test,y_test)
print("准确率为:\n",score)
return None
if __name__ == "__main__":
# 代码1 用KNN对鸢尾花尽心种类预测
knn_iris()
7、案例二、预测签到位置
import pandas as pd
import numpy as np
from sklearn.neighbors import KNeighborsClassifier #KNN
from sklearn.model_selection import train_test_split#数据集的划分
from sklearn.preprocessing import StandardScaler#标准化
from sklearn.model_selection import GridSearchCV#网格搜索
data = pd.read_csv("data/facebook-v-predicting-check-ins/train.csv")
#数据处理
# 缩小数据集范围
data = data.query("x > 1 & x < 1.25 & y > 2.5 & y < 2.75")
data
# 将时间转换为周、日、小时
# print(data["time"])
time_value = pd.to_datetime(data['time'],unit='s')#将时间戳转换成日期格式,时间戳单位是秒
# print(time_value)
time_value = pd.DatetimeIndex(time_value)#转为datetimeindex数据格式以便于后续处理
# print(time_value)
data['day'] = time_value.day
data['hour']=time_value.hour
data['weekday']= time_value.weekday
pritn(data.describe)
# 删除没用的日期数据
data = data.drop(['time'],axis = 1)
print(data)
# 将签到位置少于n个用户的删除
place_count = data.groupby("place_id").count()['row_id']#计算每一个地点签到的次数
print(place_count)
place_count[place_count>3].head() #筛选处签到次数大于3的id
#用data中的ID与筛选出来的id进行匹配,显示筛选出的行
data_final = data[data['place_id'].isin(place_count[place_count > 3 ].index.values)]
print(data_final)
# 筛选特征值和目标值
X = data_final[['x','y','accuracy','hour','day','weekday']]
y = data_final['place_id']
print(X.head())
print(y.head())
#数据集划分
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2)
# 标准化
transfer = StandardScaler()
X_train = transfer.fit_transform(X_train)
X_test = transfer.fit_transform(X_test)
# KNN算法预估器
estimator = KNeighborsClassifier()
# 网格搜索
param_dict = {"n_neighbors":[1,3,5,7,9]}
estimator = GridSearchCV(estimator,param_grid=param_dict,cv=3)
estimator.fit(X_train,y_train)
# 模型评估
# 方法1:
y_predict = estimator.predict(X_test)
print("真实值与预测值:\n",y_test == y_predict)
# 方法2:
score = estimator.score(X_test,y_test)
print("准确率:",score)
# 最佳参数
print("最佳参数:",estimator.best_params_)
print("最佳结果:",estimator.best_score_)
print("最佳估计器:",estimator.best_estimator_)
print("交叉验证结果:",estimator.cv_results_)
8、评价
- 优点:简单,易于理解,易于实现,无需训练
- 缺点:
- 懒惰算法,对测试样本分类时的计算量大,内存开销大
- 必须指定K值,K值选择不当则分类精度不能保证
- 使用场景:小数据场景,几千~几万样本,具体场景具体业务去测试
3、朴素贝叶斯算法(朴素即为相互独立+贝叶斯)
1、流程
- 找到特征值X={x1,x2,x3,…xm}(X={有星星,有云,有风…})
- 找到标签值y={y1,y2,…yn}(y={晴天、阴天})
- 分别计算后验概率p(y1|X)、p(y2|X)、p(y3|X)…p(yn|X)
- 如果p(yk|X)=max{p(y1|X),p(y2|X)…p(yn|X)}则yk为最终预测值
2、概念
-
完备事件组:把全集切分成几个子集,这几个子集互不相容、称这些子集为完备事件组
-
条件概率:后验概率,表示实验中各种"原因"可能发生的大小
P(A|B):在B发生条件下A发生的概率
-
相互独立:P(A,B )= P( A ) * P( B )
-
先验概率:在测试之前是已知的,一半来自过往的经验
-
全概率:
P ( A ) = ∑ n = 1 x P ( B i ) P ( A ∣ B i ) P(A) = \displaystyle \sum^x_{n=1}P(B_i)P(A|B_i) P(A)=n=1∑xP(Bi)P(A∣Bi)
把每一部分A的概率加起来其中 A概率为B的概率*B发生条件下A发生概率,B为完备事件组 -
贝叶斯公式
P ( B k ∣ A ) = P ( B k ∣ A ) P ( A ) = P ( B k ) P ( A ∣ B k ) ∑ i = 1 n P ( B i ) P ( A ∣ B i ) , k = 1 , 2 , 3... , n P(B_k|A)=\frac{P(B_k|A)}{P(A)}=\frac{P(B_k)P(A|B_k)}{\displaystyle \sum^n_{i=1}P(B_i)P(A|B_i)},k=1,2,3...,n P(Bk∣A)=P(A)P(Bk∣A)=i=1∑nP(Bi)P(A∣Bi)P(Bk)P(A∣Bk),k=1,2,3...,n -
朴素贝叶斯
假设特征与特征之间相互独立
3、例子
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nNnfyupd-1637326542953)(https://i.loli.net/2021/11/16/wuWBXarEzShAJH5.png)]
- 女神喜欢的概率
P = 4 / 7 P=4/7 P=4/7
职业是程序员并且女神喜欢的概率
P = 1 / 7 P=1/7 P=1/7
在女神喜欢的条件下,职业是程序员概率
P = 2 / 4 P =2/4 P=2/4
在女神喜欢条件下,职业是程序员 体重超重的概率是多少?
P = 1 / 4 P= 1/4 P=1/4
小明是产品经理,超重,问女神喜欢的概率是多少?
分子:P(产品经理,超重|喜欢) * P(喜欢)
分母:P(产品经理,超重)
p(程序员, 匀称) = P(程序员)P(匀称) =3/7*(4/7) = 12/49
P(产品, 超重|喜欢) = P(产品|喜欢)P(超重|喜欢)=1/2 * 1/4 = 1/8
4、拉普拉斯平滑系数
防止计算出的分类概率为0
P ( F 1 ∣ C ) = N i + α N + α m P(F_1|C)=\frac{N_i+\alpha}{N+{\alpha}m} P(F1∣C)=N+αmNi+α
α 表 示 为 指 定 系 数 , 一 般 为 1 , m 表 示 训 练 文 档 总 统 计 出 的 特 征 词 个 数 。 {\alpha}表示为指定系数,一般为1,m表示训练文档总统计出的特征词个数。 α表示为指定系数,一般为1,m表示训练文档总统计出的特征词个数。
5、apl
- sklearn.naive_bayes.MultinomialNB(alpha = 1.0)
- 朴素贝叶斯分类
- alpha:拉普拉斯平滑系数
6、代码
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer#文本特征提取
from sklearn.naive_bayes import MultinomialNB
def naive_bayes():
"""
朴素贝叶斯对新闻进行分类
:return:
"""
# 1获取数据
news = fetch_20newsgroups(data_home='data',subset="all")
# data_home:指定数据获取后下载到哪里
# subset:数据获取什么,默认获取train,想要获取所有数据要指定为all
# 2划分数据集
X_train,X_test,y_train,y_test = train_test_split(news.data,news.target,train_size=0.2,random_state=1)
# 3特征工程:文本特征抽取-tfidf
transfer = TfidfVectorizer()
X_train = transfer.fit_transform(X_train)
X_test = transfer.transform(X_test)
# 4朴素贝叶算法进行模型预估流程
estimator = MultinomialNB()
estimator.fit(X_train,y_train)
# 5模型评估
# 法一:直接比对真实值和预测值
y_predict = estimator.predict(X_test)
print("y_predice:\n", y_predict)
print("直接对比真实值和预测值:\n", y_test == y_predict)
# 法二:计算准确率
score = estimator.score(X_test, y_test)
print("准确率为:\n", score)
return
if __name__ == "__main__":
naive_bayes()
7、总结
- 优点:
- 朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
- 对缺失数据不太敏感,算法也比较简单,常用于文本分类。
- 分类准确度高,速度快
- 缺点:
- 由于使用了样本属性独立性的假设,所以如果特征属性有关联时其效果不好
4、决策树(找到最高效的决策顺序)
1、公式+原理
(1)信息熵
(2)信息增益(ID3)
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QH2xNR4k-1637326542955)(https://i.loli.net/2021/11/11/mDxhIle38PtZAky.png)]
信 息 增 益 = 信 息 熵 − 加 权 熵 信息增益 = 信息熵-加权熵 信息增益=信息熵−加权熵
(3)信息增益率(C4.5)
对信息增益的改进,防止模型对样本数目过多偏爱。其中的HA(D),对于样本集合D,将当前特征A作为随机变量(取值是特征A的各个特征值),求得的经验熵。
是在信息增益的基础之上乘上一个惩罚参数。特征个数较多时,惩罚参数较小;特征个数较少时,惩罚参数较大是在信息增益的基础之上乘上一个惩罚参数。特征个数较多时,惩罚参数较小;特征个数较少时,惩罚参数较大
(4)gini系数(CART–二叉树)
只有二叉树可以处理连续数据,多类数据需要先看成二叉树在进行下一步划分。
Gini指数越小表示集合中被选中的样本被分错的概率越小,也就是说集合的纯度越高,反之,集合越不纯。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JL9wr1LF-1637326542958)(https://i.loli.net/2021/11/11/845VT27DLhOtvIo.png)]
假设集合中有K个类别:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hnI2xTVE-1637326542960)(https://i.loli.net/2021/11/11/382xspqUOGn4bom.png)]
2、计算举例
已知四个特征,预测是否贷款给某人。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zRkS67iu-1637326542961)(https://i.loli.net/2021/11/16/H49oL627Dk5izGO.png)]
信息熵:
H ( 总 ) = ( 6 15 ∗ l o g 2 9 15 + 9 15 ∗ l o g 2 6 15 ) ≈ 0.971 H(总)=(\frac{6}{15}*log_2{\frac{9}{15}} + \frac{9}{15}*log_2{\frac{6}{15}})\approx0.971 H(总)=(156∗log2159+159∗log2156)≈0.971
信息增益:
g ( D , 年 龄 ) = H ( 总 ) − H ( D ∣ 年 龄 ) g(D,年龄)=H(总)-H(D|年龄) g(D,年龄)=H(总)−H(D∣年龄)
H ( D ∣ 年 龄 ) = 5 15 ∗ H ( 青 年 ) + 5 15 ∗ H ( 中 年 ) + 5 15 ∗ H ( 老 年 ) H(D|年龄)=\frac{5}{15}*H(青年)+\frac{5}{15}*H(中年)+\frac{5}{15}*H(老年) H(D∣年龄)=155∗H(青年)+155∗H(中年)+155∗H(老年)
H ( 青 年 ) = − ( 2 5 ∗ l o g 2 2 5 + 3 5 ∗ l o g 2 3 5 ) H(青年)= -(\frac{2}{5}*log_2\frac {2}{5} + \frac{3}{5}*log_2\frac{3}{5}) H(青年)=−(52∗log252+53∗log253)
H ( 中 年 ) = − ( 2 5 ∗ l o g 2 2 5 + 3 5 ∗ l o g 2 3 5 ) H(中年)= -(\frac{2}{5}*log_2\frac {2}{5} + \frac{3}{5}*log_2\frac{3}{5}) H(中年)=−(52∗log252+53∗log253)
H ( 老 年 ) = − ( 1 5 ∗ l o g 2 1 5 + 4 5 ∗ l o g 2 4 5 ) H(老年)= -(\frac{1}{5}*log_2\frac {1}{5} + \frac{4}{5}*log_2\frac{4}{5}) H(老年)=−(51∗log251+54∗log254)
| g(D, A1) | g(D, A2) | g(D, A3) max | g(D, A4) |
|---|---|---|---|
| 0.313 | 0.324 | 0.420 | 0.363 |
GINI:
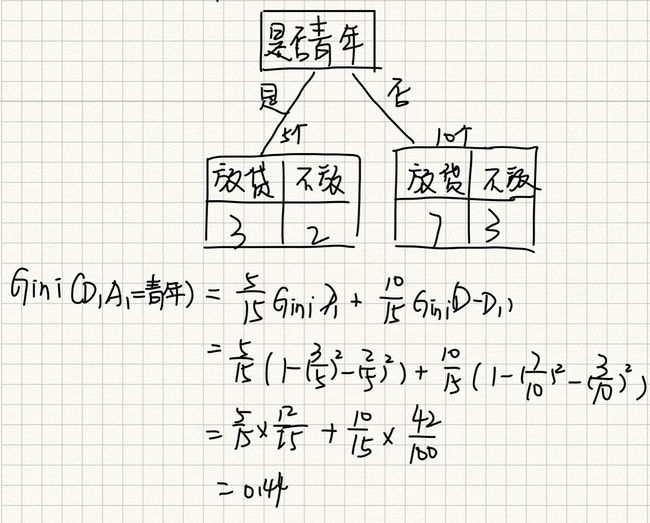
3、分类
-
ID3:信息增益 最大的准则
存在偏向于选择特征值较多的特征
-
C4.5:信息增益比 最大的准则
信息增益比偏向取值较少的特征
基于以上缺点,并不是直接选择信息增益率最大的特征,而是现在候选特征中找出信息增益高于平均水平的特征,然后在这些特征中再选择信息增益率最高的特征
-
CART
- 分类树: 基尼系数 最小的准则 在sklearn中可以选择划分的默认原则
- 优势:划分更加细致(从后面例子的树显示来理解)
4、APL
class sklearn.tree.DecisionTreeClassifier(criterion=’gini’, max_depth=None,random_state=None)
- 决策树分类器
- criterion:默认是’gini’系数,也可以选择信息增益的熵’entropy’
- max_depth:树的深度大小
- random_state:随机数种子
5、代码
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
def tree_demo():
"""
使用决策树对鸢尾花进行分类处理
:return:
"""
# 获取数据集
data = load_iris()
# 划分数据集
X_train,X_test,y_train,y_test = train_test_split(data.data,data.target,random_state=11,train_size=0.8)
# 决策树特征工程
estimator =DecisionTreeClassifier()
estimator.fit(X_train,y_train)
# 模型评估
y_pre = estimator.predict(X_test)
print("预测值",y_pre)
score = estimator.score(X_test,y_test)
print("准确率",score)
return None
if __name__ == "__main__":
tree_demo()
6、将树的结构导出
方式1:
import graphviz
import tree
dot_data = tree.export_graphviz(estimator, out_file=None,
class_names=["琴酒", '伏特加', '雪莉'], # 中文会出现乱码
filled=True, # 是否填充颜色
rounded=True, # 框的形状
special_characters=True)
graph = graphviz.Source(dot_data.replace('helvetica', '"Microsoft YaHei"'), encoding='utf-8')
graph.render('data/tree_iris') # 生成一个pdf到指定文件夹下
graph = pydotplus.graph_from_dot_data(dot_data)
Image(graph.create_png()) # 显示代码,pycharm显示不出来,jupyter可以
方式2:
from sklearn.tree import export_graphviz
tree.export_graphviz(estimator,out_file="data\iris_tree.dot")
#生成是一个dox文件,需要在网站上解析
7、泰坦尼克号
from sklearn.model_selection import train_test_split
from sklearn.tree import export_graphviz
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
import graphviz
import pandas as pd
##根据构建的决策树模型画出决策图像
# 这里需要安装pydotplus库以及graphviz这个软件,才能输出下面的图
# 可以参照:https://blog.csdn.net/qq_40304090/article/details/88594813
from sklearn import tree
import pydotplus
from IPython.display import Image
from sklearn.feature_extraction import DictVectorizer
def Titanic_mode():
"""
决策树处理泰坦尼克
:return:
"""
# 获取数据
data = pd.read_csv("data/titanic/train.csv")
print(data.head())
# 选择特征以及标签
x = data[['Pclass','Sex','Age']]
y = data['Survived']
# 数据处理
#缺失值
x['Age'].fillna(x['Age'].mean(),inplace=True)
#特征值转为字典类
dict = DictVectorizer(sparse=False)
x = dict.fit_transform(x.to_dict(orient='records'))
print(dict.get_feature_names())
# 划分数据集
X_train,X_test,y_train,y_test = train_test_split(x,y,random_state=11,train_size=0.8)
# 字典特征抽取
# 决策树
# 决策树特征工程
estimator = DecisionTreeClassifier()
estimator.fit(X_train, y_train)
# 模型评估
y_pre = estimator.predict(X_test)
print("预测值", y_pre)
score = estimator.score(X_test, y_test)
print("准确率", score)
# 可视化决策树
# 方式1
# tree.export_graphviz(estimator, out_file="data\iris_tree.dot")
# 方式2
dot_data = tree.export_graphviz(estimator, out_file=None,
# 中文会出现乱码
filled=True, # 是否填充颜色
rounded=True, # 框的形状
special_characters=True)
graph = graphviz.Source(dot_data.replace('helvetica', '"Microsoft YaHei"'), encoding='utf-8') # 中文乱码问题
graph.render('data/tree_Titanic') # 生成一个pdf到指定文件夹下
graph = pydotplus.graph_from_dot_data(dot_data)
Image(graph.create_png()) # 显示代码,pycharm显示不出来,jupyter可以
return None
if __name__ == "__main__":
# tree_demo()
Titanic_mode()
5、随机森林
1、集成学习方法
集成学习通过建立几个模型组合的来解决单一预测问题。它的工作原理是生成多个分类器/模型,各自独立地学习和作出预测。这些预测最后结合成组合预测,因此优于任何一个单分类的做出预测。
2、随机森林方法
- 训练集随机:随机有放回抽样,生成训练集
- 特征随机:从M个特征中随机抽取m个特征(M>>m)可以实现降维
- [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cD9oqZDK-1637326542962)(https://i.loli.net/2021/11/16/YbBzXsgVNAt7Dme.png)]
3、APL
-
class sklearn.ensemble.RandomForestClassifier(
n_estimators=10, criterion=’gini’, max_depth=None, bootstrap=True, random_state=None, min_samples_split=2)
- 随机森林分类器
- n_estimators:integer,optional(default = 10)森林里的树木数量120,200,300,500,800,1200
- criteria:string,可选(default =“gini”)分割特征的测量方法
- max_depth:integer或None,可选(默认=无)树的最大深度 5,8,15,25,30
- max_features="auto”,每个决策树的最大特征数量
- If “auto”, then
max_features=sqrt(n_features). - If “sqrt”, then
max_features=sqrt(n_features)(same as “auto”). - If “log2”, then
max_features=log2(n_features). - If None, then
max_features=n_features.
- If “auto”, then
- bootstrap:boolean,optional(default = True)是否在构建树时使用放回抽样
- min_samples_split:节点划分最少样本数
- min_samples_leaf:叶子节点的最小样本数
-
超参数:n_estimator, max_depth, min_samples_split,min_samples_leaf
4、鸢尾花评估
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
import pandas as pd
from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import GridSearchCV#网格搜索
def random_foreat():
"""
使用随机森林对泰坦尼克号进行预测
:return:
"""
data = pd.read_csv("data/titanic/train.csv")
print(data.head())
# 选择特征以及标签
x = data[['Pclass', 'Sex', 'Age']]
y = data['Survived']
# 数据处理
# 缺失值
x['Age'].fillna(x['Age'].mean(), inplace=True)
# 特征值转为字典类
dict = DictVectorizer(sparse=False)
x = dict.fit_transform(x.to_dict(orient='records'))
print(dict.get_feature_names())
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(x, y, random_state=11, train_size=0.8)
#随机森林模型训练
estimator = RandomForestClassifier()
# 网格搜索
param_dict = {"n_estimators": [120,200,300,500,800,1200], "max_depth": [5, 8, 15, 25, 30]}
estimator = GridSearchCV(estimator,param_grid=param_dict,cv=3)
estimator.fit(X_train,y_train)
y_pre = estimator.predict(X_test)
print("预测值", y_pre)
score = estimator.score(X_test, y_test)
print("准确率", score)
# 最佳参数
print("最佳参数:", estimator.best_params_)
print("最佳结果:", estimator.best_score_)
print("最佳估计器:", estimator.best_estimator_)
print("交叉验证结果:", estimator.cv_results_)
return None
if __name__ =="__main__":
random_foreat()
6、模型选择与评优
(1)交叉验证Cross Validation
交叉验证:此概念针对训练集,将拿到的训练数据,分为训练和验证集。以下图为例:将数据分成5份,其中一份作为验证集。然后经过5次(组)的测试,每次都更换不同的验证集。即得到5组模型的结果,取平均值作为最终结果。又称5折交叉验证。
将训练集训练好的模型利用test进行模型评估
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3PLQGsaY-1637326542963)(https://i.loli.net/2021/11/09/qYNWkmRE1XvzBAb.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VeUIuBw2-1637326542963)(https://i.loli.net/2021/11/09/WDPUo9phgRvkljB.png)]
(2)网格搜索Grid Search
每组超参数都采用交叉验证来进行评估。最后选出最优参数组合建立模型。
APL
sklearn.model_selection.GridSearchCV(knn, param_grid=None,cv=None)
-
knn:估计器对象(KNN实力化了的模型)
-
param_grid:估计器参数需要传入一个字典(dict){“n_neighbors”:[1,3,5]}
-
cv:指定几折交叉验证
-
fit:输入训练数据
-
score:准确率
结果分析:
-
print("最佳估计器: ",knn.best_estimator_) print("最好结果 ",knn.best_score_) print("每次交叉验证之后的准确率: ",knn.cv_results_) print("最佳k: ", knn.best_params_)
from sklearn.neighbors import KNeighborsClassifier#KNN算法
from sklearn.model_selection import train_test_split#数据划分
from sklearn.datasets import load_iris#鸢尾花数据集
from sklearn.preprocessing import StandardScaler#标准化
from sklearn.model_selection import GridSearchCV
def Titanic_mode():
"""
决策树处理泰坦尼克
:return:
"""
# 获取数据
data = pd.read_csv("data/titanic/train.csv")
print(data.head())
# 选择特征以及标签
x = data[['Pclass','Sex','Age']]
y = data['Survived']
# 数据处理
#缺失值
x['Age'].fillna(x['Age'].mean(),inplace=True)
#特征值转为字典类
dict = DictVectorizer(sparse=False)
x = dict.fit_transform(x.to_dict(orient='records'))
print(dict.get_feature_names())
# 划分数据集
X_train,X_test,y_train,y_test = train_test_split(x,y,random_state=11,train_size=0.8)
# 字典特征抽取
# 决策树
# 决策树特征工程
estimator = DecisionTreeClassifier()
estimator.fit(X_train, y_train)
# 模型评估
y_pre = estimator.predict(X_test)
print("预测值", y_pre)
score = estimator.score(X_test, y_test)
print("准确率", score)
# 可视化决策树
# 方式1
# tree.export_graphviz(estimator, out_file="data\iris_tree.dot")
# 方式2
dot_data = tree.export_graphviz(estimator, out_file=None,
# 中文会出现乱码
filled=True, # 是否填充颜色
rounded=True, # 框的形状
special_characters=True)
graph = graphviz.Source(dot_data.replace('helvetica', '"Microsoft YaHei"'), encoding='utf-8') # 中文乱码问题
graph.render('data/tree_Titanic') # 生成一个pdf到指定文件夹下
graph = pydotplus.graph_from_dot_data(dot_data)
Image(graph.create_png()) # 显示代码,pycharm显示不出来,jupyter可以
return None
if __name__ == "__main__":
# 代码2 使用网格搜索找k值KNN鸢尾花进行分类
Grid_KNN_iris()
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7jEkCJLi-1637326542964)(https://i.loli.net/2021/11/09/6y8UvBS2Nj4udkm.png)]
四、回归问题
1、线性回归
1、原理
线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式。
自变量是一次称为单变量回归,大于一个自变量情况的叫做多元回归。
2、线性回归性能评估
法一:最小二乘
J ( θ ) = ( h w ( x 1 ) − y 1 ) 2 + ( h w ( x 2 ) − y 2 ) 2 + . . . + ( h w ( x m ) − y m ) 2 J(\theta)=(h_w(x_1)-y_1)^2+(h_w(x_2)-y_2)^2+...+(h_w(x_m)-y_m)^2 J(θ)=(hw(x1)−y1)2+(hw(x2)−y2)2+...+(hw(xm)−ym)2
- y_i为第i个训练样本的真实值
- h(x_i)为第i个训练样本特征值组合预测函数
- 又称最小二乘法
法二:均方误差
M S E = 1 m ∑ i = 1 m ( y i − y ˉ ) 2 MSE = \frac{1}{m}\displaystyle \sum_{i=1}^m(y^i-\bar{y})^2 MSE=m1i=1∑m(yi−yˉ)2
注:y^i为预测值,¯y为真实值
- sklearn.metrics.mean_squared_error(y_true, y_pred)
- 均方误差回归损失
- y_true:真实值
- y_pred:预测值
- return:浮点数结果
3、优化
方法一:梯度下降
w 1 = w 1 − α ∂ c o n t ( w 0 + w 1 x 1 ) ∂ w 1 w_1 = w_1-{\alpha}\frac{∂cont(w_0+w_1x_1)}{∂w_1} w1=w1−α∂w1∂cont(w0+w1x1)
w 0 = w 0 − α ∂ c o n t ( w 0 + w 1 x 1 ) ∂ w 1 w_0 = w_0-{\alpha}\frac{∂cont(w_0+w_1x_1)}{∂w_1} w0=w0−α∂w1∂cont(w0+w1x1)
α为学习速率,需要手动指定(超参数),α旁边的整体表示方向
沿着这个函数下降的方向找,最后就能找到山谷的最低点,然后更新W值
使用:面对训练数据规模十分庞大的任务 ,能够找到较好的结果
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-q4ykhlKx-1637326542965)(C:\Users\lenovo\AppData\Roaming\Typora\typora-user-images\image-20211117215140410.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-s8cafRId-1637326542965)(C:\Users\lenovo\AppData\Roaming\Typora\typora-user-images\image-20211117215152125.png)]
方法二:正规方程
w = ( X T X ) − 1 X T y w=(X^TX)^{-1}X^Ty w=(XTX)−1XTy
X为特征值矩阵,y为目标值矩阵。直接求到最好的结果
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-28OARJxj-1637326542966)(https://i.loli.net/2021/11/16/dz1vJrx9TcVisXy.gif)]
3、APL
-
sklearn.linear_model.LinearRegression(fit_intercept=True)
- 通过正规方程优化
- fit_intercept:是否计算偏置
- LinearRegression.coef_:回归系数
- LinearRegression.intercept_:偏置
-
sklearn.linear_model.SGDRegressor(loss=“squared_loss”, fit_intercept=True, learning_rate =‘invscaling’, eta0=0.01)
- SGDRegressor类实现了随机梯度下降学习,它支持不同的loss函数和正则化惩罚项来拟合线性回归模型。
- loss:损失类型
- loss=”squared_loss”: 普通最小二乘法
- fit_intercept:是否计算偏置
- learning_rate : string, optional
- 学习率填充
- ’constant’: eta = eta0
- ’optimal’: eta = 1.0 / (alpha * (t + t0)) [default]
- ‘invscaling’: eta = eta0 / pow(t, power_t)
- power_t=0.25:存在父类当中
- 对于一个常数值的学习率来说,可以使用learning_rate=’constant’ ,并使用eta0来指定学习率。
- SGDRegressor.coef_:回归系数
- SGDRegressor.intercept_:偏置
4、代码
使用正规方程+梯度下降对波士顿房价进行预测
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression#正规方程
from sklearn.linear_model import SGDRegressor#题梯度下降
from sklearn.metrics import mean_squared_error#均方误差
def liner_1():
"""
正规方程预测房屋价格
:return:
"""
# 1.数据获取
boston = load_boston()
# 2.划分数据集
x_train , x_test , y_train, y_test = train_test_split(boston.data , boston.target , random_state=22)
# 3.标准化
transfer = StandardScaler()
x_train= transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4.预估器
estimator = LinearRegression()
estimator.fit(x_train,y_train)
# 5.得出模型
print("正规方程的权重系数,\n",estimator.coef_)
print("正规方程偏置:\n",estimator.intercept_)
# 6.模型评估
y_pre = estimator.predict(x_test)
print("房价预测:\n",y_pre)
erro = mean_squared_error(y_test,y_pre)
print("正规方程均方误差:\n",erro)
return None
def liner_2():
"""
梯度下降预测房屋价格
:return:
"""
# 1.数据获取
boston = load_boston()
# 2.划分数据集
x_train , x_test , y_train , y_test = train_test_split(boston.data , boston.target , random_state=22)
# 3.标准化
transfer = StandardScaler()
x_train= transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4.预估器
estimator =SGDRegressor(learning_rate='constant',#选择学习率
eta0=0.001,
max_iter=10000#设置迭代次数
)
estimator.fit(x_train,y_train)
# 5.得出模型
print("梯度下降的权重系数,\n",estimator.coef_)
print("梯度下降偏置:\n",estimator.intercept_)
# 6.模型评估
y_pre = estimator.predict(x_test)
print("房价预测:\n",y_pre)
erro = mean_squared_error(y_test,y_pre)
print("梯度下降均方误差:\n",erro)
return None
if __name__=="__main__":
liner_1()
liner_2()
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率 | 不需要 |
| 需要迭代求解 | 一次运算得出 |
| 特征数量较大可以使用 | 需要计算方程,时间复杂度高O(n3) |
- 线性回归的损失函数-均方误差
- 线性回归的优化方法
- 正规方程
- 梯度下降
- 线性回归的性能衡量方法-均方误差
- sklearn的SGDRegressor API 参数
2、过拟合与欠拟合
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5eMYWYHY-1637326542967)(https://i.loli.net/2021/11/18/s3ozfjTJNAa951V.png)]
1、过拟合问题解决方法
- L2正则化
- 作用:可以使得其中一些W的都很小,都接近于0,削弱某个特征的影响
- 优点:越小的参数说明模型越简单,越简单的模型则越不容易产生过拟合现象
- Ridge回归(岭回归)
- L1正则化
- 作用:可以使得其中一些W的值直接为0,删除这个特征的影响
- LASSO回归
2、岭回归
- sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver=“auto”, normalize=False)
- 具有l2正则化的线性回归
- alpha:正则化力度(惩罚项系数),也叫 λ
- λ取值:0~1 1~10
- fit_intercept:是否添加偏置,True添加后更准确
- solver:会根据数据自动选择优化方法
- sag:如果数据集、特征都比较大,选择该随机梯度下降优化
- normalize:数据是否进行标准化
- normalize=False:可以在fit之前调用
- normalize=True 不用做标准化了
- preprocessing.StandardScaler标准化数据
- Ridge.coef_:回归权重
- Ridge.intercept_:回归偏置
Ridge方法相当于SGDRegressor(penalty=‘l2’, loss=“squared_loss”)
只不过SGDRegressor实现了一个普通的随机梯度下降学习,推荐使用Ridge(实现了SAG高级梯度下降)
def liner_3():
"""
岭回归 预测房屋价格
:return:
"""
# 1.数据获取
boston = load_boston()
# 2.划分数据集
x_train , x_test , y_train, y_test = train_test_split(boston.data , boston.target , random_state=22)
# 3.标准化
transfer = StandardScaler()
x_train= transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4.预估器
estimator = Ridge()
estimator.fit(x_train,y_train)
# 5.得出模型
print("岭回归权重系数,\n",estimator.coef_)
print("岭回归偏置:\n",estimator.intercept_)
# 6.模型评估
y_pre = estimator.predict(x_test)
print("房价预测:\n",y_pre)
erro = mean_squared_error(y_test,y_pre)
print("岭回归均方误差:\n",erro)
return None
if __name__=="__main__":
# 岭回归
liner_3()
3、逻辑回归
1、了解逻辑回归
- 解决二分类问题的利器
- 线性回归的输出就是逻辑回归的输入
- 带入sigmoid函数中,输出结果【0,1】之间的概率值,默认0.5为阈值
2、sigmoid函数
g ( θ T x ) = 1 1 + e θ T x g(\theta^Tx)=\frac{1}{1+e^{\theta^Tx}} g(θTx)=1+eθTx1
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZBDr5VfJ-1637326542967)(https://i.loli.net/2021/11/18/ULjV1YdSfryGlBK.png)]
推导过程:
Logistic 回归模型是建立p/(1-p)与自变量之间关系的线性回归模型。用数学语言来表示,可以表达为:
l n p 1 − p = β 0 + β 1 x 1 + β 2 x 2 + . . . + β p x p + ϵ ln\frac{p}{1-p}=\beta_0+\beta_1x_1+\beta_2x_2+...+\beta_px_p+\epsilon ln1−pp=β0+β1x1+β2x2+...+βpxp+ϵ
记 g ( x ) = β 0 + β 1 x 1 + β 2 x 2 + . . . + β p x p + ϵ , 得 到 记g(x) =\beta_0+\beta_1x_1+\beta_2x_2+...+\beta_px_p+\epsilon,得到 记g(x)=β0+β1x1+β2x2+...+βpxp+ϵ,得到
p = P ( y = 1 ∣ X ) = 1 1 + e − g ( x ) p = P(y=1|X)=\frac{1}{1+e^{-g(x)}} p=P(y=1∣X)=1+e−g(x)1
p = P ( y = 0 ∣ X ) = 1 1 + e g ( x ) p = P(y=0|X)=\frac{1}{1+e^{g(x)}} p=P(y=0∣X)=1+eg(x)1
3、建模步骤
1、**分析模型:**根据分析目的设置指标变量(因变量与自变量),然后收集数据。
2、**模型估计:*y 取 1 的概率是 p = P(y = 1|*X), 取 0 的概率是 1 -p。用 ln (p/(1-p))和自变量列出线性回归方程,估计出模型中的回归系数。
3、**进行回归系数的显著性检验:**在多元线性回归中,回归方程显著并不意味着每个自变量对 y 的影响都是显著的,为了从回归方程中剔除那些次要的、可有可无的变量,重新建立更为简单有效的回归方程,需要对每个自变量进行显著性检验,检验结果由参数估计表得到。或采用逐步回归法,首先剔除掉最不显著的自变量,重新构造回归方程,一直到模型和参与的回归系数都通过检验。
4、**模型应用:**输入自变量的取值,就可以得到预测变量的值,或者根据预测变量的值取控
制自变量的取值
4、逻辑函数的损失
对数似然损失
C O S T ( h θ ( x ) , y ) = ∑ i = 1 m − y i l o g ( h θ ( x ) ) − ( 1 − y i ) l o g ( 1 − h θ ( x ) ) COST(h_\theta(x),y) = \sum^m_{i=1}-y_ilog(h_\theta(x))-(1-y_i)log(1-h_\theta(x)) COST(hθ(x),y)=i=1∑m−yilog(hθ(x))−(1−yi)log(1−hθ(x))
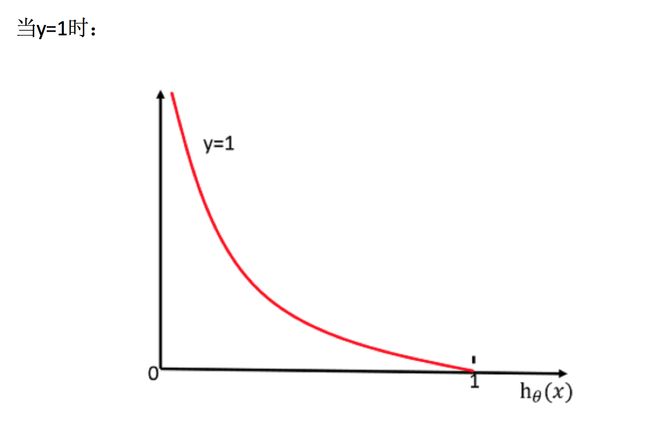
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Kk857HGD-1637326542968)(E:/机器学习/机器学习资料(黑马)/机器学习3天HTML/images/损失计算过程.png)]
5、APL
- sklearn.linear_model.LogisticRegression(solver=‘liblinear’, penalty=‘l2’, C = 1.0)
- solver:优化求解方式(默认开源的liblinear库实现,内部使用了坐标轴下降法来迭代优化损失函数)
- sag:根据数据集自动选择,随机平均梯度下降
- penalty:正则化的种类
- C:正则化力度
- solver:优化求解方式(默认开源的liblinear库实现,内部使用了坐标轴下降法来迭代优化损失函数)
LogisticRegression方法相当于 SGDClassifier(loss=“log”, penalty=" ")
SGDClassifier实现了一个普通的随机梯度下降学习,也支持平均随机梯度下降法(ASGD),可以通过设置average=True。而使用LogisticRegression(实现了SAG)
6、肿瘤性质判断案例
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
import numpy as np
import pandas as pd
def logistic_demo():
"""
通过逻辑回归对肿瘤性质进行预测
:return:
"""
# 获取数据(读取时加上names)
cloumn_names = ['Sample code number','Clump Thickness','Uniformity of Cell Size','Uniformity of Cell Shape','Marginal Adhesion',
'Single Epithelial Cell Size','Bare Nuclei','Bland Chromatin','Normal Nucleoli','Mitoses','Class']
data = pd.read_csv("data/cancer/breast-cancer-wisconsin.data",names = cloumn_names)
# 数据处理(缺失值处理)
# 替换为np.nan
data = data.replace(to_replace='?',value=np.nan)
# 删除nan所在的行
data.dropna(inplace = True)
# 查看是否有缺失值
# print(data.isnull().any())
# 数据集划分
x = data.iloc[:,1:-1]
y = data.Class
X_train,X_test,y_train,y_test = train_test_split(x,y,random_state=11,train_size=0.7)
# 特征工程(无量纲)
transfer = StandardScaler()
X_train = transfer.fit_transform(X_train)
X_test = transfer.transform(X_test)
# 逻辑回归模型
estimator = LogisticRegression()
estimator.fit(X_train,y_train)
# 查看模型偏置
print("回归系数",estimator.coef_)
print("偏置",estimator.intercept_)
# 模型评估
y_pre = estimator.predict(X_test)
print("预测类别:\n",y_pre,y_test)
score = estimator.score(X_test,y_test)
print("准确率\n",score)
return None
if __name__=="__main__":
# 逻辑回归模型
logistic_demo()
4、精确率与召回率
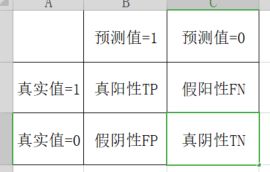
1、混淆矩阵
-
准确率:预测值与真实值相符合的概率
T P + T N T P + F X + F P + T V \frac{TP+TN}{TP+FX+FP+TV} TP+FX+FP+TVTP+TN -
precision精确率:预测结果为真中,真实为正真的比例
T P T P + F P \frac{TP}{TP+FP} TP+FPTP -
recall召回率:真实为真的样本中预测结果为真的比例(查的全,对正样本的区分能力)
T P T P + F N \frac{TP}{TP+FN} TP+FNTP
- F!-score :反映了模型的稳健型
F 1 = 2 T P 2 T P + F N + F P = 2 ∗ P r e c i s i o n ∗ R e c a l l P r e c i s i o n + R e c a l l F1 = \frac{2TP}{2TP+FN+FP}=\frac{2*Precision*Recall}{Precision+Recall} F1=2TP+FN+FP2TP=Precision+Recall2∗Precision∗Recall
2、APL
sklearn.metrics.classification_report(y_true, y_pred, labels=[], target_names=None )
- y_true:真实目标值
- y_pred:估计器预测目标值
- labels:指定类别对应的数字,传类别是传的数字
- target_names:目标类别名称(要把类别的数字对应到具体的名字)
- return:每个类别精确率与召回率
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5HWN2OA0-1637326542970)(https://i.loli.net/2021/11/19/dbm65kYQuwrayBl.png)]
3、ROC曲线+AUC指标
(1)应用
样本不均衡:样本正例反例数量差别过大
(2)原理
AUC 是ROC曲线与x围成的面积,越接近1越好,接近0.5越不好
- TPR = TP / (TP + FN)
- 所有真实类别为1的样本中,预测类别为1的比例
- FPR = FP / (FP + TN)
- 所有真实类别为0的样本中,预测类别为1的比例
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KjgFxHTi-1637326542970)(https://i.loli.net/2021/11/19/GnpiXmdNsbjHqWT.png)]
-
ROC曲线的横轴就是FPRate,纵轴就是TPRate,当二者相等时,表示的意义则是:对于不论真实类别是1还是0的样本,分类器预测为1的概率是相等的,此时AUC为0.5
(总共就两类,随便猜正确率最低为都猜同一种结果,效果最差为0.5,为了不让模型敷衍,有了AUC)
(3)APL
sklearn.metrics.roc_auc_score(y_true, y_pre)
- 计算ROC曲线面积,即AUC值
- y_true:每个样本的真实类别,必须为0(反例),1(正例)标记
- y_pre:每个样本预测的概率值
(4)ROC总结
- AUC只能用来评价二分类
- AUC非常适合评价样本不平衡中的分类器性能
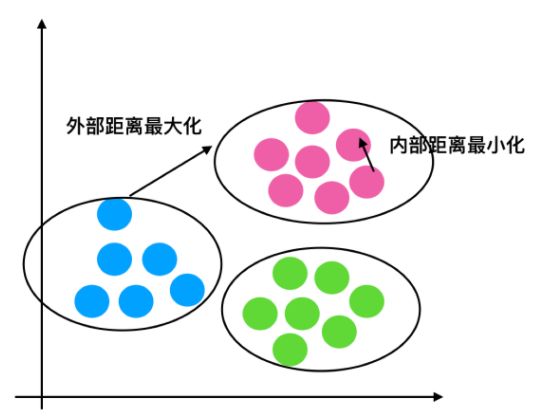
5、K_means
处理没有标签的数据,进行聚类。属于无监督学习算法算法
1、原理
-
1、随机设置K个特征空间内的点作为初始的聚类中心(也可以手动设置)
-
2、对于其他每个点计算到K个中心的距离,未知的点选择最近的一个聚类中心点作为标记类别
-
3、接着对着标记的聚类中心之后,重新计算出每个聚类的新中心点(平均值)
-
4、如果计算得出的新中心点与原中心点一样(或者达到设置的计算次数),那么结束
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pZ0NVmkb-1637326542971)(https://i.loli.net/2021/11/19/NDbwrQmHi8M53hV.png)]
中心点计算方法:
| A(a1,b1,c1) |
|---|
| B (a2,b2,c2) |
| … … … … |
| Z(a26,b26,c26) |
| 中心点 = (a平均,b平均,c平均) |
2、k值选择方法
-
每次聚类完成后计算每个点到其所属的簇中心的距离的平方和,此平方和是会逐渐变小的,直到 = 时,平方和为0,因为每个点都是它所在的簇中心本身。但是在这个平方和变化过程中,会出现一个拐点也即“肘”,根据拐点确定K值。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Ni7bt7JO-1637326542972)(https://i.loli.net/2021/11/19/vyF8unIap4iZtxQ.png)]
3、APL
- sklearn.cluster.KMeans(n_clusters=8,init=‘k-means++’)
- k-means聚类
- n_clusters:开始的聚类中心数量(也就是K值)
- init:初始化方法,默认为’k-means ++’
- labels_:默认标记的类型,可以和真实值比较(不是值比较)
4、对Instacart Market用户进行聚类
from sklearn.cluster import KMeans
import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import silhouette_score#轮廓系数
def kmeans_demo():
"""
使用kmeans对用户种类进行预测
:return:
"""
# 导数据
cloumn_names = ['Sample code number', 'Clump Thickness', 'Uniformity of Cell Size', 'Uniformity of Cell Shape',
'Marginal Adhesion',
'Single Epithelial Cell Size', 'Bare Nuclei', 'Bland Chromatin', 'Normal Nucleoli', 'Mitoses',
'Class']
data = pd.read_csv("data/cancer/breast-cancer-wisconsin.data", names=cloumn_names)
# 数据处理(缺失值处理)
# 替换为np.nan
data = data.replace(to_replace='?', value=np.nan)
# 删除nan所在的行
data.dropna(inplace=True)
# 查看是否有缺失值
# print(data.isnull().any())
data_new = data.iloc[:,:-1]
# 特征工程(无量纲)
transfer = StandardScaler()
data_new = transfer.fit_transform(data_new)
# kmeans模型进行训练
estimator = KMeans(n_clusters=3)
estimator.fit(data_new)#只需要传入特征值
pre = estimator.predict(data_new)
print(pre[:300])
# 对模型训练结果进行评估--轮廓系数
score = silhouette_score(data_new,pre)
print("轮廓系数:\n",score)
return None
if __name__=="__main__":
kmeans_demo()
5、轮廓系数
S C i = b i − a i m a x ( b i , a i ) SC_i= \frac{b_i-a_i}{max(b_i,a_i)} SCi=max(bi,ai)bi−ai
注 : 对 于 每 个 点 i 为 已 聚 类 数 据 中 的 样 本 , b i 为 i 到 其 它 族 群 的 所 有 样 本 的 距 离 最 小 值 , a i 为 i 到 本 身 簇 的 距 离 平 均 值 。 最 终 计 算 出 所 有 的 样 本 点 的 轮 廓 系 数 平 均 值 注:对于每个点i 为已聚类数据中的样本 ,b_i 为i 到其它族群的所有样本的距离最小值,a_i 为i 到本身簇的距离平均值。最终计算出所有的样本点的轮廓系数平均值 注:对于每个点i为已聚类数据中的样本,bi为i到其它族群的所有样本的距离最小值,ai为i到本身簇的距离平均值。最终计算出所有的样本点的轮廓系数平均值
如 果 b i > > a i : 趋 近 于 1 效 果 越 好 , b i < < a i : 趋 近 于 − 1 , 效 果 不 好 。 轮 廓 系 数 的 值 是 介 于 [ − 1 , 1 ] , 越 趋 近 于 1 代 表 内 聚 度 和 分 离 度 都 相 对 较 优 。 如果b_i>>a_i:趋近于1效果越好, b_i<
6、K-means总结
- 特点分析:采用迭代式算法,直观易懂并且非常实用
- 缺点:容易收敛到局部最优解(多次聚类)
6、模型保存与加载
(1)APL
-
import joblib
-
保存:joblib.dump(rf, ‘test.pkl’)
-
加载:estimator = joblib.load(‘test.pkl’)
# 保存模型 joblib.dump(estimator,"my.pkl")[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-H2ipy9ct-1637326542975)(https://i.loli.net/2021/11/19/WFeOLAlRgrdxQjG.png)]
# 加载模型 estimator = joblib.load("my.pkl")
-
Means(n_clusters=8,init=‘k-means++’)
- k-means聚类
- n_clusters:开始的聚类中心数量(也就是K值)
- init:初始化方法,默认为’k-means ++’
- labels_:默认标记的类型,可以和真实值比较(不是值比较)
4、对Instacart Market用户进行聚类
from sklearn.cluster import KMeans
import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import silhouette_score#轮廓系数
def kmeans_demo():
"""
使用kmeans对用户种类进行预测
:return:
"""
# 导数据
cloumn_names = ['Sample code number', 'Clump Thickness', 'Uniformity of Cell Size', 'Uniformity of Cell Shape',
'Marginal Adhesion',
'Single Epithelial Cell Size', 'Bare Nuclei', 'Bland Chromatin', 'Normal Nucleoli', 'Mitoses',
'Class']
data = pd.read_csv("data/cancer/breast-cancer-wisconsin.data", names=cloumn_names)
# 数据处理(缺失值处理)
# 替换为np.nan
data = data.replace(to_replace='?', value=np.nan)
# 删除nan所在的行
data.dropna(inplace=True)
# 查看是否有缺失值
# print(data.isnull().any())
data_new = data.iloc[:,:-1]
# 特征工程(无量纲)
transfer = StandardScaler()
data_new = transfer.fit_transform(data_new)
# kmeans模型进行训练
estimator = KMeans(n_clusters=3)
estimator.fit(data_new)#只需要传入特征值
pre = estimator.predict(data_new)
print(pre[:300])
# 对模型训练结果进行评估--轮廓系数
score = silhouette_score(data_new,pre)
print("轮廓系数:\n",score)
return None
if __name__=="__main__":
kmeans_demo()
5、轮廓系数
S C i = b i − a i m a x ( b i , a i ) SC_i= \frac{b_i-a_i}{max(b_i,a_i)} SCi=max(bi,ai)bi−ai
注 : 对 于 每 个 点 i 为 已 聚 类 数 据 中 的 样 本 , b i 为 i 到 其 它 族 群 的 所 有 样 本 的 距 离 最 小 值 , a i 为 i 到 本 身 簇 的 距 离 平 均 值 。 最 终 计 算 出 所 有 的 样 本 点 的 轮 廓 系 数 平 均 值 注:对于每个点i 为已聚类数据中的样本 ,b_i 为i 到其它族群的所有样本的距离最小值,a_i 为i 到本身簇的距离平均值。最终计算出所有的样本点的轮廓系数平均值 注:对于每个点i为已聚类数据中的样本,bi为i到其它族群的所有样本的距离最小值,ai为i到本身簇的距离平均值。最终计算出所有的样本点的轮廓系数平均值
如 果 b i > > a i : 趋 近 于 1 效 果 越 好 , b i < < a i : 趋 近 于 − 1 , 效 果 不 好 。 轮 廓 系 数 的 值 是 介 于 [ − 1 , 1 ] , 越 趋 近 于 1 代 表 内 聚 度 和 分 离 度 都 相 对 较 优 。 如果b_i>>a_i:趋近于1效果越好, b_i<
[外链图片转存中…(img-M80QbmPp-1637326542973)]
6、K-means总结
- 特点分析:采用迭代式算法,直观易懂并且非常实用
- 缺点:容易收敛到局部最优解(多次聚类)
6、模型保存与加载
(1)APL
-
import joblib
-
保存:joblib.dump(rf, ‘test.pkl’)
-
加载:estimator = joblib.load(‘test.pkl’)
# 保存模型 joblib.dump(estimator,"my.pkl")[外链图片转存中…(img-H2ipy9ct-1637326542975)]
# 加载模型 estimator = joblib.load("my.pkl")
-