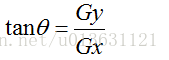白话文讲计算机视觉-第五讲-canny边缘检测算法

大家好，好快哦，今天是第五讲了，现在的时间是2018年5月27日，很快5月份就结束了，也就是说半年的时间就过去了，我过年的事儿还能记住呢。曾经有一个姓张的同学说过，时间随着年龄的增长会越来越快。以1岁时候过一年的时间来说，要是20岁就只有二十分之一的长度了。速度快了20倍。这个理论很有意思。我这个快30岁的人，时间确实过的飞快啊。

先说一下上节课的问题，上节课在开闭运算的时候有一个第八个参数叫做：morphologyDefaultBorderValue() ，这个参数是判断你是腐蚀还是膨胀，之前我们定义了超出边缘的话，我们假定为一个常数值。如果是膨胀的话那么边缘的常数值就是低亮（全0），如果是腐蚀的话就是高亮（全1）。它会返回一个64位的浮点数值（全0或者全1），之后根据我们图像的颜色深度，我们再改回32、16或者8位。

今天我要讲的内容是canny边缘检测。首先先说件事儿，我们的公众平台已经这么多人关注了，你们只看不转可不道义哦，你们学会了知识，在知网发表了几篇文，拿到了奖学金，我不需要你们的感谢，你们转发几条到朋友圈帮我宣传一下总可以吧？这里也给各位抱拳了。这也是为了更多中国人民能够学习到知识，把知识普及。促进我国的发展做贡献了！

废话就不说了，说一下canny吧，先说一下什么叫canny检测，canny是一个人，澳大利亚的人，这个人是一个天才，它发明了一种方法，能够把图片中的轮廓从图片中剥离出去。那么canny检测就很好理解了，检测啥？当然是检测图像的轮廓边缘啊。所以canny检测又称为边缘检测算法。那么这个算法是怎么进行计算的呢？其实它分为了5部分:

高斯滤波

首先第一部分是高斯滤波。我们在第三讲中说过了，滤波分为高通和低通滤波，低通滤波是进行去噪声用的。而计算方式是用一张图片与低通滤波器进行卷积。之前我们自己创造了一个滤波器：

这个是5*5的一个滤波器，所有的元素之和为1，这样的滤波器就是低通滤波器。然而我们一般不需要自己创造一个滤波器，而是用其它人创造好的东西，直接拿来用，这样的效果也比自己创造的好。于是我们就引入了高斯滤波器，他也是低通滤波器的一种。

那么高斯滤波器是什么样子的呢？其实就是基于高斯分布的滤波器，高斯分布也叫正态分布，X、Y两个变量的正态分布计算公式如下：

一般来说，在canny算法中是一个3*3的滤波器（必须是奇数），所以我们假定卷积核是一个3*3的矩阵，中心点的坐标是(2,2)，那么我们可以定义卷积核内每一个小矩形格的坐标：

(1,1)	(1,2)	(1,3)
(2,1)	(2,2)	(2,3)
(3,1)	(3,2)	(3,3)

那么这个矩阵里面对应正态分布计算公式的u1，u2，σ1，σ2怎么计算呢，我们先说一下u1,u2，这个说白了就是中心的位置，一维的正态分布就是中心点的坐标哦！二维同样也是的哦！那么中心点的位置是哪里呢？不用多说，当然是中央啦，也就是第二行第二列，所以u1=2,u2=2，如果它不是一个3*3的，比如5*5的卷积核，也就是2*2+1,2*2+1的卷积核，我们的u1=u2=2+1=3也就是第三行第三列。我们把2*2+1,2*2+1扩展一下，变成(2k+1)*(2k+1)的卷积核，那么它的u1=k+1，u2=k+1。

说完了u1,u2，我们再说一下σ1，σ2，我们假定的是这两个值是相等的，都等于：

σ= 0.3*((ksize-1)*0.5 - 1) + 0.8，比如我们是3*3的核，那么σ1，σ2就都为0.8。

这样我们的参数都确定好了，那么我们把卷积核内的坐标都带入进去，不就能把每一个小格子里面的H给就出来了么？求出的结果如下：

 

之后，我们要进行归一化处理，怎么归一化？这里和标准归一化有点区别。这里首先是用第一行第一列的数据的倒数除以里面的每一个数据，得到：

 

最后，我们保留整数位，舍弃小数位得到：

 

这样一个3*3的高斯卷积核就制作完毕了。

但是我们在canny里面用的高斯卷积和正常的卷积核还是有一些出路，出路就在我们归一化的时候，我们不是除以第一个数据，而是除以所有得到的数据的和的导数，然后也不舍弃小数。首先我们同理得到用正态分布公式计算的结果：

 

然后我们把每一个数除以所有数据的和：

 

这样就获得了canny的卷积核了。

接下来我们导入一张想要获取边缘信息的图片，然后与高斯卷积核做卷积，得到卷积后去除噪声的图像。（估计卷积之后也就是别人说的那样：垃圾图片进，垃圾图片出）

这样第一步完成了。

计算梯度

第二部分是计算图像边缘的梯度，什么叫梯度，就是函数下降最快的方向，用数学表达式就是：

梯度的幅值和方向就是：

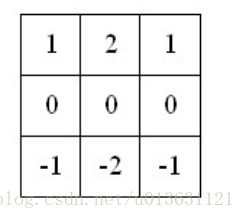
我们知道梯度方向就是两个偏导数之比，但是我们怎么求这个偏导数呢，我们于是引入了sobel算子：

 

这两个就分别是x方向以及y方向的卷积核，也成sobel算子。

至于为什么卷积核的数据是这几个数呢。这里面篇幅比较少，我就简单讲解一下吧：

首先我们假定有一张图片的部分3*3的图片矩阵：

A	B	C
D	E	F
G	H	I

我们把它的坐标定为：

(x-1,y+1)	(x,y+1)	(x+1,y+1)
(x-1,y)	(x,y)	(x+1,y)
(x-1,y-1)	(x,y-1)	(x+1,y-1)

我们假设想要求E点的梯度，那么我们不知道梯度方向是啥，因为这TMD全是离散的数据，那么我们怎么办？Sobel算子的发明人就有个一个想法(也就是下面这个学霸），我们假设它的方向有4个分别是AI方向：

这四个方向分别是(A,I) (B,H) (C,G) (F,D)，然后我们把四个方向给求出来:

(A,I）就是：

[((x-1)-(x+1)),((y+1)-(y-1))]=[-2,2],约分得到[-1,1]。

(B,H）就是：

[(x-x),((y+1)-(y-1))]=[0,2],约分得到[0,1]。

（C,G）就是：

[((x+1)-(x-1)),((y+1)-(y-1))]=[2,2],约分得到[1,1]。

(F,D）就是：

[((x-1)-(x+1)),y-(y)]=[2,0],约分得到[1,0]。

这四个方向哪个是梯度的方向啊？我们也不知道，可能有一个是，也有可能都不是，那么我们怎么办？

我们假设图片上面最中间的值为f(x,y)，那么A,I两点就分别是f(x-1,y+1),f(x+1,y-1)。这两个点的距离是4，为啥，数格子，最短路径是4.也就是x两个格子，y两个格子（因为是离散数据，不能走斜线）。我们用这两个点的数据相减，然后除以4会得到：

f(x-1,y+1)-f(x+1,y-1)/4=(A-I)/4

我们称为AI的方向导数，也就是AI的变化率。

导数值我们求出来了，但是我们这个是一个标量，所以接下来我们要把这个数与方向相乘[-1,1]，获得AI的梯度值，至于为什么相乘就是梯度值，我也不大清楚，应该是作者定的吧。同理我们把(B,H) (C,G) (F,D)都给它求出来，我们得到：

(C-G)/4 * [ 1, 1]

 

(A-I)/4 * [-1, 1]

 

(B-H)/2 * [ 0, 1]

 

(F-D)/2 * [ 1, 0]

这些值我们求完之后呢，我们给这四个值加和，加和之后我们应该除以4求一个平均值作为梯度。但是我们的卷积核是整数，我们不能除，所以我们选择乘以4，给这个平均值扩大16倍，比如X坐标方向的值：

Gx = [(c-g-a+i)/4 + (f-d)/2, (c-g+a-i)/4 + (b-h)/2]

Gx' = 4*Gx = [c-g-a+i + 2*(f-d), c-g+a-i + 2*(b-h)]

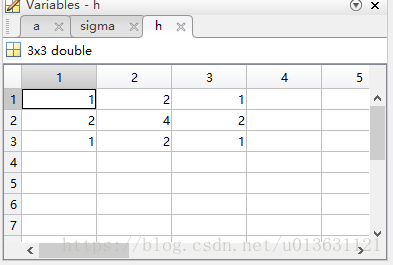
然后我们把相应个字母前面的系数带入到对应的矩阵中，就会得到卷积核：

同理Y的卷积核也可以求出：

至于上面的推导过程，大家不懂的话没有事儿，因为本人也是很懵逼的，尤其是(C-G)/4 * [ 1, 1]相乘，我一直就想不明白，如果大家明白请告诉我哈！

说了这么多，我们还是说以下怎么计算梯度吧：

其实，我们上面已经告诉了，就是4*Gx = [c-g-a+i + 2*(f-d), c-g+a-i + 2*(b-h)] ，也就是我们用高斯处理后的图像与sobel卷积核做卷积，一共有两个卷积核，做卷积后会得出Gx，Gy两个方向的梯度。梯度方向垂直方向就是边缘方向。

非极大值抑制

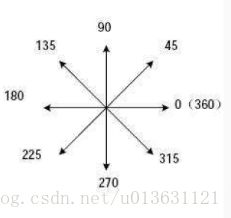
我们计算完成梯度之后，我们要做的就是边缘检测了，怎么检测？首先第一步是要将这张图片的边缘离散化为上下左右斜8个方向：

接下来求出各个方向的梯度这个梯度值的求法和上面的sobel算子差不多，比如90度的话就是用f(90)-f(0)/1，然后乘以它们之间的方向[0,1]。这样就OK了。其它的方向也是如此，我们知道了这个方向以后，下一步是利用公式：

我们Gy，Gx已经用sobel算子求出来了，然后8个方向的梯度G也求出来了，接下来我们假定：

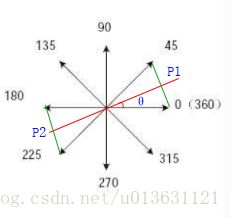
梯度的方向会与G45,G0交于点P1，G225，G180交与点P2，这两个点怎么算？首先我们要以Gy为纵坐标，Gx为横坐标，把G45,G0画到坐标上面，然后我们把这两个点连线，形成一个一次函数Gy=K1*Gx+b1。

然后我们把Gy，Gx的方向作为一个正比例函数Gy=k2*Gx，然后联立，就会求出P1点的坐标。

同理，我们把G225，G180画到坐标上面，然后我们把这两个点连线，形成一个一次函数，然后与Gy，Gx的方向的正比例函数联立，这样P2坐标就求出来了。

接下来我们要判断边缘了：

我们用G（Gy，Gx）与我们就出来的P1,P2进行比较，如果G比P1且P2都大的话，那么说明它可能是边缘，并记录下来。如果要是比其中一个小的话，那就不成立了，直接判断不是边缘！这个方法就叫做非最大值抑制，也就是比其中一个小就给它干掉！

双阈值检测

在非最大值抑制过后，如果这个像素被检测出来可能边缘，那我们还要对它进行的是双阈值检测，怎么检测呢，我们需要手动定义两个阈值，一个是高阈值，一个是低阈值。然后我们用G（Gy，Gx）与阈值进行比较，如果G比高阈值大，那么它就是一个强边缘，如果比高阈值小但是比低阈值大，那么它就是弱边缘。如果比低阈值都小，那么直接判断这个不是边缘。然后把可能是边缘的值都记录下来。

孤立低阈值

我们就这样，可以使用上面的方法检测图片中第一行第一列的像素。但是我们强边缘我们认为一定是边缘了，但是弱边缘一定是边缘吗？不一定，它还需要与其它地方相互比较。我们检测完成第一个像素之后，下一步就是往左边移动一格，检测第二个位置。也是前面4个过程计算完毕。依次类推，第一行最后一格检测完毕后。返回第一行第一列，然后向下移动一格，检测第二行第一列，一直就这么干，直到所有元素都检测完毕。我们检测出一堆边缘。然后我们返回第一个像素，寻找弱边缘的元素，找到一个之后，我们查看弱边缘像素及其8方向的像素，也就是上下左右斜，看看有没有一个元素是强边缘，如果有一个强边缘，那么它就是边缘，如果一个也没有，那么认定它不是边缘。就这样把所有弱边缘过一遍，并且记录。

我们把记录的边缘值高亮显示，其它的值都变为低亮。这样边缘就出来了。

 

最后我们附上代码，这个代码是canny算法的代码：

首先我们有一张图（还是小熊，我最喜欢的小熊了）：

接下来运用代码，进行边缘检测，代码如下：

#导入类库

import cv2

import numpy as np

 

#读入图片

img = cv2.imread("D:/xiaomu/dawawazao.jpg", 0)

#显示图片

cv2.imshow('orgin',img)

#进行边缘检测，设定高低阈值分别为300，200。后把canny边缘图片保存到硬盘，名字为canny.jpe

cv2.imwrite("canny.jpg", cv2.Canny(img, 200, 300))

#显示边缘图片

cv2.imshow("canny", cv2.imread("canny.jpg"))

#按任意键退出

cv2.waitKey()

cv2.destroyAllWindows()
 

最后得到结果：

 

边缘检测本人就讲解完毕了，下节课讲解轮廓检测。

———————————————

如果对我的课程感兴趣的话，欢迎关注小木希望学园-微信公众号： 

mutianwei521

也可以扫描二维码哦！