控制系统与仿真技术(五)-基于 MATLAB 工具箱的控制系统分析与设计
太原理工大学控制系统仿真技术实验报告
1、滑艇的运动学方程为:
![]()
其中, 是滑艇的质量, 是滑艇的牵引力, 为滑艇的运动速度。首先将上述系统线性化,然后使用 LTI Viewer/Linear System Analyzer对以上滑艇系统的动力学方程进行线性分析。
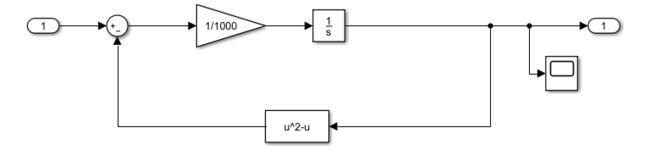
%使用ltiview和sisotool都需要先将模型线性化
[x,u,y,dx]=trim('ex5_1_1',[],[],100,[],[],1);
[A,B,C,D]=linmod('ex5_1_1',x,u);
SS=ss(A,B,C,D);
%[x,u,y,dx]=trim('model',x0,u0,y0,ix,iu,iy)
%[A,B,C,D]=linmod('model',x,u)
%x0初值 ix=1固定
在命令行窗口输入ltiview打开LTI Viewer,如何进去File点击Import,看见下面的页面,会在Workspace里看见上面我们生成的SS,将其导入。

 2、利用单变量系统设计工具Control System Designer,将开环传递函数为
2、利用单变量系统设计工具Control System Designer,将开环传递函数为
![]()
的单位反馈系统的相位裕量提高到50°以上,写出此时控制器的传递函数模型,并画出系统的单位阶跃响应曲线,求出其上升时间、峰值和超调量。
num=40;den=conv([1,0],[1,2])
ex5_2=tf(num,den)
在命令行窗口输入 sisotool打开如下页面
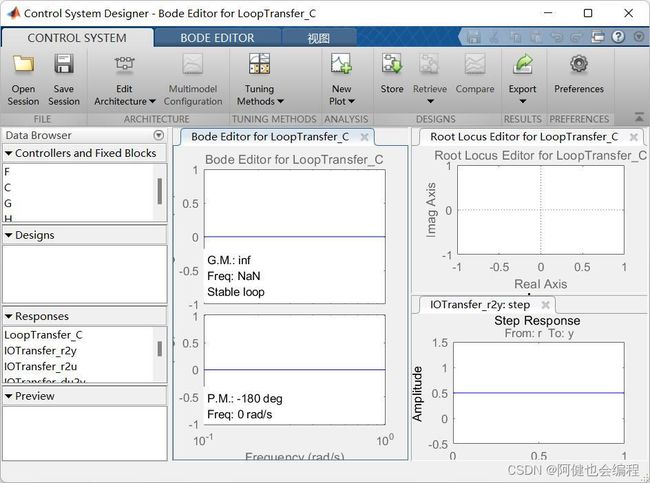 点击Edit Architecture,进入如下页面
点击Edit Architecture,进入如下页面
 将上面生成的ex5_2导入到G中,然后点击OK,产生以下效果
将上面生成的ex5_2导入到G中,然后点击OK,产生以下效果
 下面的操作就是在它的波特图里增加零点(Zero)和极点(Pole)使得相位裕量提高到50以上
下面的操作就是在它的波特图里增加零点(Zero)和极点(Pole)使得相位裕量提高到50以上
 调整后的G可以在Controllers and Fixed Blocks中点击G看出。
调整后的G可以在Controllers and Fixed Blocks中点击G看出。
3、对以下系统,要求系统单位阶跃响应的最大上升时间为10秒、最大调节时间为30秒、最大超调量为20%。利用非线性控制器设计模块(Check Step Response Characteristics)求PID控制器的最佳整定参数Kp、Ki和Kd。假设,三阶线性对象模型的不确定参数:40< a1<50,2.5< a2<10。
其中Check Step Response在Simulink Design Optimization的Signal Constrains中
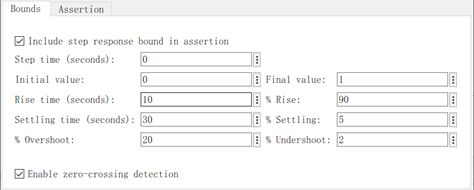
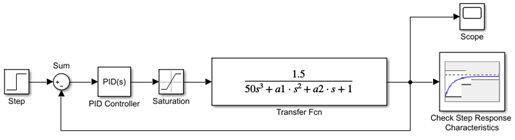 Check Step Response Characteristics参数设置:
Check Step Response Characteristics参数设置:
 改进前的响应曲线:
改进前的响应曲线:
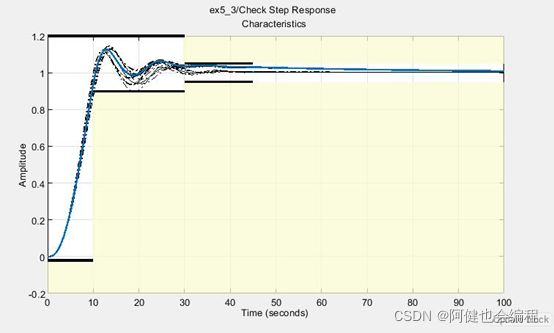
 改进后的响应曲线:
改进后的响应曲线:

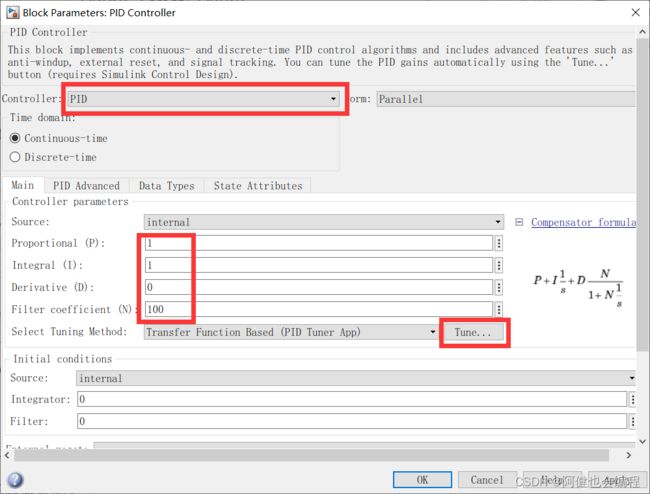
 点击PID
点击PID
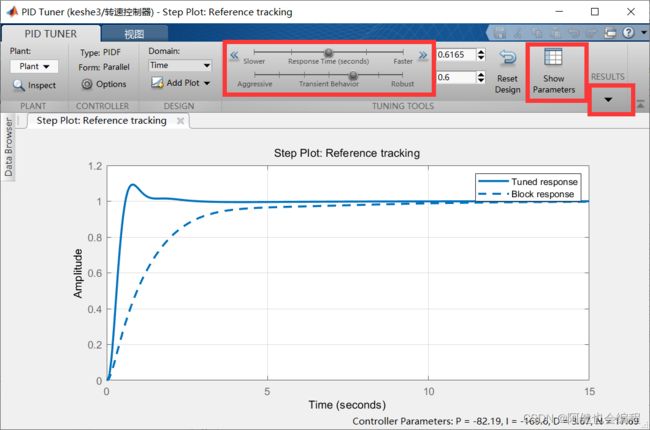 在Results里看到下面结果
在Results里看到下面结果
