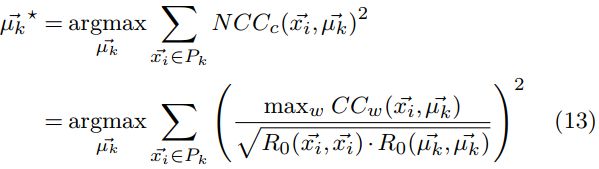【时序聚类】论文解读k-Shape: Efficient and Accurate Clustering of Time Series

k-Shape: Efficient and Accurate Clustering of Time Series

【论文解读有不正确之处欢迎指正】

论文来源：https://dl.acm.org/doi/10.1145/2949741.2949758

论文来自于2016年ACM SIGMOD（有说是2015年，没具体去查），

论文下载：http://www.cs.columbia.edu/~jopa/Papers/PaparrizosSIGMOD2015.pdf

论文代码：（MATLAB）http://www.cs.columbia.edu/~jopa/code/kShapeCODE.zip（需要解压密码，可以联系作者email获取，作者可能是想用这种方式看有多少人关注吧，发个邮件就会给出0258）

1st作者email：[email protected]

几个关于该篇论文的解读网址：

       https://blog.csdn.net/qq_28900249/article/details/84029050（该篇博客分析到第三章）

       https://blog.csdn.net/SCS199411/article/details/90759439（做了简要的分析）

       https://slideplayer.com/slide/8542719/该网站是一个关于此论文的视频介绍，一共13分钟，只看一小部分，可做借鉴

       其他未关于此论文的解读和总结（若有其他资料，欢迎分析）

【论文有理解错误之处欢迎讨论之处，有资料可分享[email protected]】

目录

k-Shape: Efficient and Accurate Clustering of Time Series

Abstract：

1、INTRODUCTION

2、PRELIMINARIES

2.1 Theoretical Background

2.2 Time-Series Invariances（时序数据的几种不变性）

2.3 Time-Series Distance Measures（距离测度）

2.4 Time-Series Clustering Algorithms（序列聚类的算法）

2.5 Time-Series Averaging Techniques（计算序列中心的算法）

2.6 Problem Definition

3. K-SHAPE CLUSTERING ALGORITHM

3.1 Time-Series Shape Similarity（距离测度）

3.2 Time-Series Shape Extraction

3.3 Shape-based Time-Series Clustering

4. EXPERIMENTAL SETTINGS

论文总结

---

 

Abstract：

1、介绍时序聚类的意义和使用价值，跨学科、跨领域的时序数据更加普遍，聚类方法是数据融合中是非常受欢迎的一个方法
2、概括本文方法的特点（homogeneous and well-separated），介绍本文方法的思路，两个创新：距离测度和类质心计算。
3、与其他算法的对比和实验性分析

1、INTRODUCTION

这一部分篇幅较长，可以总结为一下几个部分
1、对时序数据介绍和引入，那些数据可以看做时序数据，另外介绍其使用的领域
2、介绍处理时序数据的方法，回顾各文献中对聚类的关注，引出时序聚类
3、指出时序聚类中时间测度的问题，并利用心电图数据做出解释
4、大多文献在聚类中对距离测度的创新多于对算法的创新，但算法的选择也会影响到准确性和效率
5、介绍本文的算法，k-shape与K-means算法的相同之处与不同之处。相同之处在于都是不断迭代完善的不同在于使用不同的距离测度和质心计算方法
6、实验结果概括，在48种数据库上做实验，并与目前最好的算法进行对比。作者得出与别的文献不同或是相反的结论（in contrast to what has been reported in the literature），指出算法和距离测度一样重要。
7、最后是相关章节的安排

2、PRELIMINARIES

(预备知识，分为6个部分)

2.1 Theoretical Background

Hardness of clustering:
介绍类的两种特性：同质性和分离性（homogeneity and separation【可能翻译不准确】），即为类内元素尽可能相似，类间元素尽可能不相似。作者说最小化SSD（sum of squared distances）可以表达这两者（both）。【貌似表达homogeneity还可以，表达separation有些牵强，或许是理解不到位】

这是一个NP难问题，可以用k-means得到局部最优解，介绍了k-means算法的两个步骤
Steiner’s sequence
序列的中心（即类的中心）计算是一个Steiner的序列问题，新的质心可以最小化SSD，但两个序列的对比需要使用ED或是DTW，质心的求解也是一个NP-complete问题

2.2 Time-Series Invariances（时序数据的几种不变性）

【这部分几个词的翻译不好理解，未想到合适的专业名称】
Scaling and translation invariances：缩放平移不变性

Shift invariance：平移不变性（全局比对和局部比对问题：global alignment and local alignment）【注意作者对translation和shift两个词的使用，虽然汉语翻译相同，但两者对数据的扭曲失真不同】

Uniform scaling invariance：均匀缩放不变性，介绍序列长度的问题，对长序列进行拉伸，对短序列进行压缩

Occlusion invariance：缺失不变性（Occlusion的本意是闭塞的意思），当部分子序列有丢失时，匹对过程中需要将其忽略。

Complexity invariance：复杂不变性。要根据具体使用情况来确定相似性，举出室内和室外语音的例子

2.3 Time-Series Distance Measures（距离测度）

此部分主要介绍ED（欧拉距离）和DTW两种“距离”度量方式，比较简单

2.4 Time-Series Clustering Algorithms（序列聚类的算法）

首先从大层面分析了两种方法，基于原始数据的方法（领域无关）和基于模型的方法（领域相关），提出本文使用的是前一中方法。在基于原始数据的分类方法中又介绍了三种常用的方法，分层聚类, 谱聚类和分区聚类(partitional clustering)。当分区聚类使用的距离测度满足几种不变性时作者将其称为基于形状的方法(shape-based)。最后讨论了分区聚类中的k-means和k-medoids方法的相似和不同之处。

2.5 Time-Series Averaging Techniques（计算序列中心的算法）

对于ED，序列的均值即为算术平均，对于DTW，作者列举了三个其他文献中提到的计算平均序列的方法：Nonlinear alignment and averaging filters (NLAAF)、Prioritized shape averaging (PSA)、Ranking Shape-based Template Matching Framework (RSTMF)。作者也分析了这三个方法的缺点，提出另一个文献上的方法：Dynamic Time Warping Barycenter Averaging (DBA)。作者说以上方法中DBA方法最有效，但最后却说文中使用的是另外一种基于矩阵分解的方法。不知这里的表达逻辑。

2.6 Problem Definition

本文解决的问题是领域无关的，准确的，具有扩展性的时序聚类问题。文中提供的距离测度方法可以提供伸缩平移不变性。

3. K-SHAPE CLUSTERING ALGORITHM

首先介绍了互相性被忽视的现状及其缺陷，本文在计算距离测度时会用到互相关性计算方法。

3.1 Time-Series Shape Similarity（距离测度）

Cross-correlation measure:（互相关性计算）

【补充传统互相关计算方法】

https://www.cnblogs.com/zhxuxu/p/10097620.html

本文作者使用的互相关计算：

两个序列x和y（长度应该可以不同，为了简化作者使用的都是m）:，。固定y不动，使用x序列进行滑动，则

向左或向右滑动后，空缺的的部分补零，互相关计算的结果也是一个序列，，一共2m-1个（w=2m-1）。

k=0时代表无滑动，即x,y刚好相对。此时对于CCw(X,Y)来说刚好w=m，这一点在后面会用到。
利用多种方法对数据进行归一化，包括原始数据x,y和计算得到的互相关序列，

归一化的目的是什么？
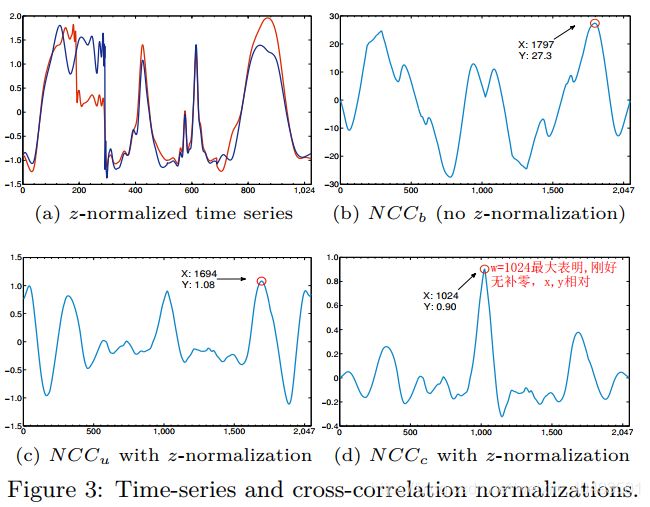
Figure 3a,we remove differences in amplitude by z-normalizing x and y in order to show that they are aligned and, hence, no shifting is required。
Furthermore, as we have seen in Figure 3, crosscorrelation sequences produced by pairwise comparisons of multiple time series will differ in amplitude based on the normalizations.
这是作者提出的几种归一化的作用（先往下看）归一化的结果如图3

用实验结果来说明归一化，bcd三幅图表明NCCc的归一化方法更好，它的峰值在1024，刚好是w=m的点（序列原长为1024）。仔细看这三幅图不太符合对照实验，(b)图使用的是无归一化的原始数据，(c)(d)使用的都是归一化的数据，即如何说明现对原始数据归一化再对互相关序列归一化得到的结果更好，又如何理解此时的峰值为“好”呢（需要进一步学习卷积和互相关性计算）。

随后介绍本文的核心之一，距离测度
Shape-based distance (SBD):

SBD的取值在[0,2]之间，越小说明越相似

Efficient computation of SBD:
分析SBD计算的时间复杂度为，互相关计算与卷积计算类似，因此也可以转化为傅里叶变换和逆变换，使用快速傅里叶计算方法（其他文献中），可以将时间复杂度降为：

3.2 Time-Series Shape Extraction

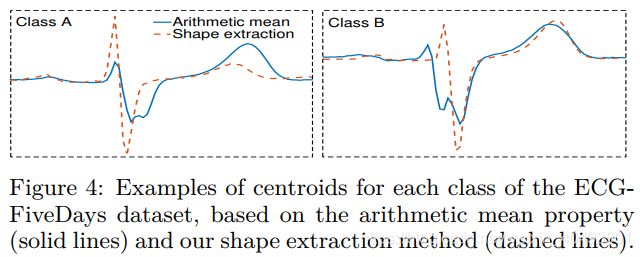
本文的第二个核心，根据SBD来计算类的质心（该质心能够保持类的形状shape和特征），先入为主看结果

图1两个类中分别有两个序列数据，图4中的实线为算术平均，也是k-means中常使用的，该曲线无法反应类的特征，虚线为作者提出的类质心计算方法。【具体推导细节未完全理解，整体逻辑梳理如下】
首先，按照前文提到的误差平方和最小的原理，使类中各序列到质心的SBD的平方和最小。

忽略分母的影响，并根据(6)式和(7)式将（13）式简化

因此（13）式简化为： 

使用向量的表达方式，转化为（14）式

引入矩阵

到此为止，类质心的计算就转化为矩阵M特征值和特征向量的求解了。核心在于（13）式到（14）的推导和（15）的变换。

3.3 Shape-based Time-Series Clustering

本文的最后一个核心，聚类算法以及复杂度介绍。
这一部分比较简单，主要包括两个步骤：Refinement 和 Assigment。一部分使用3.1的算法计算距离测度，在利用3.2的算法计算类的质心进行样本重新分配。逻辑思路和k-means类似，只是计算方式换了

4. EXPERIMENTAL SETTINGS

后面的部分都为实验对比和讨论分析部分。

 

论文总结

1、本文两个创新点，一个是距离测度，一个是质心计算。大多论文中使用的是DTW来计算序列的相关性，但这种算法会有较大的时间复杂度，作者使用互相关来计算。互相关使用的较少，也可以反应序列之间的相似性，但正如作者所说如果设计不好，效果并不如DTW。互相关计算的结果仍是一个序列，使用该序列中的最大值来反应相似度。另外使用一些归一化来消除数据的扭曲和失真。

2、质心的计算。如果用传统的方法算术平均来计算一个类的质心对于序列来说很难反应该类的特征，或者说这种平均值没有意义。作者根据测度来设计质心的计算属于一套组合拳。并将质心的计算从理论公式上推算为计算一个矩阵的特征向量，使得在实践过程更为便捷。利用最小化距离测度来计算计算质心的思路比较好理解，具体推导转化为一个矩阵的过程需要进一步学习理解。

3、论文中的实验对比分析，结果描述部分很完善，对论文习作可以学习。

4、从MATLAB代码转化为python实践正在进行中......