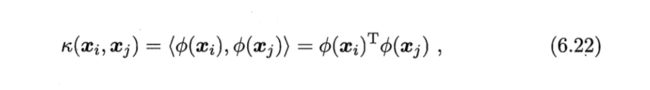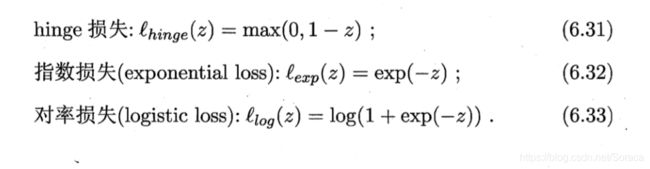Datawhale7月“吃瓜教程“Task05打卡

ps:本文为记录参与Datawhale-7月吃瓜教程的学习笔记

pss:文章所有PPT截图来自于：Datawhale吃瓜教程（https://www.bilibili.com/video/BV1Mh411e7VU），记得一键三连~

目录

Task05 详读西瓜书+南瓜书第6章

1 间隔与支持向量

2 对偶问题

3 核函数

4 软间隔与正则化

5 支持向量回归

6 核方法

---

Task05 详读西瓜书+南瓜书第6章

1 间隔与支持向量

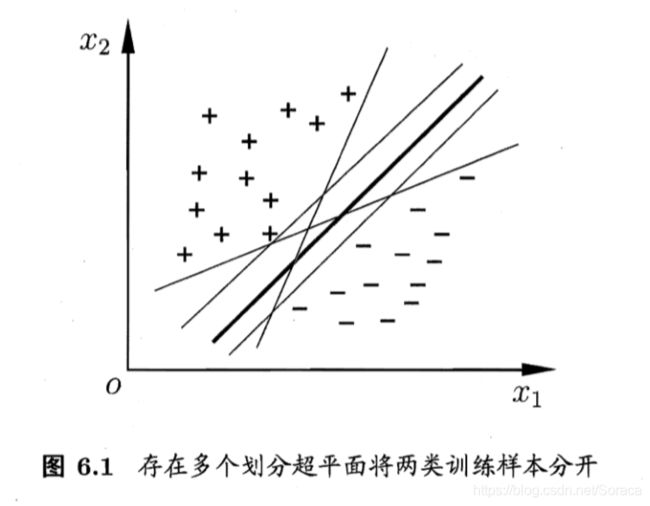
我们想要找到一个样本空间D中的超平面，将不同类别的样本划分开。这样的超平面有很多，但是现在正中的划分超平面对训练样本扰动的“容忍性”更好，更具有鲁棒性，对未见样例的泛化能力最强。

 

 

 

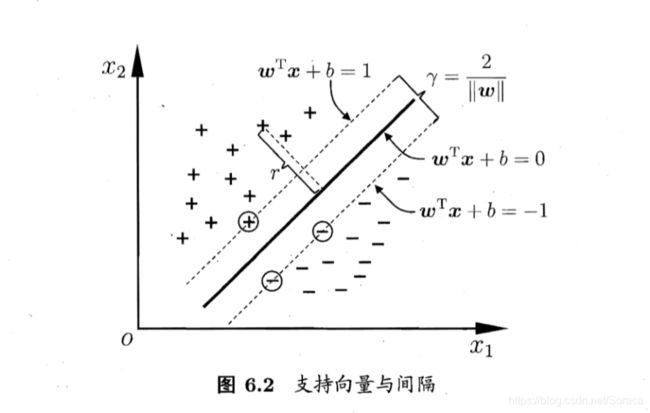
如下图6-2所示，距离超平面最近的几个训练样本点使得公式6.3中的等号得以成立，它们被称为“支持向量 (support vector）”。两个异类支持向量到超平面的距离称为“ 间隔 ”。

 

最优的划分超平面需要使得间隔最大化。

 

这就是支持向量机(Support Vector Machine，简称 SVM)的基本型.

2 对偶问题

对上式6.6使用拉格朗日乘子法可以获得其对偶问题，对式(6.6) 的每条约束添加拉格朗日乘子.该问题的拉格朗日函数可写成下式：

 

 

         

 

求解6.11的时候，因为其是二次规划问题，可以通过二次规划算法求解。带该问题的规模正比于训练样本数，所以在实际任务中开销巨大。因此，有很多规避这一开销的算法。

SMO：
固定α以外的所有参数，求α的极值。通过约束条件，可以用其它变量将阿尔法进行表示。
过程重复以下两步：
1 选取αi、αj
2 固定其它参数，解6.11并跟新αi、αj

αi、αj有一个不满足KKT条件的时候，目标函数就在迭代后减小。违背程度大则变量更新后的目标函数减幅越大。

3 核函数

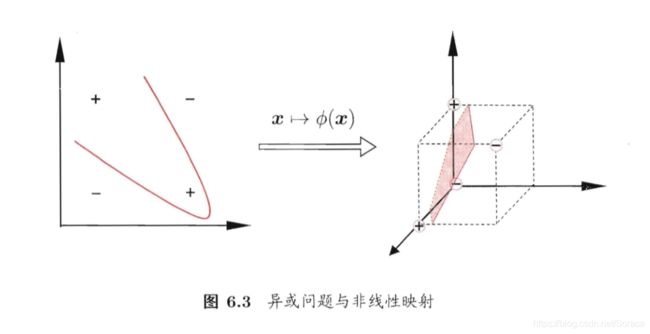
现实任务中，原始样本空间中也许不存在一个可以正确划分两类样本的超平面，但可以通过映射将原始空间映射到更高纬度的空间，进而使得样本在特征空间中线性可分。

例如之前的“异或”问题： 

 

 但是要计算两个x在映射空间的内积比较困难，因为特征空间的往往是高维的。所以我们设想这样的一个函数：

 即两个x在映射空间的内积等于其原始空间中通过k函数计算的结果。这个k函数就是核函数。

 

 

 映射空间的好坏对支持向量机的性能至关重要。在不知道特征映射的形式的时候，我们不知道什么样的核函数合适，所以核函数的选择是支持向量机的最大变数。若将特征映射到了不合适的空间，会导致性能不佳。但又一些基本的经验，例如对文本数据通常用线性核，情况不明是可先尝试高斯核。

核函数通过线性组合和直积的方式得到。

4 软间隔与正则化

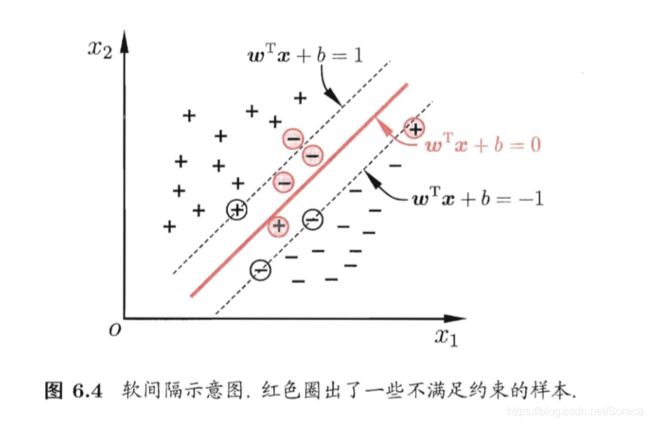
现实任务中很难找到合适的核函数来使得训练集完全线性可分，而且完全的线性可分也可能是过拟合的结果。为了缓解这一问题的一个办法就是允许向量机在一些样本上出错。因此引入了软间隔（soft margin）的概念。

 前面介绍的支持向量机形式是要求所有样本均满足约束(6.3)， 即所有样本都必须划分都正确，这称为"硬间隔" (hard margin)，而软间隔则是允许某些样本不满足约束：

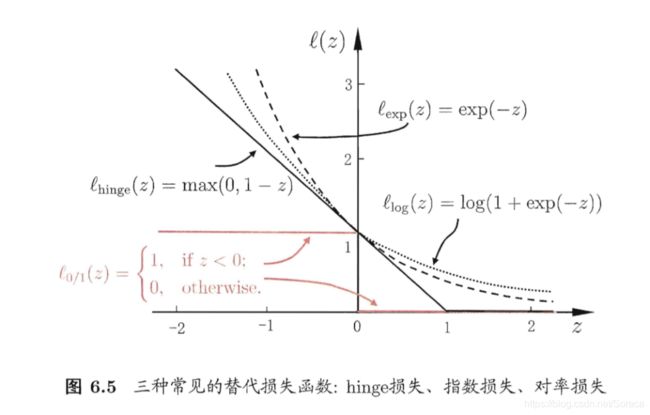
 然而，  非凸、非连续，数学性质不太好，使得式(6.29)不易直接求解.于 是，人们通常用其他一些函数来代替  ， 称为"替代损失" (surrogate loss). 替代损失函数一般具有较好的数学性质，如它们通常是凸的连续函数且是  的上界.图 6.5 给出了三种常用的替代损失函数:

 

 

 

 

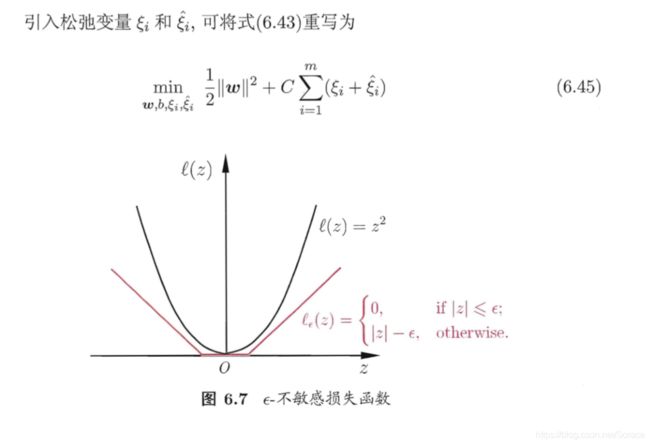
5 支持向量回归

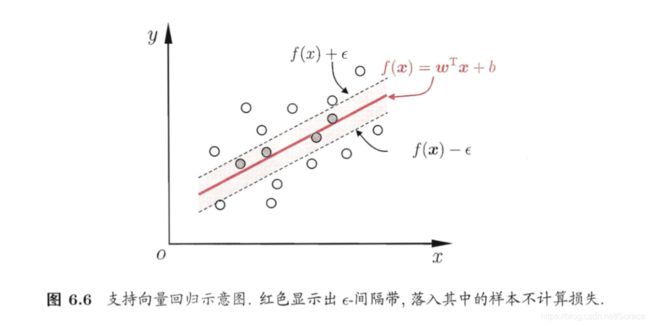
对于传统回归模型，基于模型输出与真实输出y的差别计算误差，SVR中，我们假定容忍一定程度的偏差，仅当模型输出与真实输出的误差绝对值大于时，才计入误差。.如图 6.6 所示，这相当于以为中心，构建了一个宽度为2的问隔带，若训练样本落入此间隔带，则认为是被预测正确的.

 

 

 

 

6 核方法

无论SVM还是SVR学得的模型都能表示为核函数的线性组合，显示出核函数的优势。所以发展出了一系列的基于核函数的学习方法，统称为核方法（kernel methods）。

最常见的是通过“核化”引入核函数，将线性学习器进行非线性学习器。