Python线性回归学习笔记

1.什么是线性回归
2.简单线性回归
3.多元线性回归

一：什么是线性回归

线性回归，是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。其表达形式为y = w’x+e，e为误差服从均值为0的正态分布。（百度百科）
回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。如图是一元线性回归

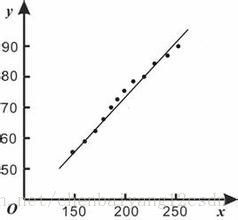
那么这样的统计分析方法有什么实际用处呢？
用一道题来解释：
有一家快递公司送货，送货的历史记录如下
X1： 运输里程 X2： 运输次数 Y：总运输时间

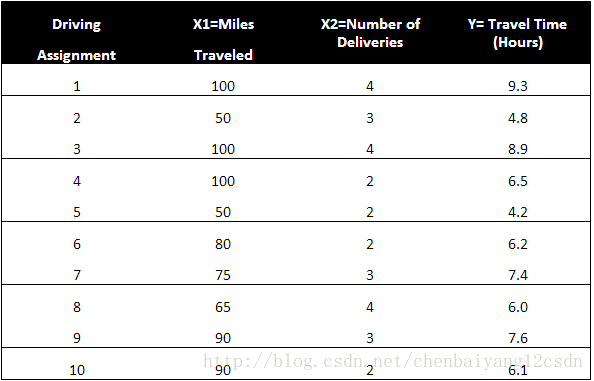
问题来了， 如果一个运输任务是跑102英里，运输6次，预计多少小时？
很显然这是预测问题，即使建立函数y=ax1+bx2+c求出a,b,c即可也无法完全应用于整个数据集，其现实是影响总运输时间的还有运输车的种类、天气、司机等等，这时要找出最适合的函数。

二：简单线性回归

先来看看一个简单的一元线性回归分析问题和python代码实现
假设有一组数据型态为 y=b0+b1x，其中x=[1,3,2,1,3] y=[14,24,18,17,27]

def fitSLP(x, y):
    n=len(x)
    up=0
    down=0
    for i in range(0,n):
        up+=(x[i]-np.mean(x))*(y[i]-np.mean(y))
        down+=(x[i]-np.mean(x))**2
    b1=up/down
    b0=np.mean(y)-b1*np.mean(x)
    return b0,b1

def predict(x,b0,b1):
    return b0+b1*x

x=[1,3,2,1,3]
y=[14,24,18,17,27]
b0,b1=fitSLP(x,y)
print 'b0:',b0,'b1:',b1

x_test=6
y_test=predict(x_test, b0, b1)
print 'y_test:',y_test

运行结果：b0: 10.0 b1: 5.0 y_test: 40.0
可以得到线性回归y=10+5x,当x=6是预计y=40

三：多元线性回归

回到之前提到的快递公司送货问题，这是自变量有两个，这是回归方程y=b0+b1*x1+b2*x,利用sklearn里面的linear_model实现python代码如下

from numpy import genfromtxt
from sklearn import linear_model
#导入数据
dataPath=r'E:\mlresources\express.csv'
deliveryData=genfromtxt(dataPath,delimiter=',')

print deliveryData

X=deliveryData[:,:-1]
y=deliveryData[:,-1]
#建立模型
regr=linear_model.LinearRegression()
regr.fit(X, y)
print "coefficients"  #b1,b2.....
print regr.coef_
print "intercept: "  #b0
print regr.intercept_

xPred=[102,6]
yPred=regr.predict(xPred)
print yPred

运行结果中：
coefficients[ 0.0611346 0.92342537]是系数b1,b2
intercept: -0.868701466782是截距b0

按照 多元回归方程 E(y)=β0＋β１*x1+β2*x2+ … +βp*xp即可构造更多元的回归方程，但是当自变量中有分类型变量(categorical data) , 如何处理？

对于车型来说，有小汽车、SUV、卡车，这是可以用数字0、1、2代表其不同类别，但并不能直接作为自变量输入，需要作出转化成数值型变量

此时数据集如下.csv文件

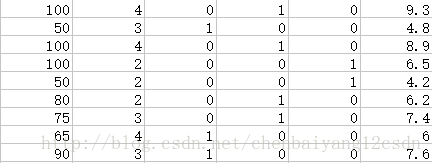
事实上，代码并没有改变。。。。python真好用