pytorch深度学习实战lesson11

第十一课 感知机你太美

目录

理论部分

感知机

60年代的算法

现代感知机算法

感知机的问题：

多层感知机

单隐藏层的多层感知机（单分类）

激活函数的选择

实践部分

从零开始：

简洁实现：

---

上图所示是60年的感知机，可以看到每一个权重都有一根线去传输，可见其工作量之大！现如今肯定有更简洁的方法去实现感知机了，下面让我们和沐神来学一下感知机的原理和设计方法把！！！

理论部分

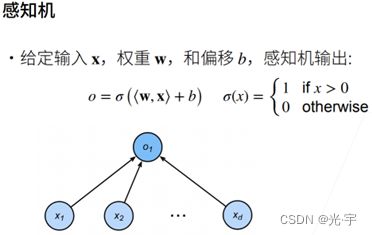
感知机

感知机和线性回归比：

他们的相同点是都有一个输出，但是线性回归输出的是一个实数，但感知机输出的是一个离散的类；

感知机与softmax比：

Softmax输出的是n个元素类别的概率，但感知机只有一个输出，它只能做二分类问题。

60年代的算法

现代感知机算法

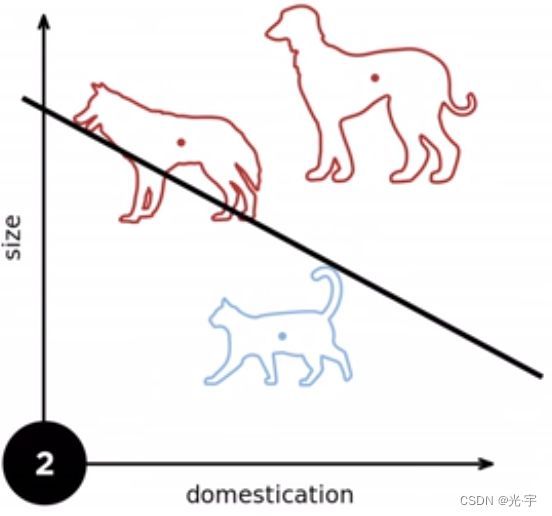
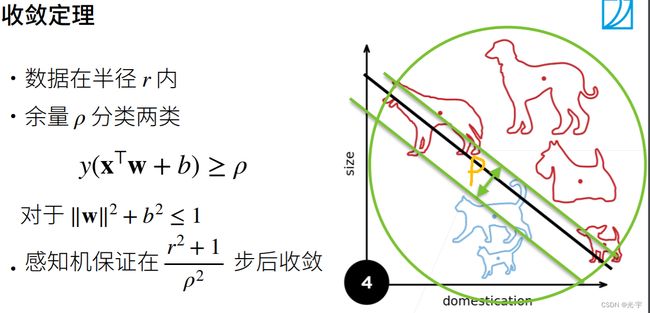
先看一个例子：

                                   

无论来几只狗，几只猫，我都要找到一条准确的“分界线”去将这两类动物进行分类，只是感知器的任务。下面介绍一下感知定理：

两条绿色平行线之间的区域是ρ，这表示的是分界线可以存在的区间，这个区间越大越好，越大就说明两类样本点隔得距离就越大，这样就越容易分类。我们可以看到最后那个收敛公式，是与半径和ρ有关的，当半径越小，ρ越大时它收敛的就越快。当然半径也不能一味的小。

感知机的问题：

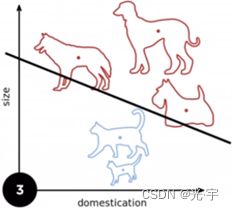
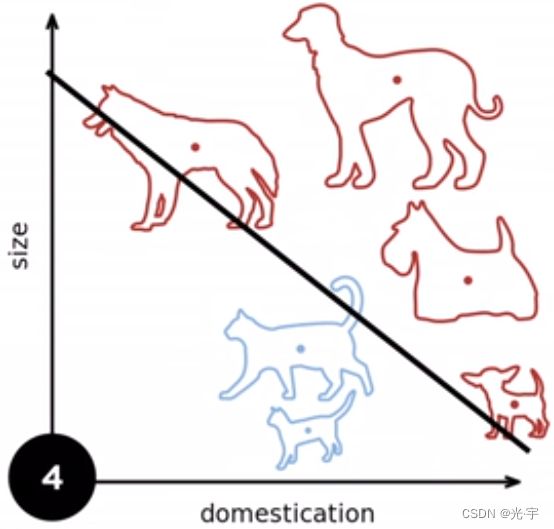
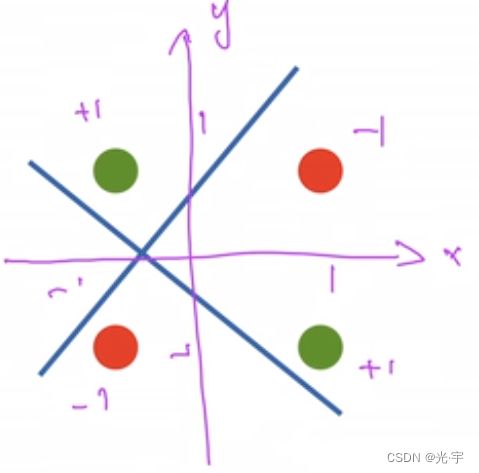
感知机不能拟合XOR函数，它只能产生线性分割面。

感知机不能拟合xor函数，因为它只能产生线性分割面，对于上图所示的数据分布，它无法对红绿进行分类。这就导致了AI的第一个寒冬。具体的历史大家可以参考这篇博客，写的非常好：https://www.cnblogs.com/subconscious/p/5058741.html

在之后的10-15年后，人们研究出了一种能够解决这个问题的办法，那就是——多层感知机。

总结：

1、感知机是个二分类模型，是最早的AI模型之一；

2、它的求解算法等价于使用批量大小为1的梯度下降；

3、它不能拟合XOR函数，导致AI的第一次寒冬。

多层感知机

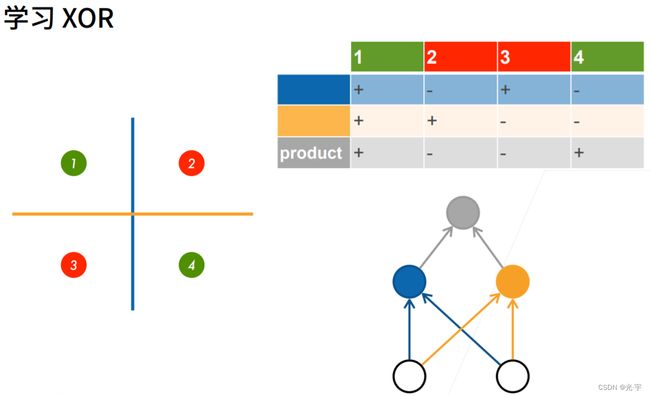
多层感知机处理XOR的方法：

第一层感知机学习蓝线，第二层感知机学黄线，最后一层结合蓝线和黄线就可以得出正确结果了。

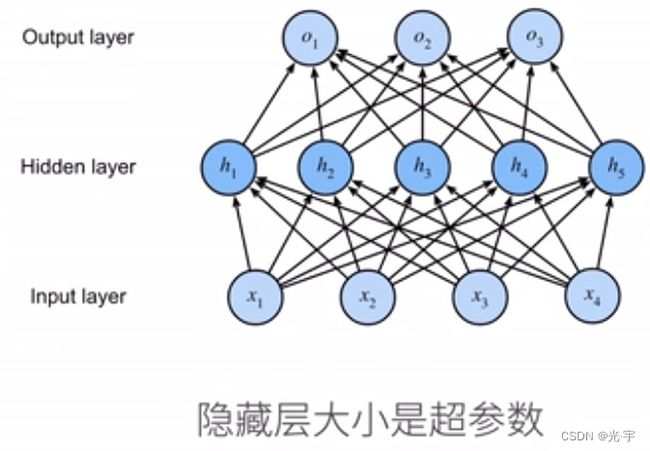
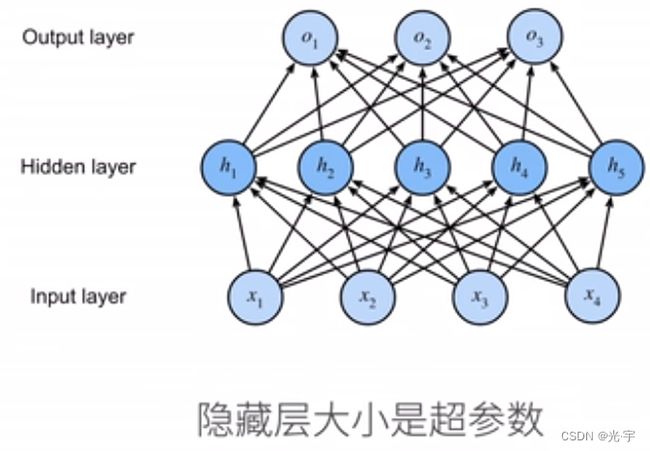
单隐藏层的多层感知机（单分类）

隐藏层有多大可以自己设置。

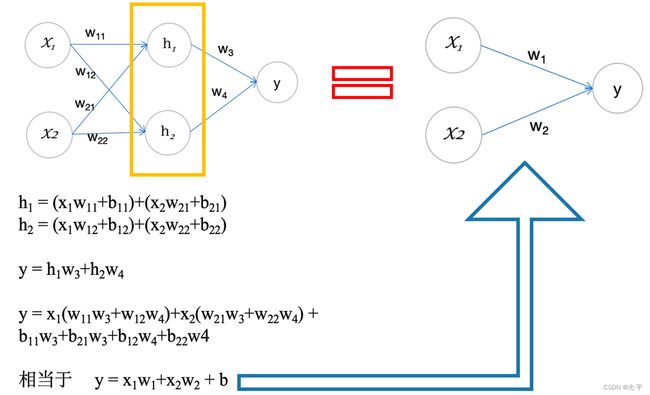
激活函数是非线性的是因为：如果激活函数是线性的话，输出会仍然是线性的，也就是说它会等价于一个单层的感知机。

（神经网络中激活函数的主要作用是提供网络的非线性建模能力，如不特别说明，激活函数一般而言是非线性函数。

假设一个神经网络中仅包含线性卷积和全连接运算，那么该网络仅能够表达线性映射，即便增加网络的深度也依旧还是线性映射，难以有效建模实际环境中非线性分布的数据。

加入非线性激活函数之后，深度神经网络才具备了分层的非线性映射学习能力。因此，激活函数是深度神经网络中不可或缺的部分。）

激活函数的选择

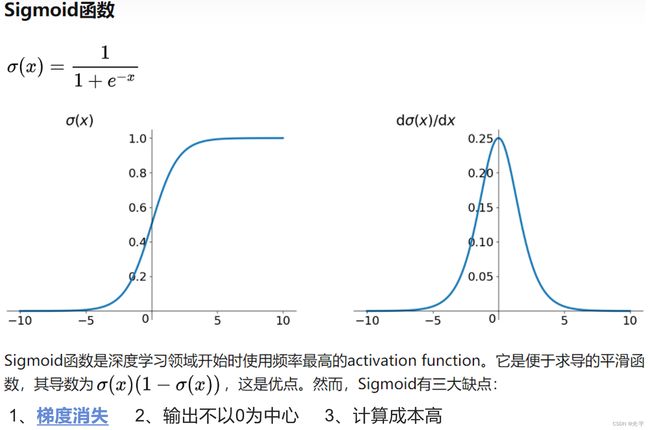
1、sigmoid激活函数

将输入投影到（0,1）中

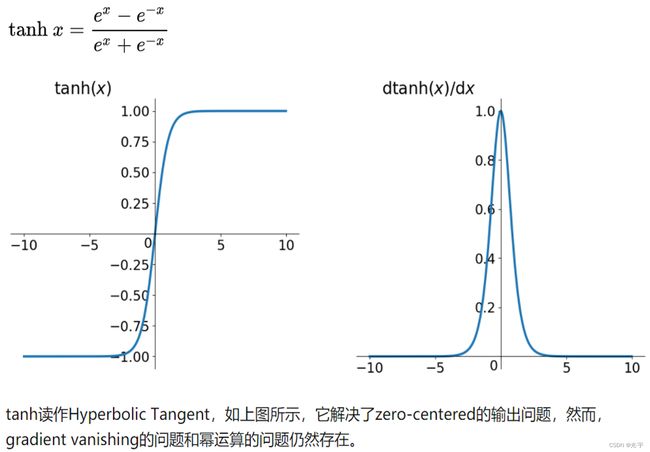
2、tanh函数

将输入投影到（-1,1）

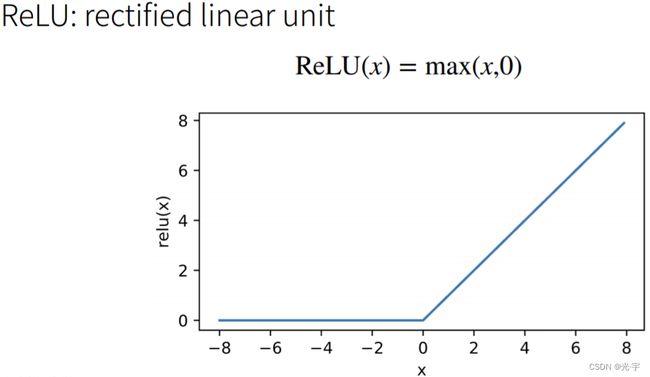
3、relu函数

Relu的运算成本与前俩比很小。

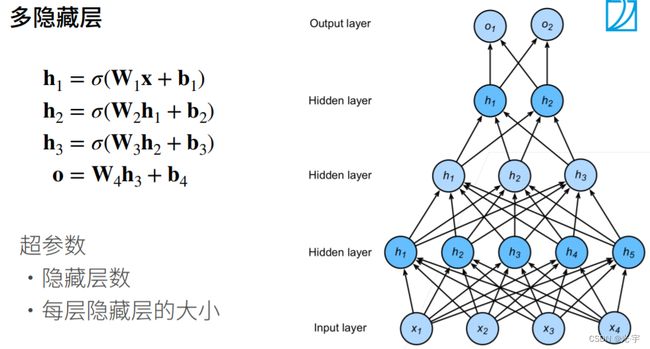
多隐藏层的多层感知机（多分类）

多分类感知机与softmax回归的原理是一样的，唯一的区别就是多层感知机比softmax回归多几层隐藏层。感知机如果我想要返回每个类别的置信度的话，那么它的返回就可以用softmax函数进行处理，这也就是softmax回归了。

如果数据比较复杂的话有两个选择：

第一个选择是单隐藏层，把单隐藏层的维度设高一些；

第二个选择是深化模型（多隐藏层）。

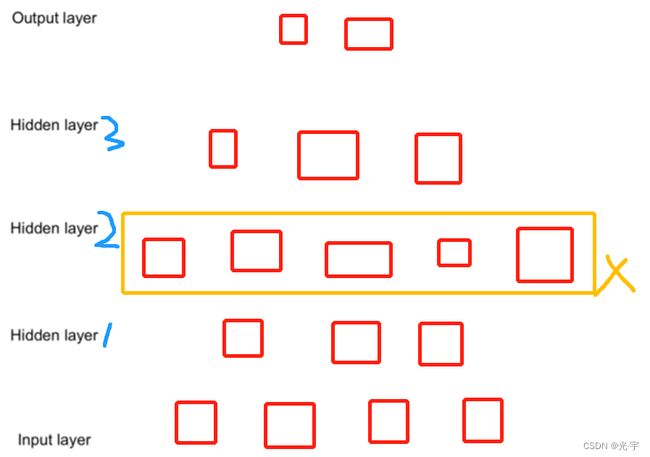
这里每个隐藏层维度的选择是有讲究的，比如下图的hidden layer2就不行，不能“先瘦再胖再瘦”，必须 “先胖再瘦”，因为前者在隐藏层1到隐藏层2的过程中可能会损失很多有用的信息，那么损失有用信息后再增加维度就没什么意义了。

但是沐神说CNN可以有“先瘦再胖再瘦”这种情况，这样可以避免模型overfitting(过拟合)。

实践部分

从零开始：

代码：

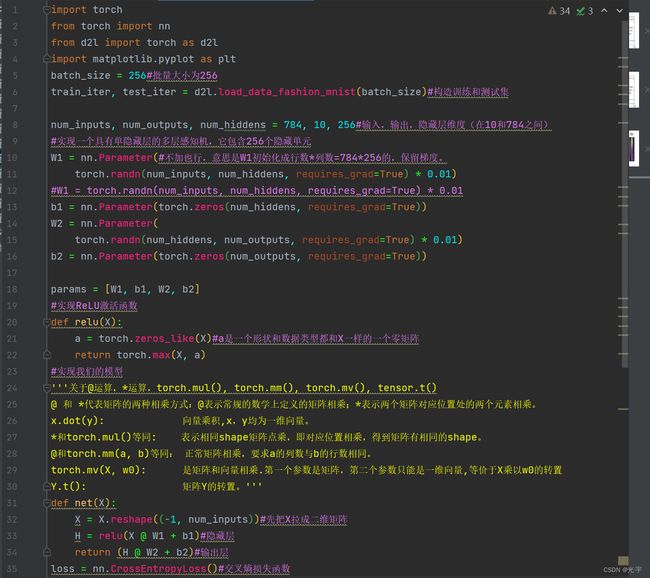
import torch
from torch import nn
from d2l import torch as d2l
import matplotlib.pyplot as plt
batch_size = 256#批量大小为256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)#构造训练和测试集

num_inputs, num_outputs, num_hiddens = 784, 10, 256#输入，输出，隐藏层维度（在10和784之间）
#实现一个具有单隐藏层的多层感知机，它包含256个隐藏单元
W1 = nn.Parameter(#不加也行，意思是W1初始化成行数*列数=784*256的，保留梯度。
    torch.randn(num_inputs, num_hiddens, requires_grad=True) * 0.01)
#W1 = torch.randn(num_inputs, num_hiddens, requires_grad=True) * 0.01
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(
    torch.randn(num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))

params = [W1, b1, W2, b2]
#实现ReLU激活函数
def relu(X):
    a = torch.zeros_like(X)#a是一个形状和数据类型都和X一样的一个零矩阵
    return torch.max(X, a)
#实现我们的模型
'''关于@运算，*运算，torch.mul(), torch.mm(), torch.mv(), tensor.t()
@ 和 *代表矩阵的两种相乘方式：@表示常规的数学上定义的矩阵相乘；*表示两个矩阵对应位置处的两个元素相乘。
x.dot(y):             向量乘积,x，y均为一维向量。
*和torch.mul()等同:    表示相同shape矩阵点乘，即对应位置相乘，得到矩阵有相同的shape。
@和torch.mm(a, b)等同： 正常矩阵相乘，要求a的列数与b的行数相同。
torch.mv(X, w0):      是矩阵和向量相乘.第一个参数是矩阵，第二个参数只能是一维向量,等价于X乘以w0的转置
Y.t():                矩阵Y的转置。'''
def net(X):
    X = X.reshape((-1, num_inputs))#先把X拉成二维矩阵
    H = relu(X @ W1 + b1)#隐藏层
    return (H @ W2 + b2)#输出层
loss = nn.CrossEntropyLoss()#交叉熵损失函数

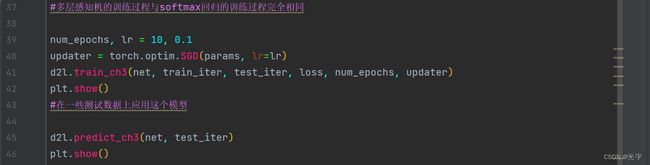
#多层感知机的训练过程与softmax回归的训练过程完全相同

num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
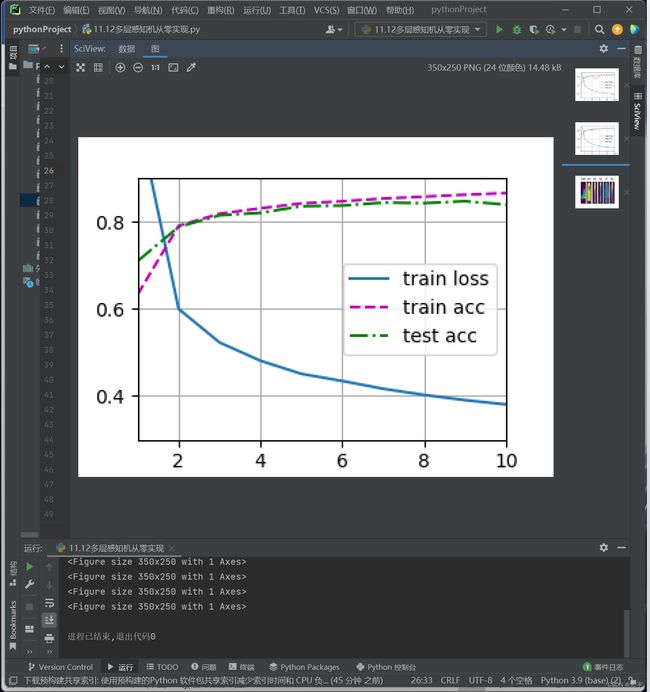
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)
plt.show()
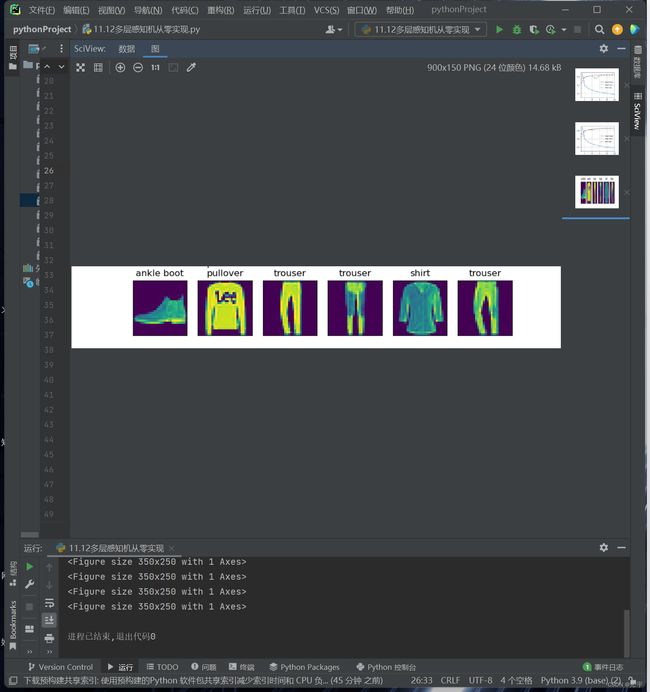
#在一些测试数据上应用这个模型

d2l.predict_ch3(net, test_iter)
plt.show()

简洁实现：

代码：

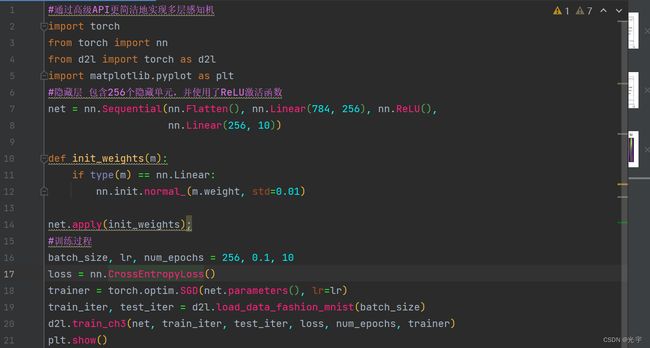
#通过高级API更简洁地实现多层感知机
import torch
from torch import nn
from d2l import torch as d2l
import matplotlib.pyplot as plt
#隐藏层 包含256个隐藏单元，并使用了ReLU激活函数
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 256), nn.ReLU(),
                    nn.Linear(256, 10))
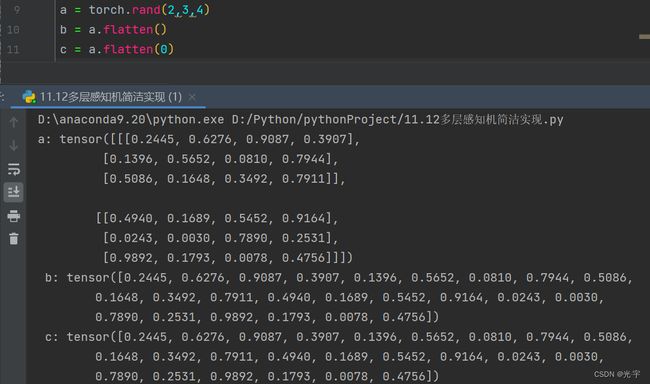
a = torch.rand(2,3,4)
b = a.flatten()
c = a.flatten(0)
print('a:',a,'\n','b:',b,'\n','c:',c)
def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);
#训练过程
batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss()
trainer = torch.optim.SGD(net.parameters(), lr=lr)
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
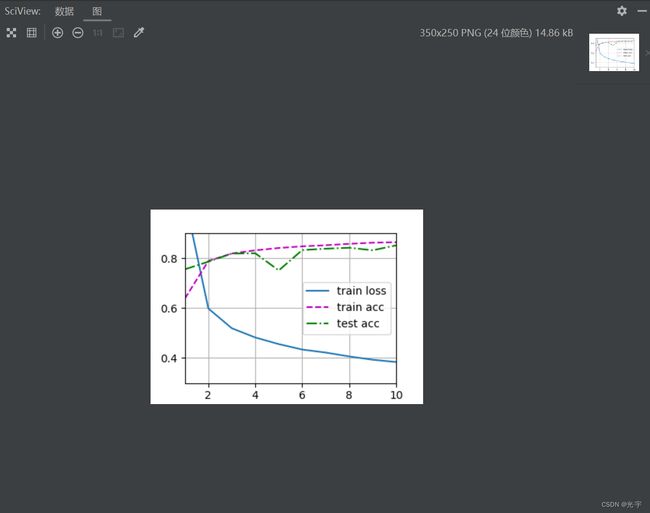
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
plt.show()

Flatten的用法：