小白的逻辑回归学习笔记（入门）

很早之前就有写博客来记录自己学习的过程，入machine learning的坑也有一年了，在理论与实践上也有了一定的积累（其实主要是实践，理论水平还在积极补救），恰逢最近有时间参加了DataWhale的组队学习活动，以任务的形式push着我写下了第一篇博客。后续有时间的话还会多分享所学，请大家多多指教。

逻辑回归简介

开头先着重强调，逻辑回归是分类算法啊！虽然在数学建模中，Logistic模型好像也叫逻辑回归来着，可以用来拟合生物种群繁衍、生物生长发育、疾病传播等等的回归问题，毕竟自然界中绝大多数的事物都符合“S曲线”的发展规律，但这跟在机器学习中广泛应用的逻辑回归差别不小。机器学习中的逻辑回归实际上是Logistic 分布中位置参数为0，尺度参数为1的特例（即Sigmoid函数）。其次，基于Logistic回归的生长模型是拟合Logistic 分布，而机器学习中的逻辑回归是以y=wx+b的基本回归方程作为Sigmoid函数的输入。网上很多博客也没有对两者作出一些比较，搜索逻辑回归的话，以上两者都会被搜出来，这一点感觉较容易混淆。

言归正传，机器学习中的逻辑回归看着挺简单，也比较好理解，sklearn或者各大深度框架中调用一下就完事了，但深究其原理，还是太多太多东西要去学习了，特别是看了这位大佬的文章，膝盖已经在地上了。正因为逻辑回归的可解释性非常强，处理速度比较快，而且比较容易实现并行，目前在众多领域仍具有重要地位，仍作为众多应用场景的基准算法，例如现今国际通用的ICU风险监测手段——APACHE IV评分就是利用多变量逻辑回归来估计患者ICU内死亡的概率所建立起来的模型。除此之外，由于逻辑回归后输出值位于0与1之间，具有概率意义，使模型的输出结果具有概率可解释性，特别是在需要强解释性的场景中，例如医疗应用场景中，往往只提供一个正或负的结果是不够的，还必须告诉医生正、负的程度，概率表示便能满足此要求，因此逻辑回归或者Sigmoid层作为许多机器学习模型的标准配件。

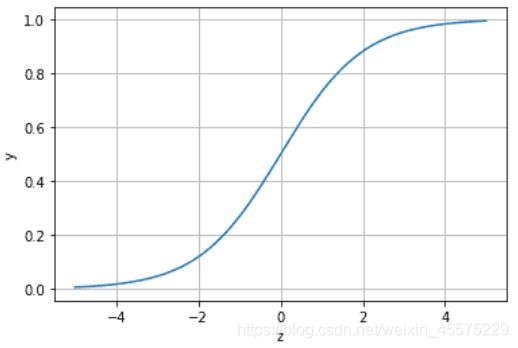
先直观了解Sigmoid函数长啥样：

import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-5,5,0.01)
y = 1/(1+np.exp(-x))

plt.plot(x,y)
plt.xlabel('z')
plt.ylabel('y')
plt.grid()
plt.show()

函数表达式长这样（注意z为基本回归函数）：
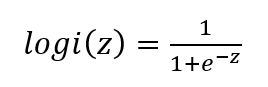此函数导数有以下等式（推BP算法什么的很常用）：

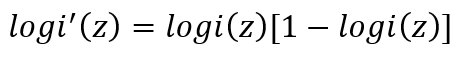
通过观察函数表达式以及函数图像，很明显可以得出当z≥0 时,y≥0.5,分类为1，当 z<0时,y<0.5,分类为0的结论，即逻辑回归引入了y=0.5的决策边界。z的值越大则被分类为1的可能性越大，z的值越小则被分类为0的可能性越大。对于逻辑回归中的参数，一般用最大似然函数来估计，而逻辑回归的对数最大似然函数是一个凸函数，故可用各种梯度下降的优化算法来求解。多变量逻辑回归的话相当于就是one vs rest或者many vs many的过程。（理论部分上面说的那位大佬真的讲得非常详细）

逻辑回归代码示例

下面示例基本展示了逻辑回归的python实现过程：

import numpy as np 
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import metrics
##利用sklearn中自带的iris数据作为数据载入
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
data = load_iris() #得到数据特征
iris_target = data.target #得到数据对应的标签
iris_features=pd.DataFrame(data=data.data,columns=data.feature_names) #转化为DataFrame格式

## 合并标签和特征信息
iris_all = iris_features.copy() ##进行浅拷贝，防止对于原始数据的修改
iris_all['target'] = iris_target

## 合并标签和特征信息
iris_all = iris_features.copy() ##进行浅拷贝，防止对于原始数据的修改
iris_all['target'] = iris_target

##选择其类别为0和1的样本（不包括类别为2的样本）
iris_features_part=iris_features.iloc[:100]
iris_target_part=iris_target[:100]
##测试集大小为20%，80%/20%分
x_train,x_test,y_train,y_test=train_test_split(iris_features_part,iris_target_part,test_size=0.2,random_state=2020)

##定义逻辑回归模型
clf=LogisticRegression(random_state=0,solver='lbfgs')
##训练模型
clf = clf.fit(x_train, y_train) #其拟合方程为 y=w0+w1*x1+w2*x2+w3*x3+w4*x4

##查看逻辑回归模型训练后的权重w
print('逻辑回归模型训练后的权重w为:',clf.coef_)
##查看逻辑回归模型训练后的截距项w0
print('逻辑回归模型训练后的截距项w0为:',clf.intercept_)

##在训练集和测试集上分布利用训练好的模型进行预测
train_predict=clf.predict(x_train)
test_predict=clf.predict(x_test)

##输出预测的概率值
test_predict_proba=clf.predict_proba(x_test)

print('逻辑回归在训练集上的准确度为:',metrics.accuracy_score(y_train,train_predict))
print('逻辑回归在测试集上的准确度为:',metrics.accuracy_score(y_test,test_predict))

confusion_matrix_result=metrics.confusion_matrix(test_predict,y_test)
print('混淆矩阵为:\n',confusion_matrix_result)

多分类时的调用也是一样的，不过对应多个逻辑回归模型，例如3分类对应3个逻辑回归模型（相当于做了3次one vs rest）LogisticRegression的各参数说明可以参考sklearn官方文档，或者参考下这篇文章，讲的非常详细。

逻辑回归部分要点总结

sigmoid的优缺点总结

优点：
1、将预测范围压缩至[0,1]
2、使模型更加关注分类边界（只在0附近敏感）
3、作输出层时使模型结果具有概率上的解释性

缺点：
1、容易造成梯度消失
2、由于Sigmoid以0为中心，梯度为全正或全负，优化时为“之”字线路， 故寻找最优参数耗时较长
3、包含指数函数，计算代价较高

关于逻辑回归的其它要点

离散化
LR 属于广义线性模型，表达能力有限，离散化后每个变量有单独的权重，这相当于引入了非线性，能够提升模型的表达能力，离散后特征可以进行特征交叉，提升拟合能力，且特征离散后模型鲁棒性更强，相当于引入了正则化。

与其它模型的对比（线性回归、SVM、最大熵模型）以及逻辑回归的并行运算，上面提到的那位大佬讲得非常详细。

Reference

【机器学习】逻辑回归（非常详细）

种群竞争模型 — (Lotka-Volterra模型) Logistic回归

Sklearn-LogisticRegression逻辑回归

《深度学习原理与Tensorflow实践》黄理灿

《机器学习实战—基于Sophon平台的机器学习理论与实践》星环科技人工智能平台团队

代码部分参考DataWhale教程