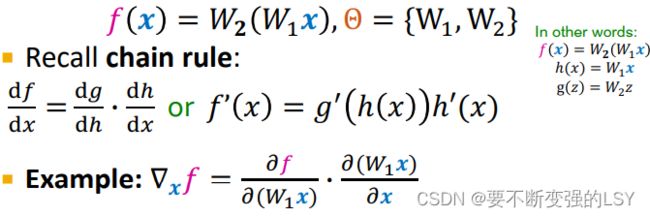【从零开始】CS224W-图机器学习-2021冬季学习笔记6.1 Graph Neural Networks 1: GNN Model——深度学习基础

系列文章目录

【从零开始】CS224W-图机器学习-2021冬季学习笔记1：Machine Learning for Graphs

【从零开始】CS224W-图机器学习-2021冬季学习笔记3.1：Node Embeddings 

【从零开始】CS224W-图机器学习-2021冬季学习笔记3.2：Node Embeddings

【从零开始】CS224W-图机器学习-2021冬季学习笔记13.1：Community Structure in Networks

【从零开始】CS224W-图机器学习-2021冬季学习笔记13.2：Community Structure in Networks——BigCLAM算法

---

课程主页：CS224W | Home
课程视频链接：斯坦福CS224W《图机器学习》课程(2021) by Jure Leskovec

文章目录

1  节点嵌入回顾

2  图神经网络模型——GNN简介

3  深度学习基础知识

3.1  引言

3.2  机器学习模型

3.2.1  有监督学习模型

3.2.2  损失函数举例：交叉熵函数

3.3  梯度下降

3.3.1  梯度和方向导数

3.3.2  梯度下降

3.3.3  随机梯度下降（SGD）

3.4  神经网络函数

3.4.1  反向传播

3.4.2  非线性

3.4.3  多层感知机（Multi-layer Perceptron，MLP）

4  总结

5  参考资料

---

1  节点嵌入回顾

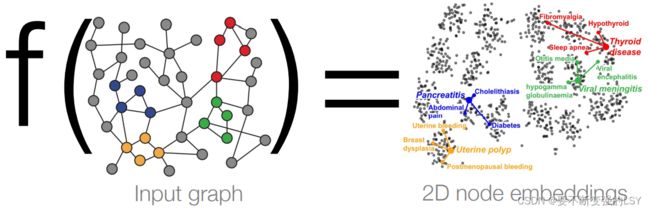
之前我们一直在讨论节点嵌入的任务，其目的在于将每个节点映射到一个d维向量，使得在图中相似的节点在嵌入的向量域中也相似。

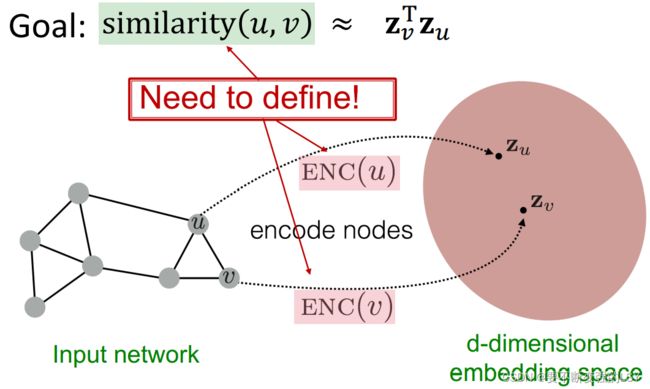
我们还进一步讨论了 编码器-解码器框架：

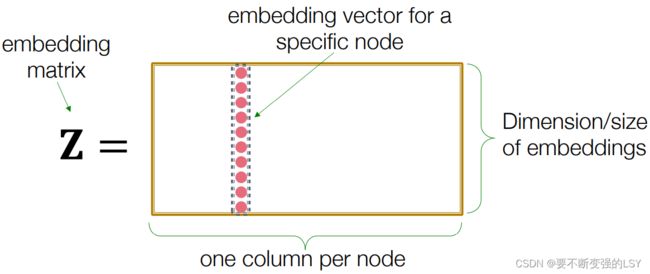
我们还介绍了一种最简单的编码器“Shallow” Encoding，即把编码器看成一个嵌入查找表，也就是使用一个大矩阵Z直接储存每个节点的嵌入，通过矩阵与向量相乘来确定每个节点的嵌入：

但这种浅层的编码方式存在很多局限性：

• 需要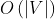复杂度（向量维度×节点数|V| ）的参数，节点之间的参数无法共享，每个节点的表示向量都是完全独特的，对于巨大的图，参数空间也是巨大的；
• 转换的过程是固定的，对于没有出现过的节点，无法生成它们的嵌入，所以无法将一个图的嵌入转移到另一个图，不具有扩展性；
• 无法利用节点中包含的特征信息。

正因为这些局限性，我们将要讨论——深度图编码器(Deep Graph Encoders)，也就是用图神经网络（Graph Neural Networks，GNNs）来进行节点嵌入。

---

2  图神经网络模型——GNN简介

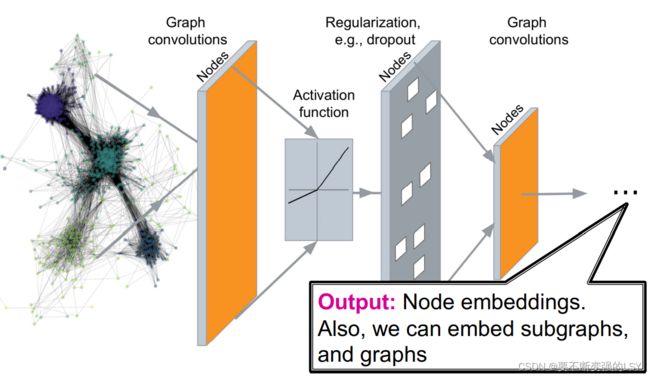
使用GNN进行节点嵌入时，我们得到的嵌入将是一个基于图结构的多层非线性转换：

注：在使用这些深度图编码器时，对节点相似度的定义仍然可以使用之前第3课中学过的方法，比如基于随机游走的相似度函数。

GNN模型的大概框架：

这种编码方式得到的嵌入同样可以在以下任务中取得好的效果：

1. 节点分类：预测节点的分类
2. 链接预测：预测两节点是否相连
3. 社区发现：识别密集链接的节点簇
4. 网络相似性：度量两个图或子图间的相似性

---

3  深度学习基础知识

3.1  引言

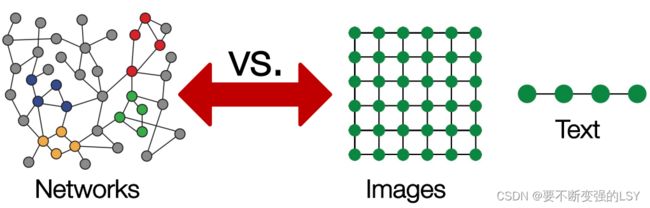
在现代的机器学习工具箱中，传统的深度学习方法擅于处理像图片那样固定大小的矩阵或网格图、还善于处理像文字或语音那样的线性序列。
而相比于这些简单的数据类型，网络（图）通常具有任意的大小，复杂的拓扑结构，节点间也没有固定的顺序，有时还是动态变化的，这就导致很难直接将现在的深度学习框架直接应用于网络上。

3.2  机器学习模型

3.2.1  有监督学习模型

注：这里以回归任务为例定义损失函数

关于L1和L2损失函数的介绍请参考：L1和L2损失函数

二范数（即欧几里得范数）：
(指空间上两个矩阵向量的直线距离)

3.2.2  损失函数举例：交叉熵函数

由交叉熵公式可知，当时，对应的；当时，越接近1，从负值越接近0，越小，也就是loss越小，预测值越接近真实值。

3.3  梯度下降

3.3.1  梯度和方向导数

• 方向导数：函数在某个给定方向上的变化率。
• 梯度：梯度方向是函数变化率最大的方向，函数在这个方向的方向导数达到最大值

方向导数的定义及其与梯度的关系-参考资料：
导数、微分、偏导数、全微分、方向导数、梯度的定义与关系

3.3.2  梯度下降

• 迭代算法：将参数向梯度反方向重复更新，直到收敛
• 训练过程：梯度下降的过程就是优化训练参数的过程
• 学习率(LR)：训练前设置好控制梯度下降每一步步长的超参数，可在训练过程中改变
• 算法终止条件：梯度为0（在实践中，一般是用“验证集上的表现不再提升”作为停止条件）

为什么朝梯度的反方向移动?
当梯度大于0，说明此时坡面朝上，下坡的策略是往坡面的负方向移动；当坡度小于0，说明此时坡面朝下，下坡的策略是往坡面的正方向移动。

3.3.3  随机梯度下降（SGD）

在一般的梯度下降算法中，计算精确的梯度需要遍历整个数据集上的x（损失函数统计的是所有训练数据中的损失总和），而现代数据集通常包含上亿个节点，让计算花费昂贵且速度缓慢。

所以引入随机梯度下降算法（SGD）：将训练集分成多个小批量数据集(minibatch)，对于梯度下降中的每一步，只使用一个minibatch当作输入x来进行计算。

SGD是所有梯度的无偏估计，但是不能保证收敛，所以在实践中常常需要调整学习率。

许多常用优化器都是在SGD的基础上改进的，如：Adam，Adagrad，Adadelta，RMSprop……等

概念解释：

1. batch size：每个minibatch中的数据点数
2. iteration：在一个minibatch上做一次训练（完成一步梯度下降）
3. epoch：在整个数据集上做一次训练

注：在一个epoch中，迭代次数为

3.4  神经网络函数

在深度学习中，神经网络通常会特别复杂，所以这里为了简化，只考虑线性函数：

• 当返回一个标量时，的梯度是一个可学习的向量；
• 当返回一个向量时，的梯度是一个可更新的权重矩阵（雅可比矩阵）；

3.4.1  反向传播

 以一个两层的线性网络为例：（根据求偏导数中的链式法则传播梯度）

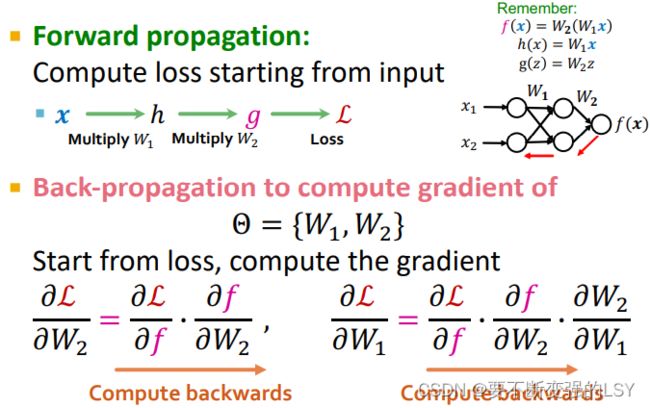
 进一步地得到损失函数：

• 前向传播：从输入计算输出，用输出计算损失函数的过程
• 反向传播：计算梯度的过程（对参数求偏导的过程）

反向传播在李宏毅的机器学习课中讲的更清楚： 7: Backpropagation_哔哩哔哩_bilibili

参考文章：反向传播(Backpropagation)算法详解

3.4.2  非线性

w.r.t：with respect to的缩写，“关于；谈及，谈到”

引入非线性的原因请参考：

• 机器学习-神经网络为什么需要非线性(激活函数)
• 机器学习入门：神经网络为什么要非线性

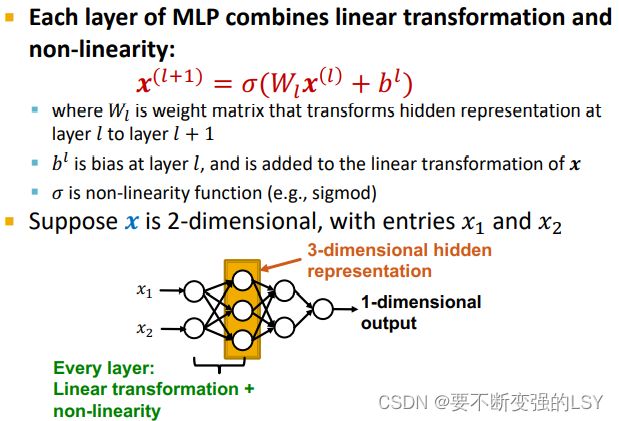
3.4.3  多层感知机（Multi-layer Perceptron，MLP）

MLP的每一层都是线性转换和非线性的结合

 

---

4  总结

5  参考资料

http://web.stanford.edu/class/cs224w/slides/06-GNN1.pdf

cs224w（图机器学习）2021冬季课程学习笔记7 Graph Neural Networks 1: GNN Model_诸神缄默不语的博客