深度学习之图像分类（二十九）-- Sparse-MLP网络详解

深度学习之图像分类（二十九）Sparse-MLP网络详解

本文再次讲述一篇新的 Sparse-MLP 工作，其的 Sparse 主要描述在感受野层面，与 MLP-Mixer 的全局感受野相比，本网络的感受野是轴向的，所以是稀疏的。本文可以看作是 ConvMLP 和 ViP 的结合，但是其发布时间早 ConvMLP 一周。

1. 前言

自 AlexNet 提出以来，卷积神经网络(CNN)一直是计算机视觉的主导范式。随着 Vision Transformer 的提出，这种情况发生了改变。ViT 将一个图像被划分为不重叠的 patch，并用线性层将这些 patch 转换为 token，然后输入到 Transformer Block 中进行处理。无卷积的 Vision Transformer 主要存在两个核心的思想：全局依赖性建模很重要 ；自注意力机制很重要 。但是近期的工作也发现局部依赖性似乎对图像更好（例如 Swin，AS-MLP 等等），或者说局部依赖性是全局依赖性的特殊情况，全局依赖性有要在超大规模训练上才得行。那么这种情况下，似乎还是要注入局部依赖性。此外，自注意力机制计算量是 token 数量的平方量级，因此，网络结构不有利于高分辨率输入，否则计算量 hold 不住（所以 Swin 用来金字塔结构和多阶段处理）。MLP-Mixer继承了ViT的所有缺点（除了自注意力机制中的平方计算量级），且由于参数数量过多，容易发生过拟合 。那么，一个无自注意力机制的网络能否达到 Sota 的性能？

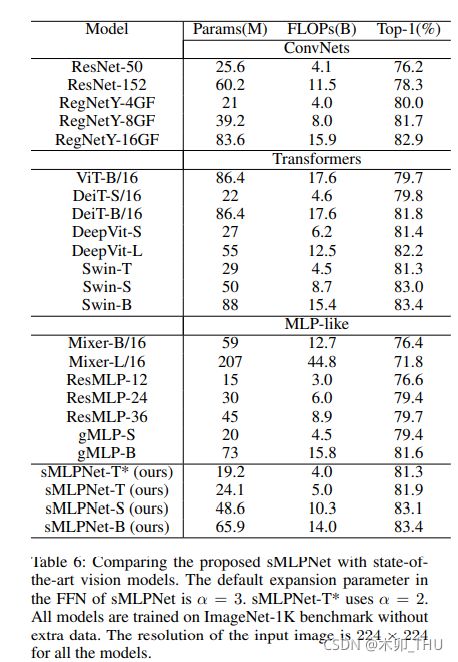
本文就在于提出这样一个网络。本工作的原始论文为 Sparse MLP for Image Recognition: Is Self-Attention Really Necessary?。2021.9.12 挂上 arXiv。其延续 MLP-Mixer 的交替使用 Token-Mixing MLP 和 Channel-Mixing MLP 的结构，不同之处在于修改了 Token-Mixing MLP。在 Token-MLP 中引入了 DWConv（类似于 ConvMLP） 和 轴向映射（类似于 ViP），此外使用了金字塔结构。最终 sMLPNet 在只有 24M 参数下达到 81.9% 的 Top-1 精度，比相同模型大小约束下的大多数 CNN 和视觉 Transformer 要好得多。当扩展到 66M 参数时，sMLPNet 达到了 83.4% 的 Top-1 精度，这与 SOTA 的 Swin Transformer 相当。

2. sMLPNet

2.1 整体网络结构

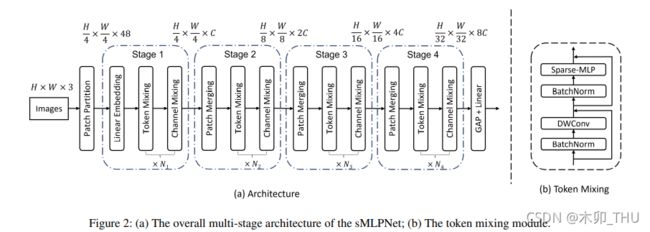
sMLPNet 采用多阶段金字塔模型，总共分为 4 个阶段，每个阶段交替使用 Token-mixing MLP 和 Channel-mixing MLP。Channel-mixing MLP 其实和 ViT 的 FFN 以及 MLP-Mixer 的 Channel-mixing MLP 其实是一样的，两个全连接中间有个 GELU，再加个残差结构。sMLPNet 网络结构图如下所示：

作者一共提出来了三种配置：

• sMLPNet-T: C = 80, number of layers = [2; 8; 14; 2],
• sMLPNet-S: C = 96, number of layers = [2; 10; 24; 2],
• sMLPNet-B: C = 112, number of layers = [2; 10; 24; 2]

其中 $C$ 为通道数目，后面的为每个阶段 Block 重复的次数。

2.2 Token-mixing MLP

sMLPNet 的一大核心在于修改了 Token-mixing MLP。修改后的 Token-mixing MLP 包含两部分：

• BN 前置归一化 + $3\times 3$ DW 卷积 + 残差模块
• BN 前置归一化 + Sparse-MLP 模块 + 残差模块

DW 卷积能有效减少参数量，并且实现局部的信息交流，而 Sparse-MLP 则在轴向上具有长距离依赖。

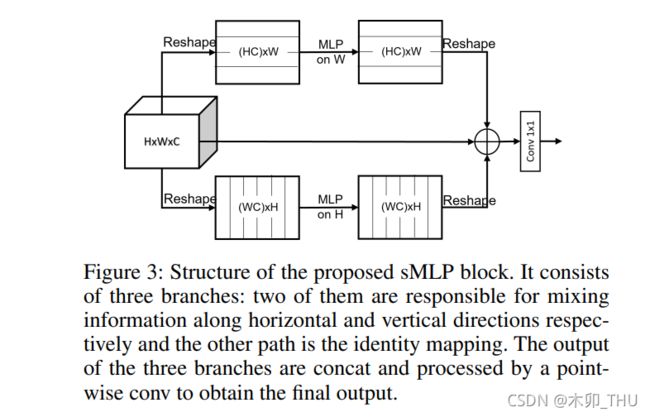
Sparse-MLP 的结构图如下所示，其包含三个部分的并行结构：W 通道映射，H 通道映射，不动。这其实与 ViP 的三条并行支路很像，唯一不同的是 ViP 的第三条支路为通道 $1\times 1$ 卷积，而 Sparse-MLP 中为恒等映射。三条并行支路被通道拼接连在一起，然后经过一个 $1\times 1$ 卷积将通道数变为 1/3，即保持输入输出一致。

不难发现，Sparse-MLP 的感受野如图所示，有意思的点是：虽然在一层上看起来是十字形感受野，但是如果经过两个 Sparse-MLP 之后，其实能形成全局感受野！即如果该模块重复两次，每个 token 就可以聚合整个二维空间的信息。这个话之前 ViP，RaftMLP 等等这些没有提到哈，虽然他们也是一样的。

Sparse-MLP 实现代码如下所示：

import torch
from torch import nn

class sMLPBlock(nn.Module):
    def __init__(self,h=224,w=224,c=3):
        super().__init__()
        self.proj_h=nn.Linear(h,h)
        self.proj_w=nn.Linear(w,w)
        self.fuse=nn.Linear(3*c,c)
    
    def forward(self,x):
        x_h=self.proj_h(x.permute(0,1,3,2)).permute(0,1,3,2)
        x_w=self.proj_w(x)
        x_id=x
        x_fuse=torch.cat([x_h,x_w,x_id],dim=1)
        out=self.fuse(x_fuse.permute(0,2,3,1)).permute(0,3,1,2)
        return out


if __name__ == '__main__':
    input=torch.randn(50,3,224,224)
    smlp=sMLPBlock(h=224,w=224)
    out=smlp(input)
    print(out.shape)

2.3 计算复杂度

原文中是这样写的：

sMLP的复杂度为：$\Omega (sMLP)=HWC(H+W)+3HW{C}^2$，这其实很好理解，$HWCH$ 为 H 通道映射，$HWCW$ 为 W 通道映射，$3HW{C}^2$ 为融合后的线性降维映射。

相比而言，MLP-Mixer 的 token 混合部分的复杂度为：$\Omega (MLP)=2\alpha (HW{)}^{2}C$，其中 $\alpha$ 为第一个 MLP 节点扩展系数。

但是这样其实并不正确！sMLP 其实还包含了 $3\times 3$ DWConv，所以实际上的 sMLP 的复杂度为：$\Omega (sMLP)=HWC(H+W)+3HW{C}^2+9HWC$，

不过论文结论没有问题：可以看出，本文的方法将复杂度控制在了 $O(N\sqrt{N})$ 内，而 MLP-Mixer为 $O(N^2)$，其中 $N=HW$ 为 Token 的数量。这使得本文的方法可以处理更大的 $N$，并最终在金字塔结构中实现多阶段处理。

3. 消融实验

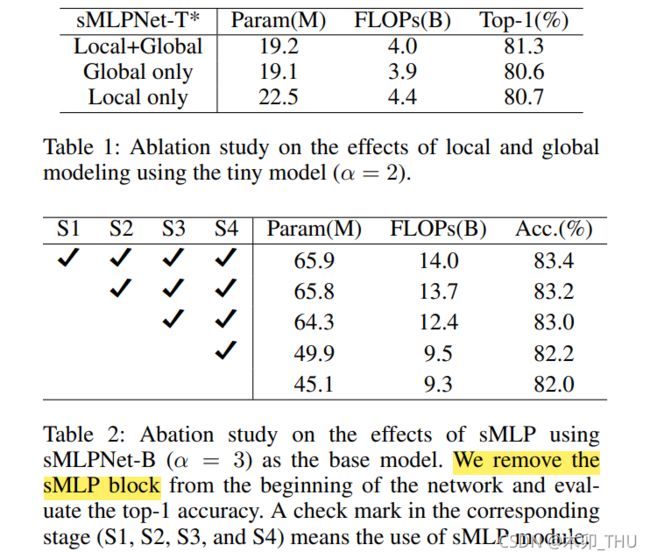
论文的消融实验主要讨论了以下四点：

• 局部感受野和全局感受野的性能如何？局部建模指 DWConv，全局建模指 Sparse-MLP 轴向线性映射。去掉局部建模之后，图像识别精度显著下降至80.6%。这表明，DWConv是一种非常有效的建模局部依赖关系的方法。去掉全局建模之后，图像识别精度显著下降至 80.7%，因此局部建模和全局建模在 sMLPNet 中都是重要的。这也反映了我之前的观点：如何更好地联合建模局部依赖和全局依赖是下一步前进的方向。此外，作者在不同阶段删除了 Sparse-MLP 轴向线性映射，结果如下表所示。所以看出，每个 stage 的 Sparse-MLP 全局依赖都是重要的。

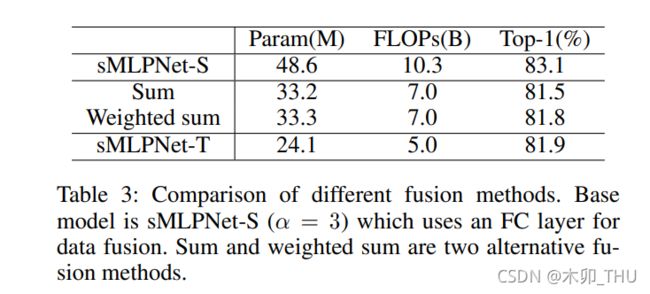
• 怎样进行特征融合比较好？Sparse-MLP 中特征融合方式：求和，加权求和（学习三个权重参数），通道拼接后使用 $1\times 1$ 卷积降维。最后发现还是使用 $1\times 1$ 卷积降维效果好。不过作者提到，性能的衰减可能因为求和以及加权求和方式的参数量低造成的，所以作者补了一个更小参数规模的 sMLPNet-T 作为参考。但是，Sparse-MLP 的加权求和方式较为简单，如果使用 ViP 以及 S2MLPv2 中使用的源自于 ResNeSt 的 Split-Attention 或许会更好。

• 三条分支需要有 Identity 分支吗？实验发现，确实需要！并且 horizontal processing, vertical processing 使用并行的效果比串行效果好，这与 ViP 的发现是一致的。所以 RaftMLP 的串行选择其实并不一定优异。

• 金字塔结构是不是更好？作者比较了单阶段和多阶段版本的 MLP 网络的性能，其中多阶段 MLP 其实就是将 sMLPNet 中的 token-mixing 替换回 MLP-Mixer 的，但是保留了金字塔结构。可以看出，多阶段版本可以达到更高的准确率。这个与 ViP 他们的发现也是一致的。

4. 反思与总结

本文从网络结构上而言没有特殊的开创性的贡献，不过已经能看到，stride = 1 或 2，这已经被学术界所关注到。本文大胆地说了我们用了 DWConv，而且本文行文很多词汇描述都值得学习，这点很不错。如果结合了 Split Attention 或许会更好，如果放出特征图进行分析可能会更好，如果现在开源则会更更好。

本工作有个问题在于：使用了轴向映射，这就使得网络需要依赖图像的长宽尺寸进行构建，那么这就使得网络对于图像分辨率敏感，无法用于后续下游任务，这也是诸多 MLP-based model 的通病。

5. 代码

我自己实现的非官方 pytorch 代码见 此处，其中 PatchMerging 函数取自 Swin Transformer 官方。

import torch
from torch import nn
from functools import partial
from einops.layers.torch import Rearrange, Reduce

def pair(val):
    return (val, val) if not isinstance(val, tuple) else val


class PreNormResidual(nn.Module):
    def __init__(self, dim, fn, norm = nn.LayerNorm):
        super().__init__()
        self.fn = fn
        self.norm = norm(dim)

    def forward(self, x):
        return self.fn(self.norm(x)) + x

class sMLPBlock(nn.Module):
    def __init__(self, h = 224, w = 224, d_model = 3):
        super().__init__()
        self.proj_h = nn.Linear(h, h)
        self.proj_w = nn.Linear(w, w)
        self.fuse = nn.Conv2d(3 * d_model, d_model, kernel_size = 1)
    
    def forward(self,x):
        x_h = self.proj_h(x.permute(0,1,3,2)).permute(0,1,3,2)
        x_w = self.proj_w(x)
        x_id = x
        x_fuse = torch.cat([x_h, x_w, x_id], dim=1)
        out = self.fuse(x_fuse)
        return out

class PatchMerging(nn.Module):
    r""" Patch Merging Layer.
    Args:
        input_resolution (tuple[int]): Resolution of input feature.
        dim (int): Number of input channels.
        norm_layer (nn.Module, optional): Normalization layer.  Default: nn.LayerNorm
    """

    def __init__(self, input_resolution, dim, norm_layer=nn.LayerNorm):
        super().__init__()
        self.input_resolution = input_resolution
        self.dim = dim
        self.reduction = nn.Linear(4 * dim, 2 * dim, bias=False)
        self.norm = norm_layer(4 * dim)

    def forward(self, x):
        """
        x: B, H*W, C
        """
        H, W = self.input_resolution
        B, H, W, C = x.shape
        assert H % 2 == 0 and W % 2 == 0, f"x size ({H}*{W}) are not even."

        x0 = x[:, 0::2, 0::2, :]  # B H/2 W/2 C
        x1 = x[:, 1::2, 0::2, :]  # B H/2 W/2 C
        x2 = x[:, 0::2, 1::2, :]  # B H/2 W/2 C
        x3 = x[:, 1::2, 1::2, :]  # B H/2 W/2 C
        x = torch.cat([x0, x1, x2, x3], -1)  # B H/2 W/2 4*C
        x = x.view(B, H // 2, W // 2, 4 * C)  # B H/2*W/2 4*C

        x = self.norm(x)
        x = self.reduction(x)

        return x

    def extra_repr(self) -> str:
        return f"input_resolution={self.input_resolution}, dim={self.dim}"

    def flops(self):
        H, W = self.input_resolution
        flops = H * W * self.dim
        flops += (H // 2) * (W // 2) * 4 * self.dim * 2 * self.dim
        return flops

class sMLPStage(nn.Module):
    def __init__(self, height, width, d_model, depth, expansion_factor = 2, dropout = 0., pooling = False):
        super().__init__()

        self.pooling = pooling
        self.patch_merge = nn.Sequential(
            Rearrange('b c h w -> b h w c'),
            PatchMerging((height, width), d_model),
            Rearrange('b h w c -> b c h w'),
        )

        self.model = nn.Sequential(
            *[nn.Sequential(
                PreNormResidual(d_model, nn.Sequential(
                    nn.Conv2d(d_model, d_model, kernel_size = 3, padding = 1, groups = d_model), 
                ), norm = nn.BatchNorm2d),
                PreNormResidual(d_model, nn.Sequential(
                    sMLPBlock(
                        height, width, d_model
                    )
                ), norm = nn.BatchNorm2d),
                Rearrange('b c h w -> b h w c'),
                PreNormResidual(d_model, nn.Sequential(
                    nn.Linear(d_model, d_model * expansion_factor),
                    nn.GELU(),
                    nn.Dropout(dropout),
                    nn.Linear(d_model * expansion_factor, d_model),
                    nn.Dropout(dropout),
                ), norm = nn.LayerNorm),
                Rearrange('b h w c -> b c h w'),
            ) for _ in range(depth)]
        )

    def forward(self, x):
        x = self.model(x)
        if self.pooling:
            x = self.patch_merge(x)
        return x


class SparseMLP(nn.Module):
    def __init__(
        self,
        image_size=224,
        patch_size=4,
        in_channels=3,
        num_classes=1000,
        d_model=96,
        depth=[2,10,24,2],
        expansion_factor = 2,
        patcher_norm = False,
    ):
        image_size = pair(image_size)
        patch_size = pair(patch_size)
        assert (image_size[0] % patch_size[0]) == 0, 'image must be divisible by patch size'
        assert (image_size[1] % patch_size[1]) == 0, 'image must be divisible by patch size'
        height = image_size[0] // patch_size[0]
        width = image_size[1] // patch_size[1]
        super().__init__()
        self.patcher = nn.Sequential(
            nn.Conv2d(in_channels, d_model, kernel_size=patch_size, stride=patch_size),

            nn.Identity() if (not patcher_norm) else nn.Sequential(
                Rearrange('b c h w -> b h w c'),
                nn.LayerNorm(d_model),
                Rearrange('b h w c -> b c h w'),
            )
        )

        self.layers = nn.ModuleList()
        for i_layer in range(len(depth)):
            i_depth = depth[i_layer]
            i_stage = sMLPStage(height // (2**i_layer), width // (2**i_layer), d_model, i_depth, expansion_factor = expansion_factor, pooling = ((i_layer + 1) < len(depth)))
            self.layers.append(i_stage)

            if (i_layer + 1) < len(depth):
                d_model = d_model * 2

        self.mlp_head = nn.Sequential(
            Rearrange('b c h w -> b h w c'),
            nn.LayerNorm(d_model),
            Reduce('b h w c -> b c', 'mean'),
            nn.Linear(d_model, num_classes)
        )

    def forward(self, x):
        i = 0
        embedding = self.patcher(x)
        for layer in self.layers:
            i += 1
            embedding = layer(embedding)
        out = self.mlp_head(embedding)
        return out