线性回归——波士顿放假预测

线性回归

线性回归核心思想：

利用最小二乘函数对一个或多个自变量之间关系进行建模的方法，预测回归问题。

优点：
    （1）思想简单，实现容易。建模迅速，对于小数据量、简单的关系很有效；
    （2）是许多强大的非线性模型的基础。
    （3）线性回归模型十分容易理解，结果具有很好的可解释性，有利于决策分析。
    （4）蕴含机器学习中的很多重要思想。
    （5）能解决回归问题。
缺点：
    （1）对于非线性数据或者数据特征间具有相关性多项式回归难以建模.
    （2）难以很好地表达高度复杂的数据。
 

---

正规方程

LinearRegression使用系数w =（w1，…，wp）拟合线性模型，以最小化数据集中实际目标值与通过线性逼近预测的目标之间的残差平方和。

API

class sklearn.linear_model.LinearRegression(fit_intercept=True)

    fit_intercept：是否计算偏置
    LinearRegression.coef_:回归系数
    LinearRegression.intercept_:偏置

正规方程——波士顿房价预测

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge
from sklearn.metrics import mean_squared_error
import joblib


"""
正规方程的优化方法对波士顿房价进行预测
:return:
"""
# 1）获取数据
boston = load_boston()

# 2）划分数据集
x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=7)

# 3）标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# 4）预估器
estimator = LinearRegression()
estimator.fit(x_train, y_train)

# 5）得出模型
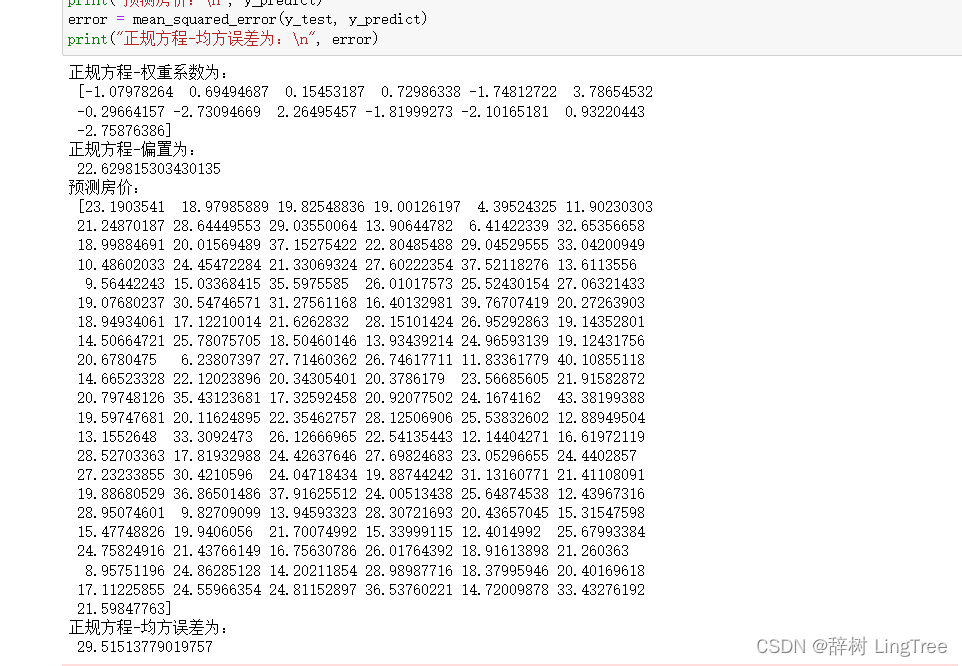
print("正规方程-权重系数为：\n", estimator.coef_)
print("正规方程-偏置为：\n", estimator.intercept_)

# 6）模型评估
y_predict = estimator.predict(x_test)
print("预测房价：\n", y_predict)
error = mean_squared_error(y_test, y_predict)
print("正规方程-均方误差为：\n", error)

 

---

梯度下降

API

sklearn.linear_model.SGDRegressor(loss="squared_loss", fit_intercept=True, learning_rate='invscaling', eta0=0.01)

    SGDRegressor类实现了随机梯度下降学习，它支持不同的loss函数和正则化惩罚项来拟合线性回归模型
    loss：损失类型
        loss='squared_loss'：普通最小二乘法
    fit_intercept:是否计算偏置
    learning_rate: string, optional
        学习率填充
        'constant': eta = eta0
        'optimal': eta = 1.0 / (alpha *(t + t0))[default]
        'invscaling': eta = eta0 / pow(t, power_t)
            power_t = 0.25 :存在父类当中
        对于一个常数值的学习率来说，可以使用learning_rate='constant'并使用eta0来指定学习率
    SGDRegressor.coef_:回归系数
    SGDRegressor.intercept_:偏置

梯度下降——波士顿房价预测

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge
from sklearn.metrics import mean_squared_error
import joblib

"""
梯度下降的优化方法对波士顿房价进行预测
:return:
"""
# 1）获取数据
boston = load_boston()
print("特征数量：\n", boston.data.shape)

# 2）划分数据集
x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)

# 3）标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# 4）预估器
estimator = SGDRegressor(learning_rate="constant", eta0=0.01, max_iter=10000, penalty="l1")
estimator.fit(x_train, y_train)

# 5）得出模型
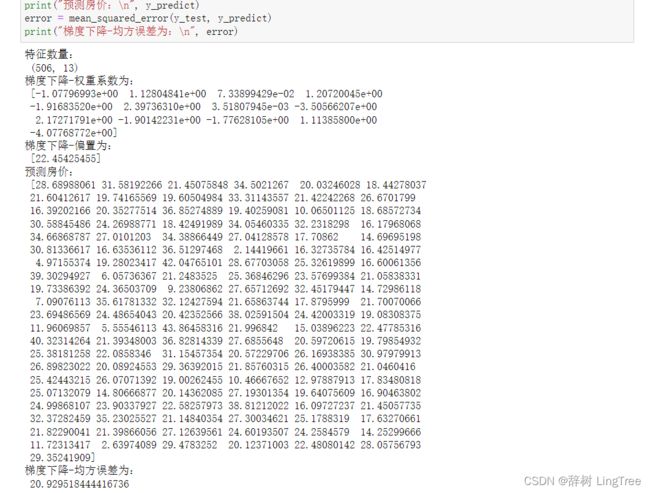
print("梯度下降-权重系数为：\n", estimator.coef_)
print("梯度下降-偏置为：\n", estimator.intercept_)

# 6）模型评估
y_predict = estimator.predict(x_test)
print("预测房价：\n", y_predict)
error = mean_squared_error(y_test, y_predict)
print("梯度下降-均方误差为：\n", error)

 

---

岭回归

岭回归核心思想：

带有L2正则化的线性回归，达到了解决过拟合的效果。

API

sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True, solver="auto", normalize=False)
    
    具有L2正则化的线性回归
    alpha: 正则化力度
        取值：0~1， 1~10
    solver: 会根据数据自动选择优化方法
        sag: 如果数据集、特征都比较大，选择该随机梯度下降优化
    normalize: 数据是否进行标准化
        normalize=False：可以在fit之前调用preprocessing.StandardScaler标准化数据
    Ridge.coef_: 回归权重
    Ridge.intercept_：回归偏置

sklearn.linear_model.RidgeCV(_BaseRidgeCV, RegressorMixin)

    具有L2正则化的线性回归，可以进行交叉验证
    coef_: 回归系数

岭回归——波士顿房价预测

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge
from sklearn.metrics import mean_squared_error
import joblib

"""
岭回归对波士顿房价进行预测
:return:
"""
# 1）获取数据
boston = load_boston()
print("特征数量：\n", boston.data.shape)

# 2）划分数据集
x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)

# 3）标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# 4）预估器
estimator = Ridge(alpha=0.5, max_iter=10000)
estimator.fit(x_train, y_train)



# 5）得出模型
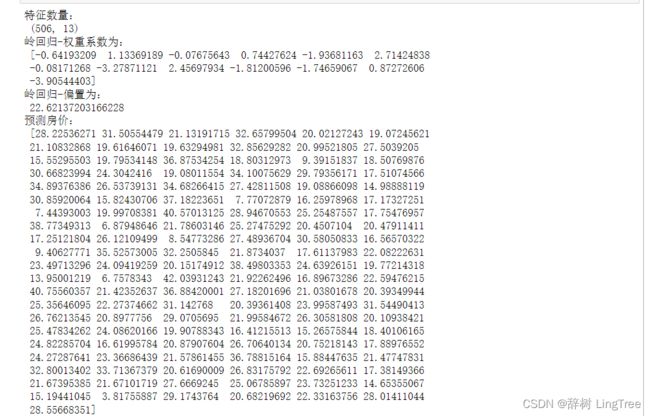
print("岭回归-权重系数为：\n", estimator.coef_)
print("岭回归-偏置为：\n", estimator.intercept_)

# 6）模型评估
y_predict = estimator.predict(x_test)
print("预测房价：\n", y_predict)
error = mean_squared_error(y_test, y_predict)