特征工程(六)—(1)利用PCA进行特征转换
(1)鸢尾花数据集的手动处理
PCA利用了协方差矩阵的特征值分解
过程如下:
(1)创建数据集的协方差矩阵
(2)计算协方差矩阵的特征值
(3)保留前K个特征值(按照特征值降序排列)
(4)要保留的特征向量转换新的数据点
1、加载鸢尾花数据集
import matplotlib as mpl
# 解决中文乱码
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
# 从sklearn中导入鸢尾花数据集
from sklearn.datasets import load_iris
# 导入画图模块
import matplotlib.pyplot as plt
%matplotlib inline
# (1)、加载数据集
iris = load_iris()
# (2)、将数据矩阵和相应变量存储到iris_x和iris_y中
iris_X, iris_y = iris.data, iris.target
print('要预测的花的名字:', iris.target_names)
print('预测的特征名称:', iris.feature_names)
要预测的花的名字: ['setosa' 'versicolor' 'virginica']
预测的特征名称: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
label_dict = {i : k for i,k in enumerate(iris.target_names)}
print(label_dict)
{0: 'setosa', 1: 'versicolor', 2: 'virginica'}
# 定义函数,画出其中两个特征的散点图
def plot(X, y, title, x_label, y_label):
ax = plt.subplot(111)
for label,market,color in zip(range(3),('^', 's' , 'o'), ('blue', 'red', 'green')):
plt.scatter(
x=X[:, 0].real[y == label],
y = X[:, 1].real[y == label],
color=color,
alpha=0.5,
label=label_dict[label]
)
plt.xlabel(x_label)
plt.ylabel(y_label)
leg = plt.legend(loc='upper right', fancybox=True)
leg.get_frame().set_alpha(0.5)
plt.title(title)
plot(iris_X, iris_y, 'original iris data', 'sepal length (cm)', 'sepal width (cm)')
2、手动PCA处理
1、创建数据集的协方差矩阵
# 然后在数据集上执行PCA
# 第一步、创建数据集的协方差矩阵
import numpy as np
# 计算均值向量
mean_vector = iris_X.mean(axis=0)
print('均值向量: ',mean_vector)
# 计算协方差矩阵
cov_mat = np.cov((iris_X).T)
print('协方差矩阵: ', cov_mat)
2、计算协方差矩阵的特征值
# 第二步、计算协方差矩阵的特征值
# 计算鸢尾花数据集的特征向量和特征值
eig_val_cov, eig_vec_cov = np.linalg.eig(cov_mat)
# 按照降序打印特征向量和相应的特征值
for i in range(len(eig_val_cov)):
eigvec_cov = eig_vec_cov[:, i]
print('Eigenvector {}: \n{}'.format(i + 1, eigvec_cov))
print('Eigvenvalue {} from 特征矩阵: {}'.format(i + 1,eig_val_cov[i]))
print(30 * '-')
3、保留前K个特征值(按照特征值降序排列)
# 第三步、按照降序保留前K个特征值
# 使用碎石图,显示每个主成分解释数据总方差的百分比
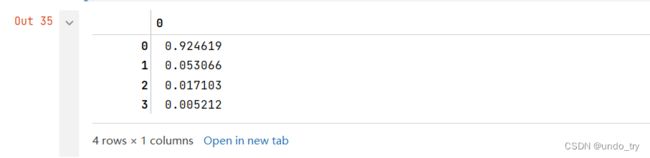
explained_variance_ratio = eig_val_cov / eig_val_cov.sum()
# 可以看出,4个主成分解释的部分有很大的差异,第一个主成分可以解释方差的92%以上
explained_variance_ratio
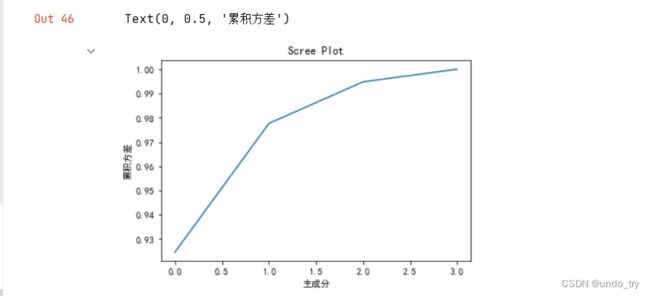
# 利用碎石图进行可视化
plt.plot(np.cumsum(explained_variance_ratio))
plt.title('Scree Plot')
plt.xlabel('主成分')
plt.ylabel('累积方差')
4、要保留的特征向量转换新的数据点
# 从图中可以看出,前两个主成分占据了原始方差的98%,意味着可以只用前两个特征向量作为新的主成分
# 这样将数据集缩小了一半,而且保持了特征的完整性,加速了性能
# 第四步、使用保留的特征向量转换新的数据点
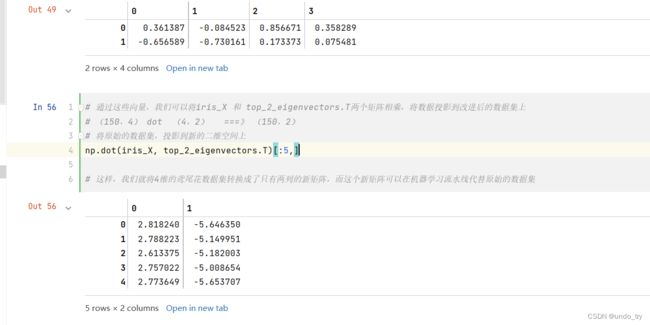
# 保存两个特征向量
top_2_eigenvectors = eig_vec_cov[:, :2].T
# 转置,每行是一个主成分,两行代表两个主成分
top_2_eigenvectors
(2)scikit-learn中PCA
# 从scikit-learn的分解模块导入
from sklearn.decomposition import PCA
import numpy as np
import matplotlib as mpl
# 解决中文乱码
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
# 从sklearn中导入鸢尾花数据集
from sklearn.datasets import load_iris
# 导入画图模块
import matplotlib.pyplot as plt
%matplotlib inline
# (1)、加载鸢尾花数据集
iris = load_iris()
# (2)、将数据矩阵和相应变量存储到iris_x和iris_y中
iris_X, iris_y = iris.data, iris.target
# 实例化有2个组件的PCA对象
pca = PCA(n_components=2)
# 拟合数据
pca.fit(iris_X)
# 查看pca的属性components_和 手动计算的top_2_eigenvectors 是否匹配
print(pca.components_)
# 可以看到第二个主成分是之前计算值的负数,不过在这没有问题,因为这两个特征都有效,而且也是不相关的
label_dict = {i : k for i,k in enumerate(iris.target_names)}
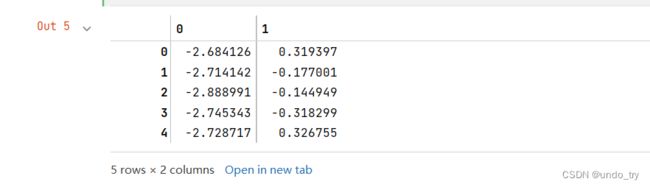
# 将数据投影到新的二维平面上
pca.transform(iris_X)[:5,]
# 结果和手动计算的不同,因为scikit-learn中的pca会在预测阶段将数据中心化,从而改变结果
'''
中心化和缩放对PCA的影响:
为什么不在计算特征向量就进行中心化操作,这是因为,原始矩阵和中心化后矩阵的协方差矩阵相同,因此它们的特征值分解也相同.因此,scikit-learn
的PCA不会对数据进行中心化,因为无论是否进行中心化操作,结果都一样.
缩放是指对数据进行中心化,并且除以标准差.
缩放后,与中心化的主成分不同,解释方差的百分比会比之前低得多,因为数据进行缩放后,列和列的协方差会更加一致,而不是集中在一个主成分中.
'''
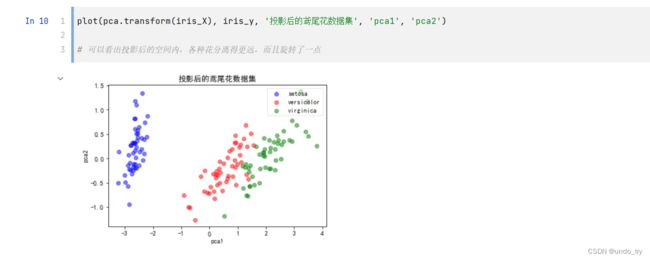
# 绘制鸢尾花数据集,比较投影前和投影后的样子
# 定义函数,画出其中两个特征的散点图
def plot(X, y, title, x_label, y_label):
ax = plt.subplot(111)
for label,market,color in zip(range(3),('^', 's' , 'o'), ('blue', 'red', 'green')):
plt.scatter(
x=X[:, 0].real[y == label],
y = X[:, 1].real[y == label],
color=color,
alpha=0.5,
label=label_dict[label]
)
plt.xlabel(x_label)
plt.ylabel(y_label)
leg = plt.legend(loc='upper right', fancybox=True)
leg.get_frame().set_alpha(0.5)
plt.title(title)
# 提取每个主成分解释的方差量
pca.explained_variance_ratio_
# pca主要优点之一:消除相关特征
# 本质上,特征值分解时候,得到所有的主成分都互相垂直,意思是批次线性无关
# 很多机器学习模型假设输入的特征是相互独立的,因此消除相关特征的好处很大,我们可以利用pca来确保这一点