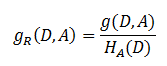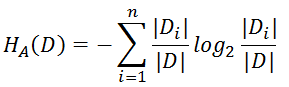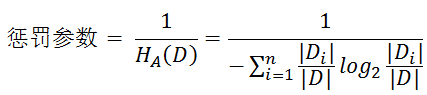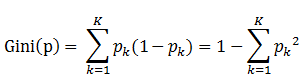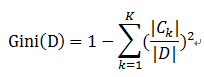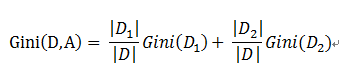机器学习之决策树算法的原理流程以及实现
1.决策树
决策树是附加概率结果的一个树状的决策图,是直观的运用统计概率分析的图法。机器学习中决策树是一个预测模型,它表示对象属性和对象值之间的一种映射,树中的每一个节点表示对象属性的判断条件,其分支表示符合节点条件的对象。树的叶子节点表示对象所属的预测结果。
![]()
1.1 信息增益
定义: 以某特征划分数据集前后的熵的差值
在熵的理解那部分提到了,熵可以表示样本集合的不确定性,熵越大,样本的不确定性就越大。因此可以使用划分前后集合熵的差值来衡量使用当前特征对于样本集合D划分效果的好坏。
划分前样本集合D的熵是一定的 ,entroy(前),
使用某个特征A划分数据集D,计算划分后的数据子集的熵 entroy(后)
信息增益 = entroy(前) - entroy(后)
书中公式:
做法:计算使用所有特征划分数据集D,得到多个特征划分数据集D的信息增益,从这些信息增益中选择最大的,因而当前结点的划分特征便是使信息增益最大的划分所使用的特征。
信息增益的理解:
对于待划分的数据集D,其 entroy(前)是一定的,但是划分之后的熵 entroy(后)是不定的,entroy(后)越小说明使用此特征划分得到的子集的不确定性越小(也就是纯度越高),因此 entroy(前) - entroy(后)差异越大,说明使用当前特征划分数据集D的话,其纯度上升的更快。而我们在构建最优的决策树的时候总希望能更快速到达纯度更高的集合,这一点可以参考优化算法中的梯度下降算法,每一步沿着负梯度方法最小化损失函数的原因就是负梯度方向是函数值减小最快的方向。同理:在决策树构建的过程中我们总是希望集合往最快到达纯度更高的子集合方向发展,因此我们总是选择使得信息增益最大的特征来划分当前数据集D。
缺点:信息增益偏向取值较多的特征
原因:当特征的取值较多时,根据此特征划分更容易得到纯度更高的子集,因此划分之后的熵更低,由于划分前的熵是一定的,因此信息增益更大,因此信息增益比较 偏向取值较多的特征
实现代码
def chooseBestFeatureToSplit(dataSet): # 选择信息增益最大的特征
numFeatures = len(dataSet[0]) - 1
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0
bestFeature = -1
for i in range(numFeatures):
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
newEntropy = 0.0
for value in uniqueVals:
subdataSet = splitdataSet(dataSet, i, value)
prob = len(subdataSet) / float(len(dataSet))
newEntropy += prob * calcShannonEnt(subdataSet)
infoGain = baseEntropy - newEntropy
if infoGain > bestInfoGain:
bestInfoGain = infoGain
bestFeature = i
return bestFeature
运行结果
1.2 信息增益率
信息增益比 = 惩罚参数 * 信息增益
书中公式:
注意:其中的H A(D),对于样本集合D,将当前特征A作为随机变量(取值是特征A的各个特征值),求得的经验熵。
(之前是把集合类别作为随机变量,现在把某个特征作为随机变量,按照此特征的特征取值对集合D进行划分,计算熵HA(D))
信息增益比本质: 是在信息增益的基础之上乘上一个惩罚参数。特征个数较多时,惩罚参数较小;特征个数较少时,惩罚参数较大。
惩罚参数:数据集D以特征A作为随机变量的熵的倒数,即:将特征A取值相同的样本划分到同一个子集中(之前所说数据集的熵是依据类别进行划分的)
缺点:信息增益比偏向取值较少的特征
原因: 当特征取值较少时H A(D)的值较小,因此其倒数较大,因而信息增益比较大。因而偏向取值较少的特征。
使用信息增益比:基于以上缺点, 并不是直接选择信息增益率最大的特征,而是现在候选特征中找出信息增益高于平均水平的特征,然后在这些特征中再选择信息增益率最高的特征。
实现代码
def chooseBestFeatureToSplit(dataSet): # 选择信息增益最大的特征
numFeatures = len(dataSet[0]) - 1
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0
bestFeature = -1
for i in range(numFeatures):
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
newEntropy = 0.0
for value in uniqueVals:
subdataSet = splitdataSet(dataSet, i, value)
prob = len(subdataSet) / float(len(dataSet))
newEntropy += prob * calcShannonEnt(subdataSet)
infoGain = baseEntropy - newEntropy
if infoGain > bestInfoGain:
bestInfoGain = infoGain
bestFeature = i
return bestFeature
运行结果
1.3 基尼指数
原理
定义:基尼指数(基尼不纯度):表示在样本集合中一个随机选中的样本被分错的概率。
注意: Gini指数越小表示集合中被选中的样本被分错的概率越小,也就是说集合的纯度越高,反之,集合越不纯。
即 基尼指数(基尼不纯度)= 样本被选中的概率 * 样本被分错的概率
书中公式:
说明:
1. pk表示选中的样本属于k类别的概率,则这个样本被分错的概率是(1-pk)
2. 样本集合中有K个类别,一个随机选中的样本可以属于这k个类别中的任意一个,因而对类别就加和
3. 当为二分类是,Gini(P) = 2p(1-p)
样本集合D的Gini指数 : 假设集合中有K个类别,则:
基于特征A划分样本集合D之后的基尼指数:
需要说明的是CART是个二叉树,也就是当使用某个特征划分样本集合只有两个集合:1. 等于给定的特征值 的样本集合D1 , 2 不等于给定的特征值 的样本集合D2
实际上是对拥有多个取值的特征的二值处理。
举个例子:
假设现在有特征 “学历”,此特征有三个特征取值: “本科”,“硕士”, “博士”,
当使用“学历”这个特征对样本集合D进行划分时,划分值分别有三个,因而有三种划分的可能集合,划分后的子集如下:
-
- 划分点: “本科”,划分后的子集合 : {本科},{硕士,博士}
- 划分点: “硕士”,划分后的子集合 : {硕士},{本科,博士}
- 划分点: “硕士”,划分后的子集合 : {博士},{本科,硕士}
对于上述的每一种划分,都可以计算出基于 划分特征= 某个特征值 将样本集合D划分为两个子集的纯度:
因而对于一个具有多个取值(超过2个)的特征,需要计算以每一个取值作为划分点,对样本D划分之后子集的纯度Gini(D,Ai),(其中Ai 表示特征A的可能取值)
然后从所有的可能划分的Gini(D,Ai)中找出Gini指数最小的划分,这个划分的划分点,便是使用特征A对样本集合D进行划分的最佳划分点。
实现代码
def calcProbabilityEnt(dataSet):
numEntries = len(dataSet)
feaCounts = 0
fea1 = dataSet[0][len(dataSet[0])-1]
for feaVec in dataSet:
if feaVec[-1] == fea1:
feaCounts += 1
probabilityEnt = float(feaCounts) / numEntries
return probabilityEnt
#选择最好的数据集划分方式
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1 #特征数量,numfeature为特征的维度,因为最后一列为标签,所以需要减去1
if numFeatures == 1:
return 0
bestGini = 1 #最佳基尼指数
bestFeature = -1 #最优的划分特征初始化为-1
for i in range(numFeatures): #遍历所有的特征
featList = [example[i] for example in dataSet]
feaGini = 0 #定义特征的值的基尼系数
uniqueVals = set(featList)
for value in uniqueVals: #遍历该特征维度下对应的所有特征值
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet)/float(len(dataSet))
probabilityEnt = calcProbabilityEnt(subDataSet)
feaGini += prob * (2 * probabilityEnt * (1 - probabilityEnt))
if (feaGini < bestGini):
bestGini = feaGini
bestFeature = i #记录基尼指数最小的索引值
return bestFeature
运行结果
1.4 我的数据集
1.5 全段代码
from math import log, pow
import operator
import matplotlib.pyplot as plt
def calcShannonEnt(dataSet): # 计算香农熵
numEntries = len(dataSet)
labelCounts = {}
for featVec in dataSet:
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key]) / numEntries
shannonEnt -= prob * log(prob, 2)
return shannonEnt
def splitdataSet(dataSet, axis, value): # 分类数据
retdataSet = []
for featVec in dataSet:
if featVec[axis] == value:
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis + 1:])
retdataSet.append(reducedFeatVec)
return retdataSet
def countProb(subdataSet): #计算基尼指数
num=len(subdataSet)
featCount=0
feat=subdataSet[0][-1]
for i in subdataSet:
if i[-1]==feat:
featCount+=1
prob=float(featCount)/num
return prob
def GiniIndex(dataSet): # 计算以特征A为分割的最小基尼指数
dataSetLen=len(dataSet)
numFeatures = len(dataSet[0]) - 1
bestGini = 1.0 # 初始基尼指数
bestFeature = -1
for i in range(numFeatures):
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
giniSplit=0.0
for value in uniqueVals:
subdataSet = splitdataSet(dataSet, i, value)
prob=countProb(subdataSet) # 计算p值
featSplit=featList.count(value)
newGiniPercent=float(featSplit)/dataSetLen # 计算该value的占比
giniSplit+=newGiniPercent*2*prob*(1-prob)
if giniSplit < bestGini:
bestGini = giniSplit
bestFeature = i
return bestFeature
def majorityCnt(classList): # 多数决决定分类
classCount = {}
for vote in classList:
if vote not in classCount.keys():
classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
def createTree(dataSet, labels): # 生成字典形式的树
classList = [example[-1] for example in dataSet]
if classList.count(classList[0]) == len(classList):
return classList[0]
if len(dataSet[0]) == 1:
return majorityCnt(classList)
# bestFeat = chooseBestFeatureToSplit(dataSet) # 信息增益
# bestFeat = GainRatio(dataSet) # 信息增益率
bestFeat = GiniIndex(dataSet) # 基尼指数,无论那种分类标准,都是更改bestFeat
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel: {}}
del (labels[bestFeat])
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
subLabels = labels[:]
myTree[bestFeatLabel][value] = createTree(splitdataSet(dataSet, bestFeat, value), subLabels)
return myTree
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")
def getNumLeafs(myTree):
numLeafs = 0
# firstStr = myTree.keys()[0] 2.7的语法,3.6不适用
firstSides = list(myTree.keys())
firstStr = firstSides[0] # 找到输入的第一个元素
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[
key]).__name__ == 'dict': # test to see if the nodes are dictonaires, if not they are leaf nodes
numLeafs += getNumLeafs(secondDict[key])
else:
numLeafs += 1
return numLeafs
def getTreeDepth(myTree):
maxDepth = 1
firstSides = list(myTree.keys())
firstStr = firstSides[0] # 找到输入的第一个元素
# firstStr = myTree.keys()[0] #注意这里和机器学习实战中代码不同,这里使用的是Python3,而在Python2中可以写成这种形式
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]) == dict:
thisDepth = 1 + getTreeDepth(secondDict[key])
else:
thisDepth = 1
if thisDepth > maxDepth: maxDepth = thisDepth
return maxDepth
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
xytext=centerPt, textcoords='axes fraction',
va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)
def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]
yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
def plotTree(myTree, parentPt, nodeTxt):
numLeafs = getNumLeafs(myTree)
depth = getTreeDepth(myTree)
firstSides = list(myTree.keys())
firstStr = firstSides[0] # 找到输入的第一个元素
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff)
plotMidText(cntrPt, parentPt, nodeTxt)
plotNode(firstStr, cntrPt, parentPt, decisionNode)
secondDict = myTree[firstStr]
plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict':
plotTree(secondDict[key], cntrPt, str(key))
else:
plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD
def createPlot(inTree):
fig = plt.figure(1, facecolor='white')
fig.clf()
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) # no ticks
# createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
plotTree.totalW = float(getNumLeafs(inTree))
plotTree.totalD = float(getTreeDepth(inTree))
plotTree.xOff = -0.5 / plotTree.totalW
plotTree.yOff = 1.0
plotTree(inTree, (0.5, 1.0), '')
plt.show()
def classify(inputTree, featLabels, testVec): # 决策树执行分类
firstStr = list(inputTree.keys())[0]
secondDict = inputTree[firstStr]
# print(secondDict)
featIndex = featLabels.index(firstStr)
try:
for key in secondDict.keys():
if testVec[featIndex] == key: # 查找测试样本中是否有标签与决策树中的相同
if type(secondDict[key]).__name__ == "dict":
classLabels = classify(secondDict[key], featLabels, testVec)
else:
classLabels = secondDict[key]
return classLabels
except:
if type(secondDict[key]).__name__ == "str":
return secondDict[key]
else:
return classify(secondDict[key], featLabels, testVec) # 如果树并未走到叶子节点就异常终止,则递归调用函数对其子节点进行决策
def file_train(filename): # 取数据集偶数作为训练集
fr = open(filename)
lines = fr.readlines()
# print(lines)
res = []
i = 0
for line in lines:
line = line.strip()
temp = line.split(",")
if i % 2 == 0: # 取总数据集里的偶数
res.append(temp)
i += 1
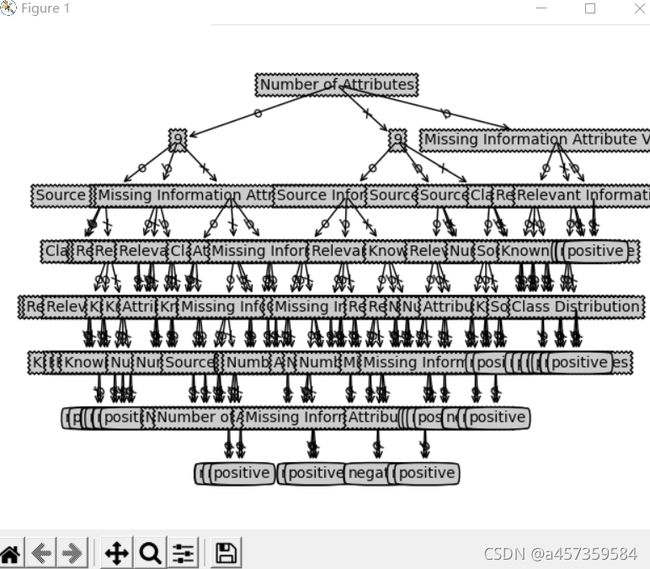
labels = ["Source Information", "Known Past Usage", "Relevant Information", "Number of Information", "Number of Attributes","Attribute Information","Missing Information Attribute Values","Class Distribution","9"]
return res, labels
def file_test(filename): # 取数据集的奇数作为测试集
fr = open(filename)
lines = fr.readlines()
# print(lines)
res = []
i = 0
for line in lines:
line = line.strip()
temp = line.split(",")
if i % 2 == 1: # 取总数据集里的奇数
res.append(temp)
i += 1
labels = [ "Source Information", "Known Past Usage", "Relevant Information", "Number of Information", "Number of Attributes","Attribute Information","Missing Information Attribute Values","Class Distribution","9"]
return res, labels
def getAnswer(filename): # 获得真实的答案
fr = open(filename)
lines = fr.readlines()
i = 0
storage = []
for it in lines:
it = it.strip()
temp = it.split(",")
if i % 2 == 1:
storage.append(temp[-1])
i += 1
return storage
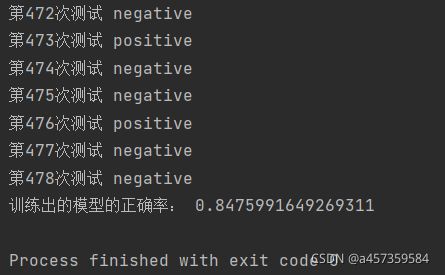
def test1():
# 训练模型
dataSet, labels = file_train("tic-tac-toe.txt")
labelsBackup = labels[:]
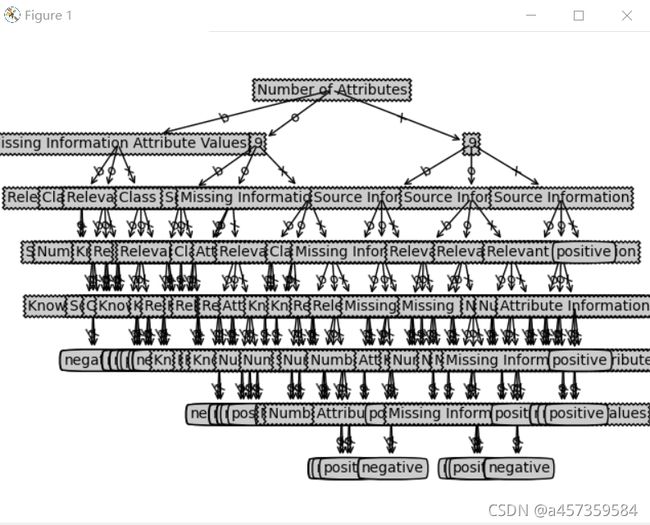
tree = createTree(dataSet, labels)
createPlot(tree)
dataSet_test, labels_test = file_test("tic-tac-toe.txt")
labels_testBackup = labels_test
j = 0
resTest = []
for item in dataSet_test:
testAns = classify(tree, labels_testBackup, item)
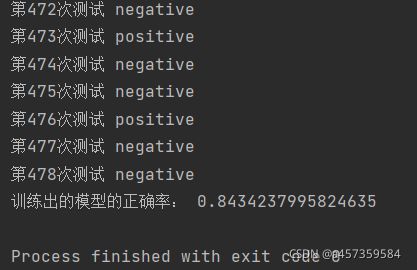
print("第%d次测试" % j, testAns)
resTest.append(testAns)
j += 1
aList = getAnswer("tic-tac-toe.txt")
count = 0
for x in range(len(aList)):
if resTest[x] == aList[x]:
count += 1
print("训练出的模型的正确率:", count / len(aList))
if __name__ == '__main__':
test1()
理论上来说应该是基尼指数的精度会是最高的,但是这边不知道哪里出了问题我的信息增益率方法训练效果最好
2.总结
ID3和C4.5算法均只适合在小规模数据集上使用(实际上CART也是小规模,只不过规模会相对大一些)
ID3和C4.5、CART算法都是单变量决策树
当属性值取值比较多的时候,最好考虑C4.5算法,ID3得出的效果会比较差
决策树分类一般情况只适合小数据量的情况(数据可以放内存,因为计算概率,数据得都加载)
CART算法是三种算法中最常用的一种决策树构建算法。
三种算法的区别仅仅只是对于当前树的评价标准不同而已,ID3使用信息增益、C4.5使用信息增益率、CART使用基尼系数或均方差。