强化学习: Policy Gradient

---

---

前言

按照目前的发展方向，强化学习大致可分为value-based，policy-based，以及两者的结合体actor-critic这三种体系。其中，DeepMind主要采用的是value-based，OpenAI主要采用的是policy-based（RL两大流派的历史渊源见此处）。由于目前需要用到policy gradient，因此先对这部分进行学习。

---

参考资料

知乎：https://zhuanlan.zhihu.com/p/107906954
李宏毅：http://speech.ee.ntu.edu.tw/~tlkagk/courses_MLDS18.html（本文图片均来源于该强化课程的课件）
pytorch：https://github.com/pytorch/examples/tree/main/reinforcement_learning

---

一、算法原理

1. 回合(episode)与轨迹（trajectory）

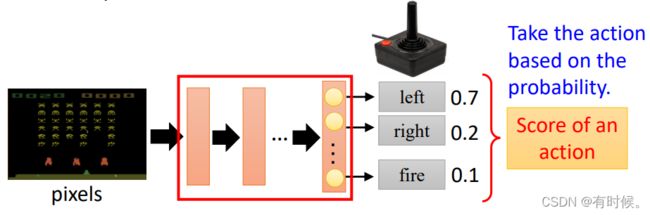
对于一个控制飞机射击外星人的游戏，如果通过神经网络输出动作概率来控制飞机的行动，如向左移动、向右移动和开火，以此来获取最高的游戏分数，那么这个神经网络就是策略网络（Policy Network）。

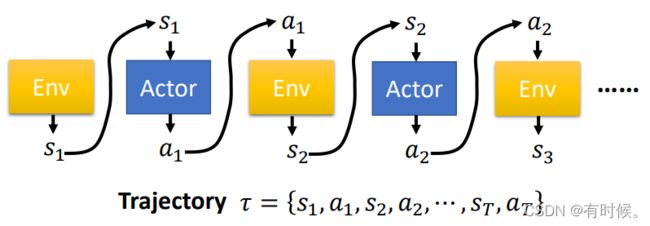
在一个游戏回合（episode）中，由在时间上连续的状态（state）和动作（action）所构成的序列叫做轨迹（trajectory）。显然，一个游戏回合内只有一条轨迹（具有随机性）。策略网络要做的就是接收状态state并输出该状态下各个action的概率。
一条轨迹发生的概率$p_{\theta }(\tau )$可以按照下式计算：
$p_{\theta }(\tau )$
$=p(s_1)p_{\theta }(a_1|s_1)p(s_2|s_1,a_1)p_{\theta }(a_2|s_2)p(s_3|s_2,a_2)\cdot \cdot \cdot p_{\theta }(a_t|s_t)p(s_{t+1}|s_t,a_t)\cdot \cdot \cdot$
$=p(s_1)\prod _{t=1}^T{p}_{\theta }(a_t|s_t)p(s_{t+1}|s_t,a_t)$
其中，只有$p_{\theta }(a_t|s_t)$这一项与网络参数$\theta$有关，表示在状态$s_t$下选择动作$a_t$的概率。

2. 奖励（reward）与损失函数

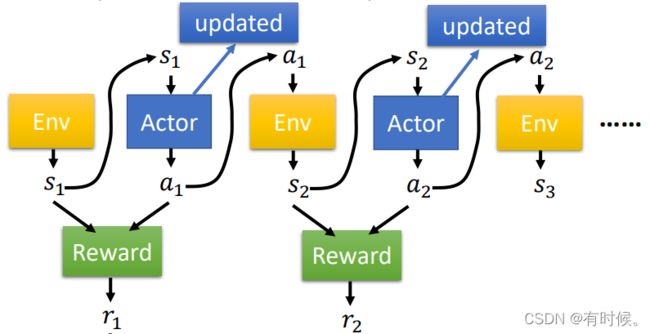
一条轨迹的总reward为$R(\tau )=\sum _t{r}_t$，在训练策略网络时要采样多条轨迹，则期望reward为：$$\overline{R_{\theta }}=\sum _{\tau }R(\tau )p_{\theta }(\tau )={\mathbb{E}}_{\tau \sim p_{\theta }(\tau )}[R(\tau )]$$强化学习的目标为：求得最优参数$\theta$，使得$\overline{R_{\theta }}$最大：
$${\theta }^{\ast }=arg\underset{\theta }{\max }\overline{R_{\theta }}=arg\underset{\theta }{\max }{\mathbb{E}}_{\tau \sim p_{\theta }(\tau )}[R(\tau )]$$由于强化学习中不存在标签，因此就将$\overline{R_{\theta }}$作为损失函数。

3. 策略梯度（Policy Gradient）

确定损失函数后，需要采用梯度优化方法来更新策略网络参数$\theta$，由于目标是使$\overline{R_{\theta }}$最大，因此采用梯度上升法。
$\nabla \overline{R_{\theta }}$
$=\sum _{\tau }R(\tau )\nabla p_{\theta }(\tau )$
$=\sum _{\tau }R(\tau )p_{\theta }(\tau )\nabla log{p}_{\theta }(\tau )$
$={\mathbb{E}}_{\tau \sim p_{\theta }}[R(\tau )\nabla log{p}_{\theta }(\tau )]$
$\approx \frac{1}{n}\sum _{n=1}^{N}R({\tau }^n)\nabla log{p}_{\theta }({\tau }^n)$
$=\frac{1}{n}\sum _{n=1}^N\sum _{t=1}^{T^n}R({\tau }^n)\nabla log{p}_{\theta }(a_t^n|s_t^n)$

① 第一个等式到第二个等式用到了一个技巧：$\nabla f(x)=f(x)\nabla logf(x)$
② 倒数第二个等式的意思是通过采样的方式来近似计算期望，$N$表示采样的轨迹数量；
③ 最后一个等式中$T^n$表示在第$n$条轨迹中包含$T$个step。
$$\theta =\theta +\eta \nabla \overline{R_{\theta }}$$然后通过梯度上升法更新参数。

---

二、Tips

1. baseline

由第一部分可知：$\nabla \overline{R_{\theta }}=\frac{1}{n}\sum _{n=1}^N\sum _{t=1}^{T^n}R({\tau }^n)\nabla log{p}_{\theta }(a_t^n|s_t^n)$，观察该式会发现，对于一条轨迹中的每个step选择动作的概率，对应的权重都是一条轨迹的总reward，在reward总是正的情况下，意味着在第t个step时所有动作被选择的概率都要上升。在理想状况下，所有动作都会被采样到，即便reward都是正的，不同大小的reward经过normalize后，大的reward对应的动作概率会上升，反之，小的会下降。

但是在实际情况中，往往有动作不会被采样到（特别是一个回合更新一次参数，且一个回合内step较少时），由于所有动作被选择的概率和为1，此时就会出现没有被采样到的动作概率减小的问题，即使该动作是最优的，这样很可能会错过最优解。

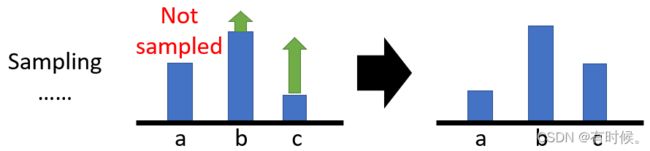
解决这个问题的方式就是让reward有正有负，在原式的基础上减去一个baseline即可：
$$\nabla \overline{R_{\theta }}=\frac{1}{n}\sum _{n=1}^N\sum _{t=1}^{T^n}(R({\tau }^n)-b)\nabla log{p}_{\theta }(a_t^n|s_t^n)$$baseline通常由network输出，此处不深究。

2. 分配合理权重 & 折扣回报

再次观察该式，$\nabla \overline{R_{\theta }}=\frac{1}{n}\sum _{n=1}^N\sum _{t=1}^{T^n}R({\tau }^n)\nabla log{p}_{\theta }(a_t^n|s_t^n)$，一条轨迹中每个step选择动作概率的权重都是$R({\tau }^n)$，这显然是不太合理的。首先，一条轨迹得到了比较好的reward，不代表每个step选择的action都是好的；其次，对于第$t$个step，所选择的动作只会影响未来的reward。因此，需要对每个step选择的action分配合理的权重，才能反映这个action对总的reward实际的贡献。
$$\nabla \overline{R_{\theta }}=\frac{1}{n}\sum _{n=1}^N\sum _{t=1}^{T^n}{U}_t\nabla log{p}_{\theta }(a_t^n|s_t^n)$$$$U_t=\sum _{t^{\prime }=t}^{T^n}{r}_{t^{\prime }}^n$$更进一步，考虑到随着step的增大，当前step选择的action对于未来的影响会越来越小，则有：$$U_t=\sum _{t^{\prime }=t}^{T^n}{\gamma }^{t^{\prime }-t}{r}_{t^{\prime }}^n$$

---

三、pytorch实现

参考pytorch官方提供的例子：

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.distributions import Categorical

import numpy as np
import argparse
import gym


def args():
    parser = argparse.ArgumentParser(description='PyTorch REINFORCE example')
    parser.add_argument('--gamma', type=float, default=0.99, metavar='G',
                        help='discount factor (default: 0.99)')
    parser.add_argument('--seed', type=int, default=1314, metavar='N',
                        help='random seed (default: 1314)')
    parser.add_argument('--render', action='store_true',
                        help='render the environment')
    parser.add_argument('--episodes', type=int, default=1000, metavar='N',
                        help='number of episodes for training agent(default: 1000)')
    parser.add_argument('--steps', type=int, default=1000, metavar='N',
                        help='number of steps per episode (default: 1000)')
    parser.add_argument('--lr', type=float, default=1e-2,
                        help='learning rate')
    parser.add_argument('--log-interval', type=int, default=10, metavar='N',
                        help='interval between training status logs (default: 10)')
    return parser.parse_args()


class Policy(nn.Module):
    def __init__(self, obs_n, act_n, hidden_size):
        super(Policy, self).__init__()
        num_outputs = act_n

        self.linear1 = nn.Linear(obs_n, hidden_size)
        self.dropout = nn.Dropout(p=0.6)
        self.linear2 = nn.Linear(hidden_size, num_outputs)

    def forward(self, x):
        x = self.linear1(x)
        x = self.dropout(x)
        x = F.relu(x)
        actions_scores = self.linear2(x)
        return F.softmax(actions_scores, dim=1)


class ReinforceAgent(object):
    def __init__(self, policy, lr, gamma):
        super(ReinforceAgent, self).__init__()
        self.policy = policy
        self.optimizer = torch.optim.Adam(self.policy.parameters(), lr=lr)
        self.gamma = gamma
        self.saved_log_probs = []
        self.rewards = []

    def select_action(self, state):
        state = torch.from_numpy(state).float().unsqueeze(0)
        probs = self.policy(state)
        action_distributions = Categorical(probs)
        action = action_distributions.sample()
        log_probs = action_distributions.log_prob(action)
        self.saved_log_probs.append(log_probs)
        return action.item()

    def learn(self):
        eps = np.finfo(np.float32).eps.item()
        policy_loss = []
        R = 0
        returns = []
        # calculate discount rewards
        for r in self.rewards[::-1]:
            R = r + self.gamma * R
            returns.insert(0, R)
        returns = torch.tensor(returns)
        returns = (returns - returns.mean()) / (returns.std() + eps)
        for log_prob, reward in zip(self.saved_log_probs, returns):
            policy_loss.append(-log_prob*reward)
        policy_loss = torch.cat(policy_loss).sum()
        self.optimizer.zero_grad()
        policy_loss.backward()
        self.optimizer.step()

        del self.saved_log_probs[:]
        del self.rewards[:]


def train_agent(args):
    env = gym.make('CartPole-v1')
    policy = Policy(obs_n=env.observation_space.shape[0], act_n=env.action_space.n, hidden_size=128)
    agent = ReinforceAgent(policy, lr=args.lr, gamma=args.gamma)

    env.reset(seed=args.seed)
    torch.manual_seed(args.seed)

    running_reward = 10
    for i_episode in range(args.episodes):
        state, ep_reward = env.reset(), 0
        for step in range(args.steps):
            action = agent.select_action(state)
            state, reward, done, _ = env.step(action)
            if args.render:
                env.render()
            agent.rewards.append(reward)
            ep_reward += reward
            if done:
                break

        running_reward = 0.05 * ep_reward + (1 - 0.05) * running_reward
        agent.learn()
        if i_episode % args.log_interval == 0:
            print('Episode {}\tLast reward: {:.2f}\tAverage reward: {:.2f}'.format(
                i_episode, ep_reward, running_reward))
        if running_reward > env.spec.reward_threshold:
            print("Solved! Running reward is now {} and "
                  "the last episode runs to {} time steps!".format(running_reward, step))
            break


if __name__ == '__main__':
    args = args()
    train_agent(args)

一共做了四组实验：
① 分配合理权重（gamma=1.0）
② 使用discount reward（gamma=0.99）
③ 使用一条轨迹的总reward作为权重（total reward）
④ 在total reward的基础上减去baseline
每组实验均训练1000个episode，最大step为1000，结果如下：

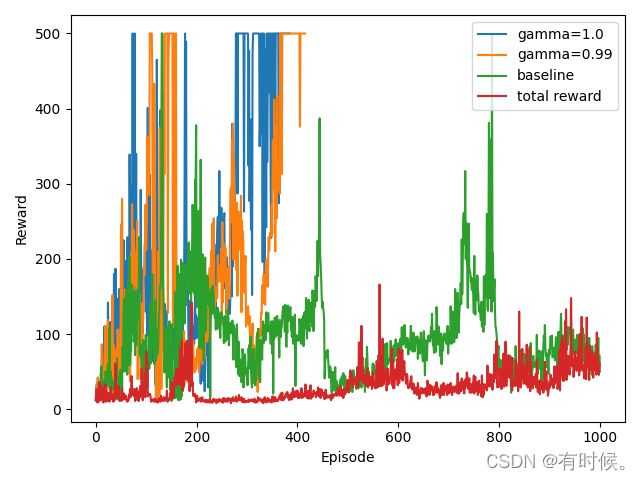
从图中可以看出：
① 当为每个step选择动作的概率分配合理的权重时（gamma=1.0 or 0.99），网络会快速收敛。反之，每个step分配相同的权重时网络很难收敛。
② 分配合理权重时，是否使用折扣回报在该任务中影响不大，不使用反而会收敛更快。因此，在自己的任务中需要根据实验结果来选择是否使用折扣回报。
③ 添加一个常数baseline效果比不添加好。（使用network来输出一个可以学习的baseline可能取得比较好的效果）

附上测试代码：

import torch
import torch.nn as nn
import torch.nn.functional as F
import gym
from torch.distributions import Categorical

class Policy(nn.Module):
    def __init__(self):
        super(Policy, self).__init__()
        self.affine1 = nn.Linear(4, 128)
        self.dropout = nn.Dropout(p=0.6)
        self.affine2 = nn.Linear(128, 2)

        self.saved_log_probs = []
        self.rewards = []

    def forward(self, x):
        x = self.affine1(x)
        x = self.dropout(x)
        x = F.relu(x)
        action_scores = self.affine2(x)
        return F.softmax(action_scores, dim=1)

def select_action(policy, state):
    state = torch.from_numpy(state).float().unsqueeze(0)
    probs = policy(state)
    m = Categorical(probs)
    action = m.sample()
    policy.saved_log_probs.append(m.log_prob(action))
    return action.item()

def main():
    policy = Policy()
    policy.load_state_dict(torch.load('./checkpoint/[email protected]'))
    policy.eval()

    env = gym.make('CartPole-v1')
    state = env.reset()

    for t in range(1000):
        env.render()
        action = select_action(policy, state)
        state, reward, done, _ = env.step(action)

        if done:
            break

    env.close()

if __name__ == '__main__':
    main()

效果：