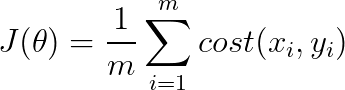word2vec原理详解及实战

目录

1）前言

1.1 语言模型

1.2N-gram模型

1.3词向量表示

2）预备知识

2.1 sigmoid函数

2.2 逻辑回归

2.3贝叶斯公式

2.4 Huffman编码

3）神经网络概率语言模型

4）基于Hierarchial Sodtmax模型

4.1CBOW模型

4.2 Skip-gram模型

5）基于Negative Sampling的模型

5.1如何选取负样本

5.2 CBOW模型

5.3 Skip-gram模型

6）基于TensorFlow的word2vec实战

参考资料：

---

---

---

本章主要介绍了word2vec中的数学原理及基于TensorFlow的实现。

1）前言

word2vec是Google在2013年开源推出的有个用于获取word vector的工具包，它简单，高效，因此引起了很多人关注。它是一个很简单的浅层结构，今天就来揭开的面纱。

从官方的介绍可以看出word2vec是一个将词表示为一个向量的工具，通过该向量表示，可以用来进行更深入的自然语言处理，比如机器翻译等。

为了理解word2vec的设计思想，我们有必要先学习一下自然语言处理的相关发展历程和基础知识。

1.1 语言模型

• 语言模型其实就是看一句话是不是正常人说出来的。这玩意很有用，比如机器翻译、语音识别得到若干候选之后，可以利用语言模型挑一个尽量靠谱的结果。在 NLP 的其它任务里也都能用到。
• 用数学表达的话，就是给定T个词w1,w2,...wT，看它是自然语言的概率P，公式如下所示：

• 举例来说，比如一段语音识别为“我喜欢吃梨”和“我喜欢吃力”，根据分词和上述公式，可以得到两种表述的概率计算分别为下面的公式，而其中每一个子项的概率我们可以事先通过大量的语料统计得到，这样我们就可以得到更好的识别效果。

P('我喜欢吃梨') = P('我') * P('喜欢'|'我') * P('吃'|'我','喜欢') * P('梨'|'我','喜欢','吃')
P('我喜欢吃力') = P('我') * P('喜欢'|'我') * P('吃力'|'我','喜欢')

1.2N-gram模型

• 通过上面的语言模型计算的例子，大家可以发现，如果一个句子比较长，那么它的计算量会很大；
• 牛逼的科学家们想出了一个N-gram模型来简化计算，在计算某一项的概率时Context不是考虑前面所有的词，而是前N-1个词；
• 当然牛逼的科学家们还在此模型上继续优化，比如N-pos模型从语法的角度出发，先对词进行词性标注分类，在此基础上来计算模型的概率；后面还有一些针对性的语言模型改进，这里就不一一介绍。
• 通过上面简短的语言模型介绍，我们可以看出核心的计算在于P(wi|Contenti)，对于其的计算主要有两种思路：一种是基于统计的思路，另外一种是通过函数拟合的思路；前者比较容易理解但是实际运用的时候有一些问题（比如如果组合在语料里没出现导致对应的条件概率变为0等），而函数拟合的思路就是通过语料的输入训练出一个函数P(wi|Contexti) = f(wi,Contexti;θ)，这样对于测试数据就直接套用函数计算概率即可，这也是机器学习中惯用的思路之一。

1.3词向量表示

• 自然语言理解的问题要转化为机器学习的问题，第一步肯定是要找一种方法把这些符号数学化。
• 最直观的就是把每个词表示为一个很长的向量。这个向量的维度是词表的大小，其中绝大多数元素为0，只有一个维度的值为1，这个维度就代表了当前的词。这种表示方式被称为One-hot Representation。这种方式的优点在于简洁，但是却无法描述词与词之间的关系。
• 另外一种表示方法是通过一个低维的向量（通常为50维、100维或200维），其基于“具有相似上下文的词，应该具有相似的语义”的假说，这种表示方式被称为Distributed Representation。它是一个稠密、低维的实数向量，它的每一维表示词语的一个潜在特征，该特征捕获了有用的句法和语义特征。其特点是将词语的不同句法和语义特征分布到它的每一个维度上去表示。这种方式的好处是可以通过空间距离或者余弦夹角来描述词与词之间的相似性。
• 以下我们来举个例子看看两者的区别：

// One-hot Representation 向量的维度是词表的大小，比如有10w个词，该向量的维度就是10w
v('足球') = [0 1 0 0 0 0 0 ......]
v('篮球') = [0 0 0 0 0 1 0 ......]

// Distributed Representation 向量的维度是某个具体的值如50
v('足球') = [0.26 0.49 -0.54 -0.08 0.16 0.76 0.33 ......]
v('篮球') = [0.31 0.54 -0.48 -0.01 0.28 0.94 0.38 ......]

 

2）预备知识

这里介绍一下后面用到的知识点，包括sigmoid函数，逻辑回归，贝叶斯公式，Huffman树等。

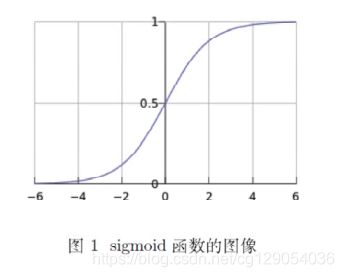
2.1 sigmoid函数

sigmoid函数是神经网络常用的激活函数，定义为：

图像为：

导数形式为：

此时我们可以得到以下结论：

， 

2.2 逻辑回归

逻辑回归是我们第一个学习到的机器学习算法，这里只介绍逻辑回归的整体损失函数。

其中代价函数为：

2.3贝叶斯公式

这里也直接给出贝叶斯公式：

2.4 Huffman编码

这里简单介绍霍夫曼树的构造：给定n个权值作为二叉树的n个叶子结点，可通过如下算法来构造。

1）将看成是n棵树的森林（每棵树仅有一个节点）；

2）在森林中选出两个根节点的权值最小的树合并，作为一颗新树的左右子树，且新树的根节点权值为其左右子树根节点权值之和。

3）从森林中删除选取的两棵树，并将新树加入森林。

4）重复（2）（3）步，直到森林中只剩一棵树为止，该树即为所求的霍夫曼树。

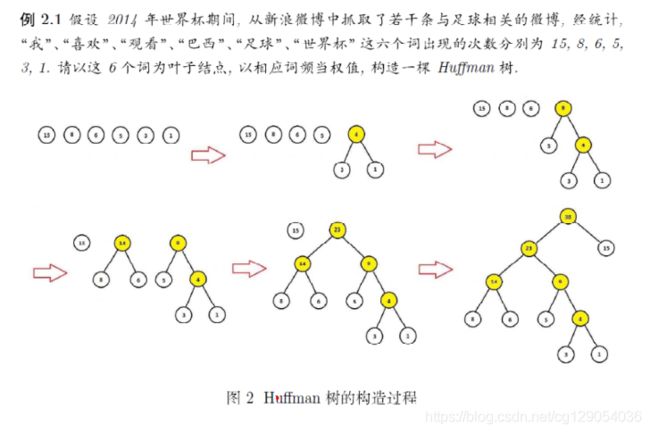
下面是一个例子：

下面是霍夫曼编码示意图：

3）神经网络概率语言模型

• 神经网络概率语言模型（NNLM）把词向量作为输入（初始的词向量是随机值），训练语言模型的同时也在训练词向量，最终可以同时得到语言模型和词向量。
• Bengio等牛逼的科学家们用了一个三层的神经网络来构建语言模型，同样也是N-gram 模型。 网络的第一层是输入层，是上下文的N-1个向量组成的(n-1)m维向量；第二层是隐藏层，使用tanh作为激活函数；第三层是输出层，每个节点表示一个词的未归一化概率，最后使用softmax激活函数将输出值归一化。

• 得到这个模型，然后就可以利用梯度下降法把模型优化出来，最终得到语言模型和词向量表示。

4）基于Hierarchial Sodtmax模型

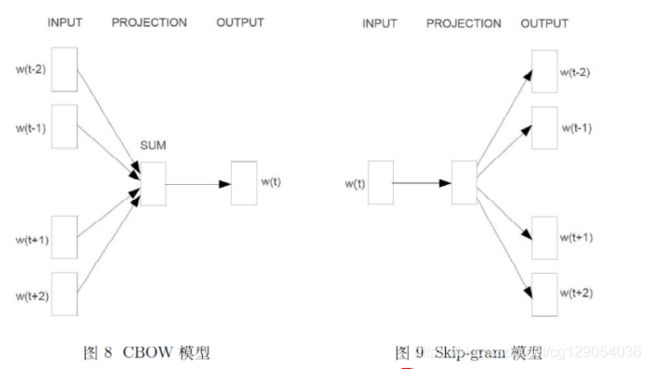
现在开始正式介绍word2vec中用到的两个重要模型----CBOW模型和Skip-pram模型。下面是两个模型的示意图，两个模型都包含输入层、投影层、输出层。前者是在已知当前词的上下文的前提下预测当前词；后者恰恰相反，是在已知当前词的前提下预测上下文。

对于这两个模型，word2vec给出了两套框架，现在介绍基于Hierarchical Softmax的CBOW和Skip-gram模型。

4.1CBOW模型

CBOW模型全名为Continuous bags of words。之所以叫bags-of-words是因为输入层到投影层的操作由『拼接』变成了『叠加』，对于『叠加而言』，无所谓词的顺序，所以称为词袋模型。

• 上下文：由w前后各c个词构成
• 输入层：包含2c个词的词向量
• 投影层：输入层的2c个词做『累加求和』。

• 输出层：输出层对应的是一棵Huffman树。该Huffman树以语料中出现的词为叶子节点，以各词在语料中出现的次数当做权值构造出来的。该树中，叶子节点总共有N个。

对比CBOW模型结构和神经概率语言模型的模型结构，区别在于：

• 输入层到投影层：CBOW是『累加』，神经概率语言是『拼接』
• 隐藏层：CBOW无隐藏层，神经概率语言有
• 输出层：CBOW是『树形结构』，神经概率语言是『线性结构』

4.2 Skip-gram模型

Skip-gram模型是已知当前词w，对其上下文中的词进行预测。

 

网络结构：

• 输入层：当前样本的中心词w的词向量
• 投影层：其实没什么作用
• 输出层：类似CBOW模型，也是一颗Huffman树

5）基于Negative Sampling的模型

5.1如何选取负样本

选取负样本需要按照一定的概率分布，Word2vec的作者们测试发现最佳的分布是3/4次幂的Unigram distribution。

来它认为语料库中所有的词出现的概率都是互相独立的。所以就是按照在语料库中随机选择，因此高频词被选中的概率大，低频词被选中的概率小，这也很符合逻辑。概率分布公式如下： 

5.2 CBOW模型

5.3 Skip-gram模型

6）基于TensorFlow的word2vec实战

""" Word2Vec.
Implement Word2Vec algorithm to compute vector representations of words.
This example is using a small chunk of Wikipedia articles to train from.
References:
    - Mikolov, Tomas et al. "Efficient Estimation of Word Representations
    in Vector Space.", 2013.
Links:
    - [Word2Vec] https://arxiv.org/pdf/1301.3781.pdf
Author: Aymeric Damien
Project: https://github.com/aymericdamien/TensorFlow-Examples/
"""
from __future__ import division, print_function, absolute_import

import collections
import os
import random
import urllib
import zipfile

import numpy as np
import tensorflow as tf

# Training Parameters
learning_rate = 0.1
batch_size = 128
num_steps = 3000000
display_step = 10000
eval_step = 200000

# Evaluation Parameters
eval_words = ['five', 'of', 'going', 'hardware', 'american', 'britain']

# Word2Vec Parameters
embedding_size = 200 # Dimension of the embedding vector
max_vocabulary_size = 50000 # Total number of different words in the vocabulary
min_occurrence = 10 # Remove all words that does not appears at least n times
skip_window = 3 # How many words to consider left and right
num_skips = 2 # How many times to reuse an input to generate a label
num_sampled = 64 # Number of negative examples to sample


# Download a small chunk of Wikipedia articles collection
url = 'http://mattmahoney.net/dc/text8.zip'
data_path = 'text8.zip'
if not os.path.exists(data_path):
    print("Downloading the dataset... (It may take some time)")
    filename, _ = urllib.urlretrieve(url, data_path)
    print("Done!")
# Unzip the dataset file. Text has already been processed
with zipfile.ZipFile(data_path) as f:
    text_words = f.read(f.namelist()[0]).lower().split()

# Build the dictionary and replace rare words with UNK token
count = [('UNK', -1)]
# Retrieve the most common words
count.extend(collections.Counter(text_words).most_common(max_vocabulary_size - 1))
# Remove samples with less than 'min_occurrence' occurrences
for i in range(len(count) - 1, -1, -1):
    if count[i][1] < min_occurrence:
        count.pop(i)
    else:
        # The collection is ordered, so stop when 'min_occurrence' is reached
        break
# Compute the vocabulary size
vocabulary_size = len(count)
# Assign an id to each word
word2id = dict()
for i, (word, _)in enumerate(count):
    word2id[word] = i

data = list()
unk_count = 0
for word in text_words:
    # Retrieve a word id, or assign it index 0 ('UNK') if not in dictionary
    index = word2id.get(word, 0)
    if index == 0:
        unk_count += 1
    data.append(index)
count[0] = ('UNK', unk_count)
id2word = dict(zip(word2id.values(), word2id.keys()))

print("Words count:", len(text_words))
print("Unique words:", len(set(text_words)))
print("Vocabulary size:", vocabulary_size)
print("Most common words:", count[:10])

data_index = 0
# Generate training batch for the skip-gram model
def next_batch(batch_size, num_skips, skip_window):
    global data_index
    assert batch_size % num_skips == 0
    assert num_skips <= 2 * skip_window
    batch = np.ndarray(shape=(batch_size), dtype=np.int32)
    labels = np.ndarray(shape=(batch_size, 1), dtype=np.int32)
    # get window size (words left and right + current one)
    span = 2 * skip_window + 1
    buffer = collections.deque(maxlen=span)
    if data_index + span > len(data):
        data_index = 0
    buffer.extend(data[data_index:data_index + span])
    data_index += span
    for i in range(batch_size // num_skips):
        context_words = [w for w in range(span) if w != skip_window]
        words_to_use = random.sample(context_words, num_skips)
        for j, context_word in enumerate(words_to_use):
            batch[i * num_skips + j] = buffer[skip_window]
            labels[i * num_skips + j, 0] = buffer[context_word]
        if data_index == len(data):
            buffer.extend(data[0:span])
            data_index = span
        else:
            buffer.append(data[data_index])
            data_index += 1
    # Backtrack a little bit to avoid skipping words in the end of a batch
    data_index = (data_index + len(data) - span) % len(data)
    return batch, labels


# Input data
X = tf.placeholder(tf.int32, shape=[None])
# Input label
Y = tf.placeholder(tf.int32, shape=[None, 1])

# Ensure the following ops & var are assigned on CPU
# (some ops are not compatible on GPU)
with tf.device('/cpu:0'):
    # Create the embedding variable (each row represent a word embedding vector)
    embedding = tf.Variable(tf.random_normal([vocabulary_size, embedding_size]))
    # Lookup the corresponding embedding vectors for each sample in X
    X_embed = tf.nn.embedding_lookup(embedding, X)

    # Construct the variables for the NCE loss
    nce_weights = tf.Variable(tf.random_normal([vocabulary_size, embedding_size]))
    nce_biases = tf.Variable(tf.zeros([vocabulary_size]))

# Compute the average NCE loss for the batch
loss_op = tf.reduce_mean(
    tf.nn.nce_loss(weights=nce_weights,
                   biases=nce_biases,
                   labels=Y,
                   inputs=X_embed,
                   num_sampled=num_sampled,
                   num_classes=vocabulary_size))

# Define the optimizer
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
train_op = optimizer.minimize(loss_op)

# Evaluation
# Compute the cosine similarity between input data embedding and every embedding vectors
X_embed_norm = X_embed / tf.sqrt(tf.reduce_sum(tf.square(X_embed)))
embedding_norm = embedding / tf.sqrt(tf.reduce_sum(tf.square(embedding), 1, keepdims=True))
cosine_sim_op = tf.matmul(X_embed_norm, embedding_norm, transpose_b=True)

# Initialize the variables (i.e. assign their default value)
init = tf.global_variables_initializer()

with tf.Session() as sess:

    # Run the initializer
    sess.run(init)

    # Testing data
    x_test = np.array([word2id[w] for w in eval_words])

    average_loss = 0
    for step in xrange(1, num_steps + 1):
        # Get a new batch of data
        batch_x, batch_y = next_batch(batch_size, num_skips, skip_window)
        # Run training op
        _, loss = sess.run([train_op, loss_op], feed_dict={X: batch_x, Y: batch_y})
        average_loss += loss

        if step % display_step == 0 or step == 1:
            if step > 1:
                average_loss /= display_step
            print("Step " + str(step) + ", Average Loss= " + \
                  "{:.4f}".format(average_loss))
            average_loss = 0

        # Evaluation
        if step % eval_step == 0 or step == 1:
            print("Evaluation...")
            sim = sess.run(cosine_sim_op, feed_dict={X: x_test})
            for i in xrange(len(eval_words)):
                top_k = 8  # number of nearest neighbors
                nearest = (-sim[i, :]).argsort()[1:top_k + 1]
                log_str = '"%s" nearest neighbors:' % eval_words[i]
                for k in xrange(top_k):
                    log_str = '%s %s,' % (log_str, id2word[nearest[k]])
                print(log_str)

参考资料：

https://github.com/aymericdamien/TensorFlow-Examples/blob/master/examples/2_BasicModels/word2vec.py

https://blog.csdn.net/itplus/article/details/37969979

https://blog.csdn.net/mytestmy/article/details/26969149

https://www.jianshu.com/p/418f27df3968

http://www.hankcs.com/nlp/word2vec.html