ICLR 21可信多视图分类论文笔记:Trusted Multi-view Classification
TRUSTED MULTI-VIEW CLASSIFICATION
1、方法动机
-
多视图数据一般指多源数据,包括多模态数据、多传感器数据、不同方法所提取的数据特征等等。利用多视图数据之间的互补性往往能够增强算法的性能表现。
-
在多视图学习中,一般的算法通常认为每个视图的数据是“平等”的。这种固定权重的方式实际上有一个潜在的假设:所有样本的各个视图的质量都保持稳定。然而在实际上,不同样本的不同视图的质量完全可能不同,因此,模型应该对此能够有适应性的变化。
-
在某些场景中,比如医疗场景,对于模型给出的预测,我们不仅要知道预测结果,还要知道预测的置信度以及为什么拥有这样高\低的置信度。这要求模型能够对最终决策结果、甚至是每个视图的决策给出一个准确的不确定度。
2、本文方法
①获得证据——非负神经网络
②③意见生成—主观逻辑(subjective logic)通过将输入建模为狄利克雷分布来获得不同类的分配概率和不确定性。
④多源融合——Dempster-Shafer证据融合理论
-
传统方法(上图右图)使用softmax作为输出层,使用softmax输出作为预测的置信度,往往会导致高置信度,即使是错误的预测(输出概率和为一,即使不属于任何一类)
-
如上图左图所示,作者引入了一种evidence-base的不确定性估计技术主观逻辑(subjective logic)SL通过将输入建模为狄利克雷分布来获得不同类的分配概率和不确定性。它可以提供更准确的不确定性,并使我们能够灵活地集成多个视图来进行可信决策
2.1 获得证据——非负神经网络
对应Figure 1的①。
- Evidence指从输入中收集到的支持分类的度量。
- 获取 Evidence:
去掉单视图分类模型的softmax层,替换成一般的非负输出的激活层(ReLU)。
确保网络输出非负值,这些值被认为是证据向量。因此,可以获得狄利克雷分布的参数。
2.2意见生成
对应Figure 1的②③。
主观逻辑(Subjective logic)能够基于从数据中收集的证据,用狄利克雷分布进行建模,获取多分类问题的各类概率(belief mass)和总体不确定度(uncertainty mass)。
SL将狄利克雷分布的参数与evidence联系起来。
2.2.1 狄利克雷分布
如图所示, θ \theta θ是随机变量,它的限制是 Σ k θ k = 1 , θ k ≥ 0 \Sigma_k \theta_k=1, \theta_k \geq 0 Σkθk=1,θk≥0, 参数 α \alpha α的大小会影响随机变量 θ \theta θ的行为。 α ≥ 0 \alpha \geq 0 α≥0且 θ \theta θ和 α \alpha α都是K维向量。
当K=3时,3维的狄利克雷分布的支撑集是3维空间内顶点(0,0,1)(0,1,0)(1,0,0)的等边三角形(标准2-单形)
单纯形是三角形和四面体的一种泛化,一个 n 维单纯形是指包含 (n+1)个节点的凸多面体。
可看成三类,等边三角形的三个角分别属于三个类,红色代表随机变量在此处分布非常密集。比如第一行第二列中α=[0.2,0.2,0.2],随机变量会聚集在三个端点上。
传统神经网络的输出可以视为单纯性上的一个点,而狄利克雷分布为整个单纯形上每个点赋予了概率密度。Figure 2.5密度图,第一幅可以对应于α=[0.2,0.2,0.2]的情形,第二幅可以对应于α=[1,1,1],第三幅可以对应于α=[5,5,5]。
2.2.2 本文做法
定义狄利克雷分布参数为: α k v = e k v + 1 α_k^v=e_k^v+1 αkv=ekv+1
将狄利克雷分布的参数与证据联系起来。

对于每个视图的分类模型,都能够给出一个分类概率的狄利克雷分布。
狄利克雷分布为整个单纯形上每个点赋予了概率密度。
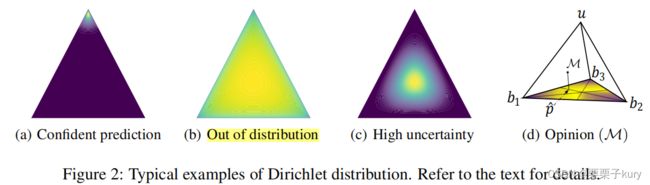
- (a) e=<40,1,1>,以标准2-单形顶部为中心的尖锐分布。表明已经观察到足够的证据来确保准确的分类
- (b) e=<0.0001, 0.0001, 0.0001>表示分类证据很少,u≈1
- © 每个证据都很高,不确定性变高(尽管总体上的不确定性较(b)降低
- (d) 基于主观逻辑 (Eq. 1 and Eq. 2),将一个狄利克雷分布转化为一个标准3-单形(在R^4有顶点(1,0,0,0),(0,1,0,0),(0,0,1,0)(0,0,0,1)的正四面体)
对于每个视图,称 M v = { { b k v } k = 1 K , u v } M^v=\{\{b^v_k\}^K_{k=1},u^v\} Mv={{bkv}k=1K,uv}为视图v的subjective Opinion。相应地,狄利克雷分布的期望值p是M在底部的投影。 p ^ k v = α k v S v \hat p^v_k=\frac{α^v_k}{S^v} p^kv=Svαkv,v表示第v个视图,K表示K分类。
2.3多源融合——Dempster-Shafer证据融合理论
对应Figure 1的④。
举个例子,要根据view1和view2的观点融合出判断为树的概率。首先要找与“判断为树”交集不为空的mass,然后两两乘积求和
m f i x ( b t r e e m a s s ) = 1 1 − k [ m 1 ( b t r e e m a s s ) ∗ m 2 ( b t r e e m a s s ) + m 1 ( b t r e e m a s s ) ∗ m 2 ( u ) + m 1 ( u ) ∗ m 2 ( b t r e e m a s s ) ] = 1 1 − k ∗ ( 0.27 ∗ 0.1 + 0.27 ∗ 0.8 + 0.1 ∗ 0.1 ) m_{fix}(b_{tree} mass)=\frac1{1−k}[m_1(b_{tree} mass)∗m_2(b_{tree} mass)+m_1(b_{tree} mass)∗m_2(u)+m_1(u)∗m_2(b_{tree} mass)]=\frac1{1−k}*(0.27*0.1+0.27*0.8+0.1*0.1) mfix(btreemass)=1−k1[m1(btreemass)∗m2(btreemass)+m1(btreemass)∗m2(u)+m1(u)∗m2(btreemass)]=1−k1∗(0.27∗0.1+0.27∗0.8+0.1∗0.1)
k描述冲突程度。
k = m 1 ( b t r e e m a s s ) ∗ m 2 ( b c a r m a s s ) + m 1 ( b t r e e m a s s ) ∗ m 2 ( b p e r s o n m a s s ) + m 1 ( b c a r m a s s ) ∗ m 2 ( b p e r s o n m a s s ) + m 2 ( b t r e e m a s s ) ∗ m 1 ( b c a r m a s s ) + m 2 ( b t r e e m a s s ) ∗ m 2 ( b p e r s o n m a s s ) + . . . = 0.27 ∗ 0.06 + 0.27 ∗ 0.04 + 0.27 ∗ 0.04 + 0.1 ∗ 0.27 + 0.1 ∗ 0.36 + . . . k=m_1(b_{tree} mass)∗m_2(b_{car} mass)+m_1(b_{tree} mass)∗m_2(b_{person} mass)+m_1(b_{car} mass)∗m_2(b_{person} mass)+m_2(b_{tree} mass)∗m_1(b_{car} mass)+m_2(b_{tree} mass)∗m_2(b_{person} mass)+...=0.27*0.06+0.27*0.04+0.27*0.04+0.1*0.27+0.1*0.36+... k=m1(btreemass)∗m2(bcarmass)+m1(btreemass)∗m2(bpersonmass)+m1(bcarmass)∗m2(bpersonmass)+m2(btreemass)∗m1(bcarmass)+m2(btreemass)∗m2(bpersonmass)+...=0.27∗0.06+0.27∗0.04+0.27∗0.04+0.1∗0.27+0.1∗0.36+...
本文的做法就是如此,它设计了简化。
此时u和 b k b_k bk已知,可以求出 e k e_k ek和α。有了α,能得出最终融合出来的狄利克雷分布,再根据最下方公式得到各类的最终概率 b k b_k bk和总体不确定性u。(因为要求它们的和为一,之前那个直接融合出来的 b k b_k bk和u不满足)
2.4 Learning to form opinion
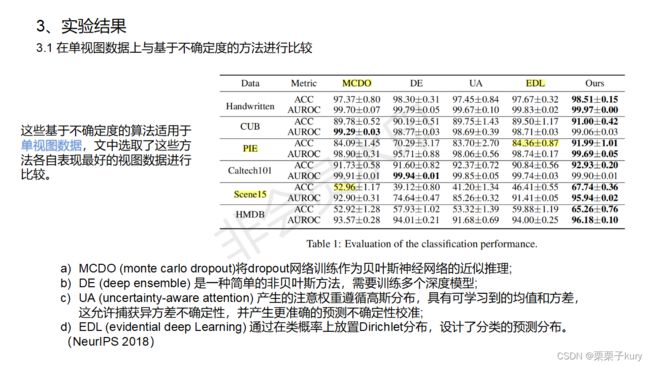
3、实验结果
- 本文提出了一种可信多视图分类(Trusted multi-view classification)算法,该算法基于Dempster-Shafer证据理论,可以对多视图数据产生可信的分类决策。
- 该算法侧重于通过融合多个视图的不确定性来进行决策,可以准确地识别对决策有风险的视图,并在最终决策中利用信息性视图。
- 本文模型可以在进行最终分类时产生当前决策的不确定性,提供可解释性。
- 实证结果验证了该算法在分类精度和分布外识别方面的有效性。