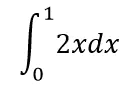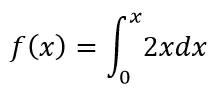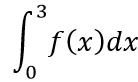Python基础学习（三）

Python基础学习（三）

1.文件操作

1.1打开文件

   通过open()函数可以按指定模式打开指定文件并创建文件对象，例如：文件对象名=open（文件名[,打开方式[,缓冲区]）
   其中，文件名指定了被打开的文件名称，如果要打开的文件不在当前目录中，还需指定完整路径。注意，文件路径中的\要写成\\。打开方式指定了打开文件后的处理方式，例如：只读，只写，追加等，缓冲区指定了读写文件的缓冲模式，数值0表示不缓冲，数值1表示缓冲，如大于1表示缓冲区大小，默认值是缓冲模式。

# 1.打开文件
file = open("read.txt", "w") # 以只写方式打开文件。如果文件存在会被覆盖。如果文件不存在，创建新文件

# 2. 写入文件
file.write("vvcat")

# 3.关闭文件
file.close()

1.2操作文件的函数/方法

函数/方法	说明
open	打开文件，并且返回文件操作对象
read	将文件内容读取到内存
write	将指定内容写入文件
close	关闭文件

· open 函数负责打开文件，并且返回文件对象
  如果文件存在，返回 文件操作对象；
  如果文件不存在，会抛出异常。
· read 方法可以一次性 读入 并 返回文件的所有内容
· close 方法负责关闭文件
  如果忘记关闭文件，会造成系统资源消耗，而且会影响到后续对文件的访问。

1.3文件管理方法

函数名	说明
os.listdir(“目录名”)	返回指定目录下的文件和目录列表
os.rename(“当前文件名”,“新文件名”)	文件重命名
os.mkdir(“新目录名”)	在当前目录创建目录
os.getcwd()	显示当前的工作目录
os.rmdir(“待删除目录名”)	删除目录时要先删除目录中的所有内容，然后才能删除目录

2.Sympy工具库在数学方面的应用

2.1常用模块如下：

abc:符号变量模块;
calculus:积分相关方法;
core:基本的加、乘、指数运算等;
discrete:离散数学;
functions:基本的函数和特殊函数;
galgebra:几何代数;
geometry:几何实体;
integrals:符号积分;
interactive:交互会话(如IPython);
logic:布尔代数和定理证明;
matrices:线性代数和矩阵;
ntheory:数论函数;
physics:物理学;
plotting:用 Pyglet进行二维和三维的画图;
polys:多项式代数和因式分解;
printing:漂亮的打印和代码生成;
series:级数;
simplify:化简符号表达式;
solvers:方程求解;
stats:统计学.

这些模块可以满足常用的计算需求，如代数、积分、离散数学、量子物理、画图与打印等，计算结果还可以输出为LaTeX或其他格式。

针对一些模块进行简要描述：

一.微积分模块(sympy.integrals)
   微积分模块支持大量的基础与高级微积分运算功能.例如,支持导数、积分、级数展开、微分方程以及有限差分方程. SymPy还支持积分变换;在微分中,还支持数值微分、复合导数和分数阶导数

二.离散数学模块(sympy.discrete）
   离散数学指变量特征是离散的数学分支,与连续变量的数学(微积分)区分开来.它主要处理整数、图形以及逻辑学中的问题.这个模块对二项式系数、乘积与求和运算有完整的支持

三.方程求解模块(sympy.solvers)
   求解器(solvers)是SymPy 中求方程解的模块.这个模块具有解复数多项式以及多项式组的能力.它可以解代数方程、常微分方程、偏微分方程和差分方程

四.矩阵模块(sympy.matrices)
   SymPy具有强大的矩阵与行列式计算的功能．矩阵属于线性代数的分支.SymPy支持矩阵创建，如全0矩阵、全1矩阵、随机矩阵以及矩阵运算.它还支持一些特殊函数，如计算黑塞矩阵(Hessian matrix)的函数、一组向量的格拉姆-施密特(Gram-Schmidt)正交化函数、朗斯基 (Wronskian)行列式计算的函数等。另外，SymPy还支持特征值和特征向量的计算、矩阵的转置以及矩阵与行列式求解.还支持因式分解算法等.在计算中,还有零空间(null space)计算,行列式、代数余子式展开工具以及伴随矩阵

五.物理学模块(sympy.physics)
   SymPy有一个模块可以解决物理学问题.它支持力学功能，包括经典力学与量子力学以及高能物理学。它还支持一维空间与三维空间的泡利代数与量子谐振子,支持光学相关的功能。它还有一个独立的模块将物理单位集成到SymPy 里，用户可以选择相应的物理单位完成计算和单位转换

六.统计学模块(sympy.stats)
   SymPy的统计学模块支持数学计算中涉及的许多统计函数。除了常见的连续与离散随机分布函数，它还支持符号概率相关功。SymPy库中的随机分布函数都支持随机数生成功能

2.2符号运算基础知识

   借助sympy.symbols()方法，我们可以声明一些变量，从而获得数学表达式和多项式的变量，相当于f(x)中的x变量。

求方程的解

# import sympy 
from sympy import *

# Use sympy.symbols() method 
x= symbols('x') 
x = 2
gfg = x**2 + 4 * x + 4
  
print(gfg)##16

在构建多个变量时，中间以空格分隔,比如：

x,y=symbols('x y')

在符号计算中，使用evalf()或n()方法来获得任何对象的浮点近似值，默认的精度是小数点后15位，而且可以通过调整参数改成任何想要的精度。

#--------多项式求解--------
#定义变量
x=Symbol('x')
fx=6*x+5
#使用evalf函数传值
y1=fx.evalf(subs={x:6})##相当于将x=6代入上面的式子
print(y1)##41.0000000000000

#多元表达式
x=sympy.Symbol('x')
y=sympy.Symbol('y')
fx=x*x+y*y
result=fx.evalf(subs={x:3,y:4})
print(result)##25.0000000000000

用 sympy.solve() 函数来解单一方程的调用方式可以表示为 sympy.solve(表达式,符号) 。下面的代码演示了怎样解x*3+9=0这个方程。

#解方程 有限解
#定义变量
x=Symbol('x')
fx=x*3+9
#可求解直接给出解向量
print(solve(fx,x))##[-3]

sympy.solve()函数报错的解决方法

求解方程组：
x+y=3, x-y=-5

x=Symbol('x')
y=Symbol('y')
f1=x+y-3
f2=x-y+5
intr=solve([f1,f2],[x,y])
print(intr)##{x: -1, y: 4}

#解方程无穷多解
#定义变量
x=Symbol('x')
y=Symbol('y')
fx=x*3+y**2
#得到是x与y的关系式，
print(solve(fx,x,y))##[(-y**2/3, y)]

求和：

#定义变量
n=Symbol('n')
f=2*n
#前面参数放函数，后面放变量的变化范围
s=summation(f,(n,1,100))
print(s)##10100

求极限（注意，math包中sin和很多数学函数会报错，要用sympy中的，无穷大用 sympy.oo 表示）

#求极限使用limit方法
#定义变量与函数
x=Symbol('x')
f=(1+x)**(1/x)
#三个参数是 函数，变量，趋向值
lim=limit(f,x,0)
print(lim)##E

求导：

#求导使用diff方法
x=Symbol('x')
f1=2*x**4+3*x+6
#参数是函数与变量
f1_=diff(f,x)
print(f1_)

#求偏导
y=Symbol('y')
f2=2*x**2+3*y**4+2*y
#对x，y分别求导，即偏导
f2_x=diff(f2,x)
f2_y=diff(f2,y)
print(f2_x)
print(f2_y)

输出结果如下：

(x + 1)**(1/x)*(1/(x*(x + 1)) - log(x + 1)/x**2)
4*x
12*y**3 + 2

求定积分

#求定积分用 integrate方法
x=Symbol('x')
f=2*x
#参数传入 函数，积分变量和范围
result=integrate(f,(x,0,1))
print(result)##1

多重积分：

#求多重积分，先求里面的积分，再求外面的
x,t=symbols('x t')
f1=2*t
f2=integrate(f1,(t,0,x))
result=integrate(f2,(x,0,3))
print(result)##9

数学符号补充：

 
#数学符合
#虚数单位i
sympy.I
#自然对数低e
sympy.E
#无穷大
sympy.oo
#圆周率
sympy.pi
#求n次方根
sympy.root(8,3)
#求对数
sympy.log(1024,2)
#求阶乘
sympy.factorial(4)
#三角函数
sympy.sin(sympy.pi)
sympy.tan(sympy.pi/4)
sympy.cos(sympy.pi/2)

求下列微分方程的解：
初值问题：y’‘-5y’+6y=0,y(0)=1,y’(0)=0

x=symbols('x'); y=symbols('y',cls=Function)
eq1=diff(y(x),x,2)-5*diff(y(x),x)+6*y(x)#先构造微分方程
print("初值问题的解为：{}".format(dsolve(eq1,y(x),ics={y(0):1,diff(y(x),x).subs(x,0):0})))#diff函数求导
#初值问题和边值问题格式相同