机器学习之回归算法

机器学习之回归算法

1.线性回归

1.1线性回归原理

回归问题：
目标值----连续性的数据
应用场景：
房价预测、销售额度预测等等
定义：
线性回归是利用回归方程（函数）对一个或多个自变量（特征量）和因变量（目标值）之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归，大于一个自变量情况的叫做多元回归。
其表达形式为y = w'x+e，e为误差服从均值为0的正态分布，也称为偏置量。
回归模型分为两种：
（1）线性：两个变量之间的关系是一次函数关系的——图象是直线，叫做线性。（w（参数）或者x的次数是一次）
注意：题目的线性是指广义的线性，也就是数据与数据之间的关系。
（2）非线性：两个变量之间的关系不是一次函数关系的——图象不是直线，叫做非线性。

线性关系一定是线性模型
线性模型不一定是线性关系。

1.2线性回归的损失与优化原理

目标：求模型参数 ，优化损失，使损失最小。
线性回归的损失与优化

1.3线性回归API

1.4波士顿房价预测（案例）

项目介绍：最终目的：预测房价

流程：
（1）获取数据集
（2）划分数据集
（3）特征工程：
   因为有些特征值的数据有些比较大，有些比较小，所以需要进行无量纲化处理（用标准化）。
（4）预估器流程：fit->模型
（5）模型评估
回归的性能评估：`均方误差（MSE）

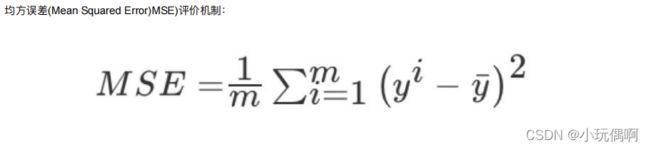
！！！！！！！！！！！上述不是减平均值，而是预测值减真实值。

`sklearn.metrics.mean_squared_error(y_test,y_pred)
返回的是浮点数
正规方程的优化方法：

from sklearn.datasets import load_boston##导入波士顿数据集
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression,SGDRegressor,RidgeCV,Ridge
from sklearn.metrics import mean_squared_error
import warnings
warnings.filterwarnings("ignore")

def linear_model1():
    # 1.获取数据
    boston=load_boston()
    # 2.划分数据
    x_train,x_test,y_train,y_test=train_test_split(boston.data,boston.target,random_state=22)##最后一个参数保持数据一致，返回数据顺序不可以调换
    # 3.特征工程--标准化
    transfer=StandardScaler()
    x_train=transfer.fit_transform(x_train)##训练集
    x_test=transfer.fit_transform(x_test)##测试集
    # 4.机器学习---线性回归 预估器
    estimator=LinearRegression()
    estimator.fit(x_train,y_train)
    #得出模型
    print("正规方程的偏置是：\n",estimator.intercept_)
    print("正规方程的系数是：\n",estimator.coef_)

    # 5. 模型评估
    ## 5.1 预测值
    y_pre=estimator.predict(x_test)
    print("预测房价:\n",y_pre)
    ## 5.2 均方误差
    ret=mean_squared_error(y_test,y_pre)
    print("均方误差：\n",ret)

linear_model1()

梯度下降的优化方法：

def linear_model2():
    # 1.获取数据
    boston=load_boston()
    # 2.划分数据
    x_train,x_test,y_train,y_test=train_test_split(boston.data,boston.target,random_state=22)
    # 3.特征工程--标准化
    transfer=StandardScaler()
    x_train=transfer.fit_transform(x_train)
    x_test=transfer.fit_transform(x_test)
    # 4.机器学习---线性回归
    #estimator=SGDRegressor(max_iter=1000,learning_rate="constant",eta0=0.001)
    estimator=SGDRegressor(max_iter=1000)#迭代次数
    estimator.fit(x_train,y_train)

    print("梯度下降的偏置是：\n",estimator.intercept_)
    print("梯度下降的系数是：\n",estimator.coef_)

    # 5. 模型评估
    ## 5.1 预测值
    y_pre=estimator.predict(x_test)
    print("预测房价:\n",y_pre)
    ## 5.2 均方误差
    ret=mean_squared_error(y_test,y_pre)
    print("均方误差：\n",ret)
linear_model2()

梯度下降可以通过调参来减小均方误差

梯度下降	正规方程
需要选择学习率	不需要
需要迭代求解	一次运算得出
特征量较大可以使用	需要计算方程，时间复杂度高

• 选择
  • 小规模数据：（小于10万条）
    • LinearRegression(不能解决拟合问题） 用的很少
    • 岭回归
  • 大规模数据：SGDRegressor
    拓展：优化方法：GD（传统梯度下降）、SGD（上面用到的梯度下降）、SAG(岭回归和逻辑回归会用)

2.欠拟合和过拟合

欠拟合：训练集上表现不好，测试集上表现不好，学习特征太少。
解决：增加数据的特征数量。
过拟合：训练集上表现的好，测试集上表现不好，学习特征太多。
解决：正则化（L2正则化更常用）
欠拟合和过拟合

3.岭回归（带L2正则化的线性回归）

API介绍：alpha=惩罚项系数，solver(SAG优化)

正则化力度越大，权重系数越小。
岭回归对波士顿房价进行预测：

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression,SGDRegressor,RidgeCV,Ridge
from sklearn.metrics import mean_squared_error
import joblib
import warnings
warnings.filterwarnings("ignore")

def linear_model3():
    # 1.获取数据
    boston=load_boston()
    # 2.划分数据集
    x_train,x_test,y_train,y_test=train_test_split(boston.data,boston.target,random_state=22)
    # 3.特征工程--标准化
    transfer=StandardScaler()
    x_train=transfer.fit_transform(x_train)
    x_test=transfer.fit_transform(x_test)
    # 4.机器学习---线性回归 预估器
    estimator=Ridge(alpha=1.0)
    estimator.fit(x_train,y_train)
   
    print("岭回归的偏置是：\n",estimator.intercept_)
    print("岭回归的系数是：\n",estimator.coef_)
  
    # 5. 模型评估
    ## 5.1 预测值
    y_pre=estimator.predict(x_test)
    print("预测房价：\n",y_pre)
    ## 5.2 均方误差
    ret=mean_squared_error(y_test,y_pre)
    print("均方误差：\n",ret)
linear_model3()