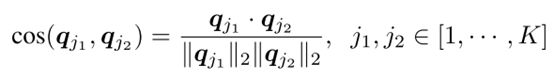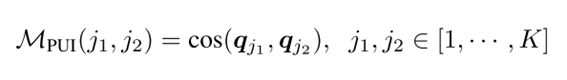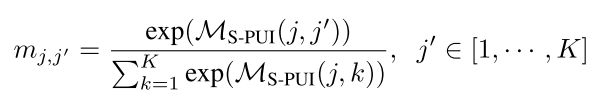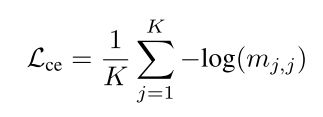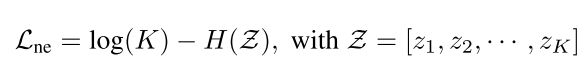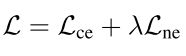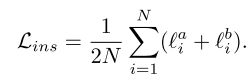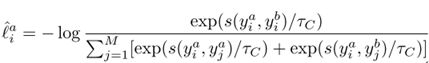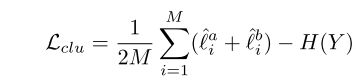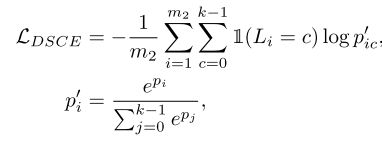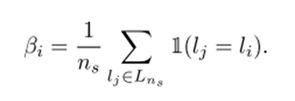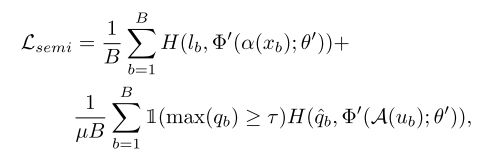深度聚类部分简述

摘要

  传统的K-means聚类算法，对于维度高、数量级大的数据集不能很好地执行聚类，甚至无法得到有效的聚类效果，在实际场景中难以应用。针对上述问题，2016年Deep Embedding Clustering (DEC)深度聚类算法被提出，从而引领了深度聚类算法研究的热潮。近两年的研究采用了自监督的学习策略，本文主要记录自己最近阅读的三篇有关深度聚类的文章。

（PICA）Deep Semantic Clustering by Partition Confidence Maximisation

摘要

作者认为，现有的深度聚类方法通常依赖于基于样本间关系或自估计伪标记的局部学习约束方法，这不可避免地受到的分布在邻域的误差影响，并在训练过程中产生误差传播的累积问题。自然图像中普遍存在类内视觉差异和类间相似，大多数来自相同语义类的样本仍会共享高比例的视觉信息。在这种情况下，作者基于观察到将来自相同语义类别的样本分配到不同的聚类中会降低聚类内部的紧凑性和簇间的多样性。如何提高这些聚类的语义合理性仍然是一个需要解决的问题。本文建议通过从所有可能的分配中学习最可信的聚类解决方案来解决这个问题，本文引入了一种名为 PartItion Confidence maximization (PICA) 的新型深度聚类方法。该模型主要思想为：通过最大化聚类方法的global分割置信度来学习语义上最合理的数据分离，其能够使所有cluster都能一对一映射到ground truth类别。上述内容通过引入可微划分不确定性指标（执行特征表示学习和聚类分配时模型分离一组目标图像的置信度）及其随机近似并提出基于最小化不确定性指标的目标损失函数实现。

介绍

该模型主要包含两个部分进行端到端学习：

1. 特征提取器 

2. 分类器

对于N张图片，模型预测的cluster分配矩阵可以表示为P=[p1,……pn]∈RK*N，其中pi为第i个样本的cluster分布。P的第 j 行qj可以表示第j个cluster包含每个图片的概率，作者将其称为cluster-wise Assignment Statistics Vector (ASV)。

qj=p1,j……pN,j∈R1*N,j∈[1,……k]

理想状态下应该是one-hot向量，即每个样本只属于最可能的（most confident）一个cluster。因此作者构建partition uncertainty index为ASV之间的余弦相似度矩阵MPUI（j1,j2）

 

。

具体来说两个不同的ASV 应该是正交的（余弦相似度为0），在最坏的聚类情况下，结果为1（例如均匀分布），对于中间的任何情况，ASV两个簇的余弦相似度将在 0（最可信）到 1（最不可信）之间变化。

 

 

对于任何两个不同的cluster，要最小化其对应ASV向量的余弦相似度, 因此作者通过softmax实现上述需求。则网络只需最大化mj,j'。

作者构建类似交叉熵的loss对其进行优化。

另外，在聚类中，通常出现将大部分样本分配到少数的聚类中。为了避免这种情况，本文引入了一个额外的约束，使簇大小分布的负熵最小化。

则PICA的总loss函数如下

总结

  本文采用余弦相似度计算ASV和PUI的代码和思想，本文引入了一个额外的约束，使簇大小分布的负熵最小化。在好几篇文章中都有看到这样的处理机制，应该可以作为聚类算法优化的一个突破点。

（CC）Contrastive Clustering

摘要

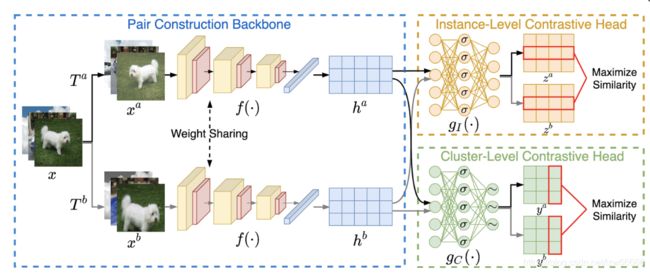
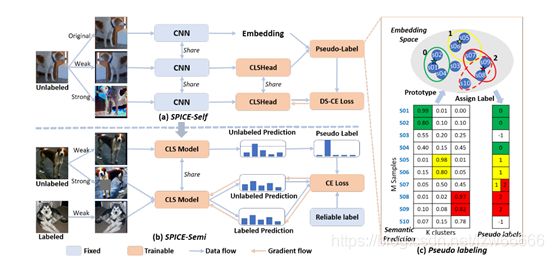
现有的大部分深度聚类(Deep Clustering)算法需要迭代进行表示学习和聚类这两个过程，利用聚类结果来优化表示，再对更优的表示进行聚类。此类方法主要存在以下两个缺陷，一是迭代优化的过程中容易出现误差累计，二是聚类过程通常采用k-means等需要全局相似性信息的算法，使得需要数据全部准备好后才能进行聚类，故面临不能处理在线数据的局限性。针对上述问题，本文提出了一种基于对比学习的聚类算法，其同时进行表示学习和聚类分析，且能实现流式数据聚类。本文基于“标签即表示”的思想，将聚类任务统一到表示学习框架下，对每个样本学习其聚类软标签作为特征表示。具体而言，揭示数据特征矩阵的行和列事实上分别对应实例和类别的表示(左图)。也即，特征矩阵的列是一.种特殊的类别表示，其对应某一实例属 于某一类别的概率。基于此，本文提出同时在特征矩阵的行空间与列空间，即实例级别和类别级别，进行对比学习即可进行聚类。

介绍

如上图所示，模型包括三个主要部分：1. pair construction backbone(PCB) 2. instance-level contrastive head (ICH) 3. cluster-level contrastive head (CCH)。简单来说，PCB通过实例对进行对比并从增强样本中提取特征，之后ICH和CCH分别从行和列分别进行对比学习。

PCB：完成利用数据増广构造用于对比学习的正负样本対，通过骨干网络提取特征。

ICH：作者并没有直接使用特征计算对比学习loss，而是构建两层非线性MLP ，将特征矩阵映射到子空间z,则其loss可以定义为：

其中τI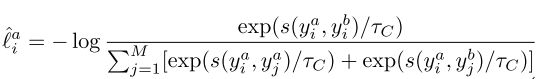是实例层次的temperature变量，实例样本对相似度是通过余弦距离来衡量的。s(zia,zib)为余弦相距离。则所有样本的总loss为：

 

CCH：当数据样本被映射到与cluster数量相同的空间时，数据特征的每一维可以看作该样本属于该cluster的概率。类似ICH，构建两层非线性MLP g c (),将特征矩阵映射到M维(cluster数量)空间y。定义Ya∈RN*M（N为batchsize， M为cluster数量）为一个mini-batch数据经历CCH的输出。由于一个样本只属于一个cluster，因此Ya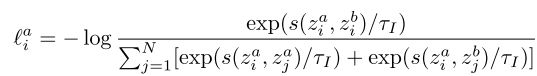 的每一行趋向于one-hot，每一列代表每个cluster的分配结果，即每一列都需要尽量不同。loss可以定义为：

 

其中τc是实例层次的temperature变量，集群样本对相似度是通过余弦距离来衡量的。s(z_i^a,z_i^b)为余弦相距离。则所有样本的针对所有增强的集群层次总loss如下：

其中H(Y)为cluster分配概率的信息熵, 目的是避免网络将所有实例都分配到一个cluster。

最终CCzongloss为ICH部分的loss与CCH部分的loss相加，即为：

 

总结

  本文提出了名为对比聚类(CC)的在线聚类方法，它执行实例级和集群级的对比学习。具体地说，对于给定的数据集，通过数据扩充来构造正实例对和负实例对，然后投影到特征空间中。通过同时优化实例级和集群级的对比损失，该模型以端到端方式联合学习表示和集群分配。为当前的深度聚类研究提供了一种新的见解，即实例表示和聚类类别预测分别对应于可学习特征矩阵的行和列。

 

 

SPICE: Semantic Pseudo-labeling for Image Clustering

摘要

  针对SCAN算法容易出现语义不一致的最近邻样本，导致聚类结果产生误差累积的问题，本文提出了一种基于图像语义伪标签的图像聚类框架（SPICE），他指出SCAN存在以下问题：在实际的样本空间中，并不是所有样本的最近邻都具有相同的语义，比如当样本位于不同簇的边界时，这样的问题会变得更加严重，从而导致最终的聚类结果产生误差累积。SPICE的结构包括三个训练阶段：1、预训练一个无监督表示学习模型（改编自SCAN中的方法）。2、对预训练模型的CNN骨架进行冻结，从而通过SPICE-Self输出特征和标签。3、从SPICE-Self聚类结果中选出可信的标签，用半监督学习的方法重新分类。

 

介绍

SPICE-Self旨在基于无监督预训练模型提取到的特征进行分类，它包括三个分支：第一个分支以原始图像为输入，输出嵌入特征(embedding features)；第二个分支以弱变换图像为输入，输出语义标签(semantic labels)；第三个分支以强变换图像为输入，输出聚类标签(cluster labels)。利用基于语义相似度的伪标记(psedo-label)算法，使用前两个分支的输出结果生成伪标签，再用伪标签对第三个分支进行监督。在实践中，SPICE-Self只需要训练第三分支的轻量级分类头。

 

 

第一步：用预训练的CNN输出嵌入特征M∈RM*D , 在CNN后接一个多层感知机聚类头（CLSHead），预测弱变换后样本属于某一类的概率P∈RM*K,（M为batch大小，D为特征维数，K为聚类数）。第二步，相比SCAN简单地选取每个样本的最近邻语义样本处理方法，本文提出在一个batchsize里面选取其中大于给定阈值的最自信的前个样本作为伪标签。以它们的嵌入特征的均值作为聚类中心。然后将聚类中心最近的n=M/k个样本作为赋予该类的伪标签。 第三步：对样本作强变换，定义DSCE损失进行训练。

DSCE：

 

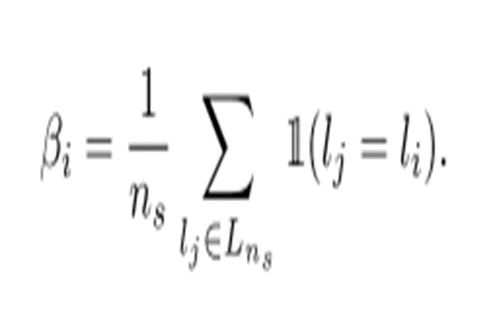SPICE-Semi从SPICE-Self得到了样本、聚类结果、嵌入特征的三元组( xi , li , fi )，对于每个样本xi ，根据余弦相似性从嵌入特征空间选取相邻的ns个样本，计算这些样本中与xi 属于同一类的比例。比例大于某个阈值时，认为样本xi 的类别分配是可信的。样本 xi 的局部一致性Bi定义为：

 

训练部分，这里使用了FixMatch方法。对有标签数据，计算CLS Model预测结果与标签的交叉熵；对于无标签数据，计算使用CLS Model对强变换的预测结果与弱变换预测的伪标签的交叉熵。损失函数是二者之和。总损失为：

总结

  本文主要是解决SCAN算法中最近邻样本容易出现不一致语义的问题，并且在实验效果上要比SCAN算法强很多。其中半监督部分结合了半监督算法FixMatch，通过弱变换这一支确定伪标签，强变换这一支输出的特征与伪标签求交叉熵进行训练。