机器学习:KNN算法
目录
关于KNN算法
原理
一般流程
算法伪代码
关于距离的计算
关于K值的选择
关于KNN算法的优缺点以及适用范围
KNN算法的实现
数据收集与相关处理
KNN核心算法
测试
关于KNN算法
原理
存在一个样本数据集合,也称作训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每一数据与所属分类的对应关系。输入没有标签的新数据后,将新数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本几种特征最相似数据(最近邻)的分类标签。 ——《机器学习实战》
一般流程
1.收集数据
2.准备数据:距离计算所需要的数值,最好是结构化的数据格式
3.分析数据
4.测试算法:计算错误率
5.使用算法:首先需要输入样本数据和结构化的输出结果,然后运行KNN算法判定输入数据属于哪个分类,最后应用对计算出的分类执行后续的处理。
算法伪代码
对未知类别属性的数据集中的每个点依次执行以下操作:
1.计算已知类别数据集中的点与当前点之间的距离
2.按距离递增次序排序
3.选取与当前点距离最小的k个点
4.确定前k个点所在类别的出现频率
5.返回前k个点出现频率最高的类别作为当前点的预测分类
根据伪代码,我们不难发现,在KNN算法中影响很大的两个因素,距离和k值。
关于距离的计算
在KNN算法中,通常使用欧氏距离公式进行计算:
![]()
通过该公式简单粗暴地计算预测点与所有点之间的距离。
关于K值的选择
| K值 | 影响 |
|---|---|
| 过大 |
预测标签比较稳定,可能过平滑,容易欠拟合
|
| 过小 |
预测的标签比较容易受到样本的影响,容易过拟合
|
我们通常可以使用交叉验证的方法来确定k值的大小,从选取一个较小的K值开始,不断增加K的值,然后计算验证集合的方差,最终找到一个比较合适的K值。
关于KNN算法的优缺点以及适用范围
优点:精度高、对异常值不敏感、无数据输入假定
缺点:计算复杂度高、空间复杂度高
适用数据范围:数值型和标称型
KNN算法的实现
数据收集与相关处理
数据集收集
| 在宿舍所占日常时间百分比 | 打游戏所占时间百分比 | 是否为计算机院学生 |
|---|---|---|
| 60 | 10 | 1 |
| 50 | 20 | 1 |
| 74 | 10 | 1 |
| 88 | 60 | 0 |
| 32 | 64 | 0 |
| 45 | 61 | 0 |
| 23 | 12 | 0 |
| 75 | 5 | 1 |
| 64 | 76 | 0 |
| 17 | 65 | 0 |
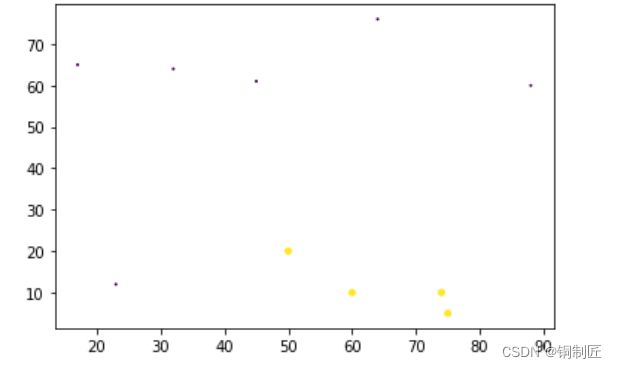
数据可视化
def paint(group,labels):
fig=plt.figure()
ax=fig.add_subplot(111)
x=group[:,0]
y=group[:,1]
ax.scatter(x,y,15.0*np.array(labels)+1,15.0*np.array(labels)+1)
plt.show()
KNN核心算法
def KNN(inX, dataSet, labels, k):
dataSetSize = dataSet.shape[0]
diffMat = np.tile(inX, (dataSetSize, 1)) - dataSet
sqDiffMat = diffMat ** 2
sqDistances = sqDiffMat.sum(axis=1)
distances = sqDistances ** 0.5
sortedDistIndices = distances.argsort()
classCount = {}
for i in range(k):
voteIlabel = labels[sortedDistIndices[i]]
classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
sortedClassCount = sorted(classCount.items(),
key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]测试
if __name__=='__main__':
group_train,labels_train=DataSet()
paint(group_train,labels_train)
group_test=np.array([[21,3],[14,72],[84,41],[33,43]])
for i in range(len(group_test)):
label_test=KNN(group_test[i],group_train,labels_train,3)
print('在宿舍所占日常时间百分比:%d 打游戏所占时间百分比: %d 是否为计算机院学生:%d'
%(group_test[i][0],group_test[i][1],label_test))