预测房价：回归问题

目录

分类问题与回归问题

数据集

数据标准化

构建网络

采用K折验证来验证你的方法

K折交叉验证

  小结

---

分类问题与回归问题

        分类问题与回归问题都是机器学习常见的问题，分类问题的目标是预测数据点对应的单一离散标签，而回归问题预测的是连续值而不是离散的标签，eg:根据气象数据预测明天的气温。

数据集

        采用20世纪70年代，波士顿房屋价格数据集，共506个样本，训练样本404个，预测样本102个，每个样本都有13个特征，人均犯罪率、房地产税率、住宅房间数等。

#波士顿房价数据
from keras.datasets import boston_housing
(train_data,train_targets),(test_data,test_targets) = boston_housing.load_data()
#train_data.shape = (404,13)训练数据维度
#test_data.shape = (102,13)测试数据维度
print(train_data[0])

[  1.23247   0.        8.14      0.        0.538     6.142    91.7
   3.9769    4.      307.       21.      396.9      18.72   ]

        显然，不同特征的数据差距很大，对数据的学习可能会有一定的困难，所以需要进行数据标准化，即，输入数据的每个特征（列）都减去平均值，除以标准差，这样得到的特征平均值为0，标准差为1。

数据标准化

#数据标准化
mean = train_data.mean(axis=0)
train_data -= mean
std = train_data.std(axis=0)
train_data /= std

#训练数据和测试数据标准化用到的均值和标准差都是训练数据得到的
test_data -= mean
test_data /= std

        训练数据和测试数据的均值和标准差都是在训练数据中得到的，工作过程中，不能在测试数据中得到任何计算结果，标准化也不行。

构建网络

        由于数据量较少，使用较小的网络就可以完成，此处使用一个三层网络架构，一般来说，数据越少，过拟合情况就会越严重，使用较小的网络可以降低过拟合。

#构建网络
from keras. import models
from keras import layers

def build_model():
    model = models.Sequential()
    model.add(layers.Dense(64,activation='relu',input_shape(train_data.shape[1],)))
    model.add(layers.Dense(64,activation="relu"))
    model.add(layers.Dense(1))
    model.compile(opyimizer='rmsprop',loss='mse',metrics=["mae"])
    return model

         显然网络的最后一个单元只有一个输出单元，而且没有激活函数，是一个线性层。这是标量回归的典型设置（标量回归是预测单一连续值的回归）。如果最后一层使用的逻辑回归激活函数sigmoid，那么网络只能学会预测0~1范围的值，如果最后一层是纯线性的，网络可以预测任意范围的值。

        对于网络的编译，逻辑回归最常用的损失函数就是mse损失函数，即均方差；训练过程中，还通过metrics监控一个新指标，mae平均绝对误差，它是预测试和目标值之差的绝对值。

采用K折验证来验证你的方法

        由于总数据量有限，将数据划分为训练集和验证集后，验证集的数据量会很小，那么验证集的训练结果就会有很大波动。也就是说，验证集的划分方式可能会造成验证分数上很大的方差，这样就不能对模型进行准确评估，最好的方法就是使用K折交叉验证。

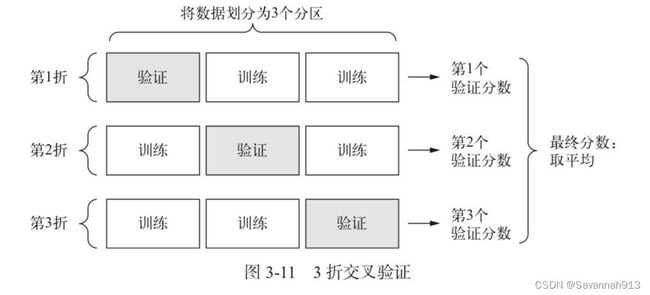
K折交叉验证

        将数据划分为K个分区（通常是4，5），实例化K个相同的模型，每个模型在K-1个分区上进行训练，在剩下的一个模型上进行评估，模型的验证集分数是这K个验证分数的平均值。

#构建网络
from keras import models
from keras import layers

def build_model():
    model = models.Sequential()
    model.add(layers.Dense(64,activation='relu',input_shape=(train_data.shape[1],)))
    model.add(layers.Dense(64,activation="relu"))
    model.add(layers.Dense(1))
    model.compile(optimizer='rmsprop',loss='mse',metrics=["mae"])
    return model

#采用K折验证来验证你的方法
import numpy as np

k =4
num_val_samples = len(train_data)//k
num_epochs = 500
all_mae_histories = []
for i in range(k):
    #准备验证集第K个分区的数据
    print("processing fold#",i)
    val_data = train_data[i*num_val_samples:(i+1)*num_val_samples]
    val_targets = train_targets[i*num_val_samples:(i+1)*num_val_samples]
    
    #准备训练集数据，除验证集之外的其他所有数据
    partial_train_data = np.concatenate(
        [train_data[:i*num_val_samples],train_data[(i+1)*num_val_samples:]],
        axis = 0
    )
    partial_train_targets = np.concatenate(
        [train_targets[:i*num_val_samples],train_targets[(i+1)*num_val_samples:]],
        axis = 0
    )
    
    #构建模型（已编译）
    model = build_model()
    history = model.fit(
        partial_train_data,
        partial_train_targets,
        epochs=num_epochs,
        batch_size=1,
        validation_data = (val_data,val_targets)
    )
    mae_history = history.history['val_mean_absolute_error']
    all_mae_histories.append(mae_history)

#计算所有轮次的K折验证分数
average_mae_history = [
    np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)
]

import matplotlib.pyplot as plt
#绘制验证集分数
plt.plot(range(1,len(average_mae_history)+1),average_mae_history)
plt.xlabel("Epochs")
plt.ylabel("Validation MAE")
plt.show()

 

 对于上述结果，显然，纵轴范围很大，方差较大，且主要体现在前十个数据点上。

删除前十个数据点，将每个数据点替换为前面数据点的指数移动平均值，以得到光滑的曲线。

def smooth_curve(points,factor=0.9):
    smoothed_points = []
    for point in points:
        if smoothed_points:
            previous = smoothed_points[-1]#存放前面数据点
            smoothed_points.append( previous*factor + point*(1-factor) )
        else:
            smoothed_points.append(point)
    return smoothed_points
#删除前十个数据点
smooth_mae_history = smooth_curve(average_mae_history[10:])
plt.plot(range(1,len(smooth_mae_history)+1),smooth_mae_history)
plt.xlabel("Epochs")
plt.ylabel("Validation MAE")
plt.show()

 

  小结

 ①回归问题与分类问题使用的损失函数不同，分类问题常用的损失函数是交叉熵，而回归问题常用的损失函数是均方误差（MSE）。

② 回归问题与分类问题使用的评估指标不同，分类问题常用的评估指标是准确率Accuracy，而回归问题常用的评估指标是平均绝对误差（MAE）。

③如果输入的特征具有不同的取值范围，应该先进行预处理，对每个特征单独进行缩放。

④当可用数据较少时，使用K折验证可以很好地评估模型，最好使用隐藏层较少（通常一两个）的小型网络，避免严重的过拟合。